基于流固耦合钻柱系统动力学模拟

王荣鹏, 宋桂秋, 周世华

(东北大学 机械工程与自动化学院, 辽宁 沈阳 110819)

深孔钻柱系统主要用于煤炭、石油和天然气生产和勘探过程,系统内部诸多因素之间的相互作用较为复杂[1].在钻柱钻进过程中会发生各种振动,尤其是钻柱的横向振动能够引起钻柱部件失效、磨损、钻头损坏、钻速降低,导致钻井效率低下并产生高昂的成本,从而对钻柱系统产生重大的不利影响.因此研究钻柱系统的横向振动特性,对于降低成本、提高效率具有重要的现实意义[2].目前国内外学者对钻柱系统研究作出了许多贡献:刘永升等[3]建立了斜直井中钻柱4自由度非线性动态模型,在不同井斜角条件下,对钻柱运动进行了数值模拟研究.王长进等[4]通过实验研究了转速、载荷、钻井液等参数对受压屈曲钻柱旋转运动的影响,分析了钻柱在钻井液中由正向涡动转为自转和反向涡动的耗散能量.王文龙等[5]建立了钻柱纵向振动数学模型,分析了钻柱轴向应力振幅分布曲线和最大轴向应力幅频曲线的特征,及钻井液黏度、激励位移和减振器位置等参数对钻柱轴向应力振幅的影响.王尊策等[6]建立了变截面钻柱的摩擦接触有限元模型,对钻柱的屈曲进行了分析研究.李子丰[7]提出钻柱涡动理论研究需要将钻井液动力润滑学与钻柱动力学相结合.Liu等[8]研究了钻柱的黏滑振动,基于路径跟踪方法对非光滑动力系统进行了数值模拟,重点研究了钻柱的稳态问题.Real等[9]提出了一种用于钻柱扭转动力学的滞后钻头岩石相互作用模型,分析了钻柱系统的非线性扭转振动和稳定性.Kamel等[10]提出了一个轴向和扭转运动耦合的钻柱非线性模型,考虑钻头阻力,采用接触数学模型描述钻头和岩层的相互作用.Liang等[11-13]提出了一种旋转多跨流体输送管道的动力学模型,并对该系统的横向固有频率、共振频率和模态特性进行了研究.Zhang等[14]研究了在超临界流速作用下,黏弹性输流管道在弯曲平衡附近的非线性强迫振动,重点研究了外共振和内共振动力学.Guzek等[15]研究了钻井泥浆流变性对垂直钻头振动的影响,确定了减振的最佳泥浆参数范围.Nandakumar等[16]建立了一个耦合的2自由度模型,研究了钻柱的黏滑振动、旋转、钻头弹跳、螺旋屈曲等现象.Leonov等[17]研究了常微分方程描述的钻井系统的数学模型,在这类系统中可能会出现隐藏振荡等复杂效应,这些影响可能导致钻柱失效和故障.Ritto等[18]提出了钻柱扭转振动的集中参数模型,采用非线性摩擦力矩模拟钻头的相互作用,分析了钻柱扭转黏滑振动不稳定性.Hovda[19]建立了油井钻柱轴向运动的集中参数模型,研究了井下压力和运动的各种重要因素,特别是附加质量、稳态黏滞力的影响.Zhao等[20]采用摩擦模型对摩擦自激振动进行了分析,研究了钻柱在四种接触状态下(黏着、边界润滑、部分流体润滑和全润滑)的轴向黏滑运动.Ghasemloonia等[21]建立了整个钻柱轴向与横向耦合非线性动力学模型,并对其横向不稳定性进行了定性研究.

由文献分析可知,虽然近年来国内外学者对钻柱系统动力学特性进行了一些研究,然而考虑钻柱中流体影响和支撑刚度影响的非线性动力学行为的研究还相对较少.本文建立了钻柱系统流固耦合动力学模型,并用Galerkin方法进行了离散,采用Runge-Kutta积分法求解动力学方程.在其他参数固定的情况下,分别给出了以脉动频率、脉动幅值和质量比为控制参数的耦合系统振动响应的分岔图.通过分岔图、时域图、相图和Poincaré截面图,分析了钻柱系统的非线性动力学行为,为了解深孔钻柱系统复杂的非线性动力学特性提供了依据.

1 系统非线性动力学模型

在钻柱系统中,当钻柱只作轴向进给,可将钻柱简化为输送脉动流体的简支梁,如图1所示.无约束的输送脉动流体的简支梁运动方程由文献[22-24]提出,本文在此运动方程的基础上,考虑了钻柱扶正器对钻柱振动的影响,将扶正器简化为弹簧支撑约束[25],用三次非线性弹簧力Fa(y)和Fb(y)模拟反作用力[26],整理后得到深孔钻柱系统流固耦合运动微分方程:

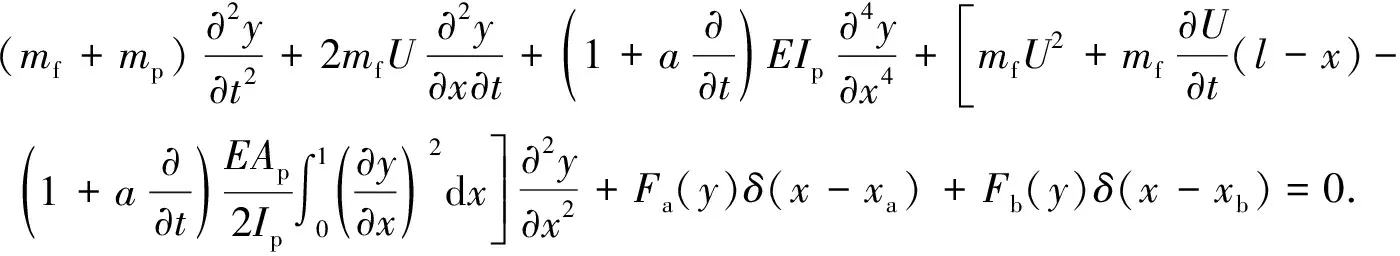
(1)

式中:mf为单位长度流体质量;mp为单位长度钻柱质量;U为流体流速;E为杨氏模量;Ap为钻柱的横截面面积;l为钻柱长度;Ip为钻柱横截面惯量;a为黏弹性阻尼系数;xa和xb分别为沿钻柱轴线距原点的距离;Fa(y)=Kay3,Fb(y)=Kby3，Ka和Kb分别为xa和xb位置处的支撑刚度;x为横坐标;t为时间;y(x,t)为位置x与时间t的横向振动位移函数;δ(·)为Dirac delta函数.

对式(1)引入无量纲变量:

(2)

方程(1)可写为

kbη3δ(ξ-ξb)=0 .

(3)

假设钻柱中流动切削液为周期性脉动流,即无量纲流速为

u=u0(1+μsinωτ) .

(4)

式中:u0为平均流速;μ为脉动幅值;ω为脉动频率.

图1 具有运动约束两端铰支钻柱模型Fig.1 A drilling string model with motion constraints hinged at both ends

2 运动方程的Galerkin离散化

利用Galerkin方法对无量纲化的高阶非线性偏微分方程(1)离散化并降阶化为低次的常微分方程组.假设任意点无量纲位移作如下形式的Galerkin展开式:

(5)

式中:ξ为广义坐标;τ为时间;η(ξ,τ)为任意点ξ无量纲位移;φr(ξ)为正交模态函数;qr(τ)为关于时间的未知广义坐标;N为截断项数.将式(5)代入式(3)中,在[0,1]区间关于ξ积分,并利用模态函数正交性,经过整理后得到降阶后的离散化方程为

(6)

式中:C为阻尼矩阵;K为刚度矩阵.由文献[27]可知,对式(5)取前两阶展式,即N=2可得到较高的计算精度.其中，

(7)

(8)

式中:

G(z)=[0 0 -f1-f2]T;

Q(z)=[0 0 -h1-h2]T.

3 仿真结果与数据分析

钻柱系统的模型参数如表1所示.

表1 模型参数

3.1 脉动频率ω的影响

脉动频率对钻柱系统的动力学行为有着重要的影响,图2a给出了支撑刚度系数ka=kb=0时,其他系统参数取固定常数,脉动频率ω在[30,50]范围内,系统响应随脉动频率ω变化的分岔图.图2b为支撑刚度系数ka=2.1×105,kb=1.3×103时,ω在[30,50]范围内,系统响应随脉动频率ω变化的分岔图.图2中A,B,C分别表示周期运动、拟周期运动和混沌运动,纵坐标为钻柱中心位置振动的位移幅值.由图2a可知,ω在[30,33.65]范围内时,系统出现周期运动、拟周期运动和小窗口的混沌运动形式,当ω=32.1时系统出现跳跃间断的非线性现象.图3a,3b,3c为ω=32.71时的时域图、相图和Poincaré截面图,Poincaré截面图为规则几何形状的椭圆,系统为拟周期运动.随着ω逐渐增大,系统演变为短暂的周期2运动,然后当ω在(34.25,42.25)范围内时,系统演变为混沌运动,当ω=35.28时,如图3d,3e,3f所示,Poincaré截面图出现几何分形结构,系统为混沌运动.随着ω的继续增大,即ω在[42.25,50]范围内,系统演变为周期运动状态,出现倍周期倒分岔现象.当ω=42.75时,系统路径倒分岔演变为周期8运动.当ω=43.57时,如图3g,3h,3i所示,Poincaré截面图吸引子为8个点,即周期8运动.在ω=47.85时系统路径出现倒分岔由周期8运动演变为周期4运动,振动形态的周期数成倍的变化,系统路径以倍周期倒分岔的形式由混沌运动过渡到周期运动.

图2 系统响应随脉动频率ω变化的分岔图Fig.2 Bifurcation diagram of system response with pulsating frequencies ω (a)—ka=kb=0; (b)—ka=2.1×105, kb=1.3×103.

由图2b可知,ω在[30,30.96]范围内时,系统为小窗口的周期2运动.随着ω逐渐增大,系统较图2a提前演变为混沌运动.当脉动频率ω在[35.52,37.68]范围内,系统演变为周期运动,周期运动区域较小.当ω继续增大至(37.68,43.52)区间时,系统演变为拟周期运动.随着ω继续增大,当ω在[43.52,50]范围内,系统演变为混沌运动.系统动力学响应丰富,周期运动、拟周期运动、混沌运动交替出现,系统表现出更复杂的动力学行为.支撑刚度系数对系统响应影响显著.

3.2 脉动幅值μ的影响

为了研究脉动幅值μ对钻柱系统振动特性的影响,图4a给出了支撑刚度系数ka=2.1×106,kb=4.5×106,以脉动幅值μ为控制参数在[0.2,0.6]范围内的分岔图.图4b为支撑刚度系数ka=2.1×105,kb=0时,以脉动幅值μ为控制参数在[0.2,0.6]范围内的分岔图.图4中A,B,C分别表示周期运动、拟周期运动和混沌运动.如图4a所示,当μ较小时,即μ在[0.2,0.259]范围内时,系统响应为混沌运动状态,随着μ的逐渐增大,即μ在(0.259,0.275)范围内时,系统进入小窗口的周期运动，随着μ的继续增大，当μ在[0.275，0.389]范围内时，系统响应主要为混沌运动，响应复杂.当μ在[0.304，0.345]范围内时，观察到小窗口的周期运动.随着μ的继续增大，即μ在(0.389，0.581)范围内时，系统出现明显的周期运动和拟周期运动形式.图5a，5b，5c为μ=0.423时的时域图、相图和Poincaré截面图，Poincaré截面图上的点构成一封闭曲线，系统为拟周期运动状态.当μ=0.515时，如图5d，5e，5f所示，时域图呈现周期变化，此时的相图为一封闭曲线，Poincaré截面图上吸引子为孤立的6个点，系统表现为周期6运动.当μ=0.549时系统出现倍周期分岔现象，系统由周期6运动演变为周期12运动.当μ=0.573时系统由周期12运动通过倍周期分岔演变为周期24运动，系统路径以倍周期分岔的形式由周期运动过渡到混沌运动.在脉动幅值μ=0.557，μ=0.568时系统出现跳跃间断的非线性现象.随着μ的继续增大，即μ在[0.581，0.6]范围内时，系统演变为混沌运动，系统振动幅值变大.当μ=0.592时，如图5g，5h，5i所示，系统呈现非周期变化，相对应的Poincaré截面图为无规则散点，系统运动处在混沌状态.系统动力学响应丰富，周期运动、拟周期运动、混沌运动交替出现，系统动态特性较复杂.

图3 不同脉动频率ω下系统动态响应Fig.3 Dynamic response of the system with different pulsating frequencies ω (a)—ω=32.71,时域图; (b)—ω=32.71,相图; (c)—ω=32.71,Poincaré截面图; (d)—ω=35.28,时域图; (e)—ω=35.28,相图; (f)—ω=35.28,Poincaré截面图; (g)—ω=43.57,时域图; (h)—ω=43.57,相图; (i)—ω=43.57,Poincaré截面图.

图4 系统响应随脉动幅值μ变化的分岔图Fig.4 Bifurcation diagram of system response with pulsation amplitude μ (a)—ka=2.1×106, kb=4.5×106; (b)—ka=2.1×105, kb=0.

图5 不同脉动幅值μ下系统动态响应Fig.5 Dynamic response of the system with different pulsation amplitude μ (a)— μ=0.423,时域图; (b)— μ=0.423,相图; (c)— μ=0.423,Poincaré截面图; (d)— μ=0.515,时域图; (e)— μ=0.515,相图; (f)— μ=0.515,Poincaré截面图; (g)— μ=0.592,时域图; (h)— μ=0.592,相图; (i)— μ=0.592,Poincaré截面图.

由图4b可知,当脉动幅值μ较小时,即μ在[0.2,0.262]范围内时,系统出现周期运动、拟周期运动和混沌运动交替形式.在μ=0.218时系统出现跳跃间断的非线性现象.当μ在[0.251,0.262]范围内时,系统出现小窗口的周期运动.随着μ的逐渐增大,即μ在(0.262,0.394)范围内时,系统演变为混沌运动,混沌运动强度也随之增大.随着μ的继续增大,即μ在[0.394,0.6]范围内时,系统主要以周期2运动为主.通过对比图4a和图4b可以发现,选取不同支撑刚度系数,系统响应发生明显变化,系统的跳跃间断现象提前,这主要是由于支撑刚度在一定程度上引起系统固有特性的改变,可见支撑刚度对系统的非线性动力学行为有复杂的影响.

3.3 质量比β的影响

钻柱系统质量比β是评价系统性能的重要参数.在本节中图6a为支撑刚度系数ka=2.6×106,kb=2.1×106时,以质量比β为控制参数在[0.2,0.8]范围内的分岔图.图6b为支撑刚度系数ka=2.6×106,kb=5.6×106时，以质量比β为控制参数在[0.2,0.8]范围内的分岔图.图6中A,B,C分别表示周期运动、拟周期运动和混沌运动.如图6a所示,当β较小时,即β在[0.2,0.261]范围内时,系统响应为周期运动和拟周期运动.图7a,7b,7c为β=0.237时的时域图、相图及Poincaré截面图,此时的相图为一封闭曲线,Poincaré截面图为2个点,系统表现为周期2运动.当β=0.246时,如图7d,7e,7f所示,系统运动为拟周期运动状态.随着β的增大,即β在(0.261,0.354)范围内时,系统响应为混沌运动,混沌运动区域逐渐增大.随着β的继续增大,系统响应出现短暂的周期运动.当β在[0.387,0.456]范围内时,系统响应主要为混沌运动,当β=0.389时,如图7g,7h,7i所示,系统为混沌运动状态.随着β的继续增大,系统响应出现小窗口的周期运动.当β在[0.469,0.727]范围内时,系统演变为混沌运动,混沌区域明显增大.随着β的进一步增大,即β在(0.727,0.8)范围内时,系统演变为周期6运动.

图6 系统响应随质量比β变化的分岔图Fig.6 Bifurcation diagram of system response with mass ratio β (a)— ka=2.6×106, kb=2.1×106; (b)— ka=2.6×106, kb=5.6×106.

图7 不同质量比β下系统动态响应Fig.7 Dynamic response of the system with different mass ratio β (a)—β=0.237,时域图; (b)—β=0.237,相图; (c)—β=0.237,Poincaré截面图; (d)—β=0.246,时域图; (e)—β=0.246,相图; (f)—β=0.246,Poincaré截面图; (g)—β=0.389,时域图; (h)—β=0.389,相图; (i)—β=0.389,Poincaré截面图.

由图6b可知,当β较小时,即β在[0.2,0.326]范围内时,系统响应为周期运动和拟周期运动.随着β的增大,即β在(0.326,0.422)范围内时,系统演变为混沌运动,混沌运动区域逐渐增大.随着β的继续增大,即β在[0.422,0.451]范围内时,系统响应出现小窗口的周期运动.随着β的继续增大,系统返回混沌运动,混沌运动区域有所增大.随着β的进一步增大,即β在[0.567,0.8]范围内时,系统响应主要为周期运动,出现周期6运动、周期2运动.与图6a相比,混沌运动区域明显减小,小窗口的周期运动减少,周期运动区域增大.不同的支撑刚度对系统动力学固有特性有明显影响.

4 结 论

1) 系统在以脉动频率ω为控制参数下,表现出周期运动、拟周期运动、混沌运动状态.观察到系统由混沌运动通往周期运动的倒分岔路径.选取一定支撑刚度系数情况下,混沌运动提前,拟周期运动区域增大,系统运动的交换频率增强.支撑刚度对系统响应影响显著.

2) 随着脉动幅值μ的增大,系统表现出跳跃间断现象、周期运动、拟周期运动和混沌运动频繁交替,系统路径以倍周期分岔的形式由周期运动过渡到混沌运动.此外,在选取一定支撑刚度系数情况下,系统的跳跃间断现象提前,支撑刚度在一定程度上引起系统固有特性的改变.

3) 随着质量比β的增大,系统出现周期性运动、拟周期运动和混沌运动状态.通过改变支撑刚度系数,系统混沌运动强度减弱,混沌运动区域明显减小,不同的支撑刚度对系统动力学固有特性产生明显影响.