考虑成批供料的大规模下料问题
郝信烨 刘懋圻 张灿荣 郑力








摘 要:本文基于某家具厂实际生产场景,在大规模下料问题中考虑了成批供料等现实生产因素。我们建立了Kantorovich模型,其对应的算例具有规模大、解空间对称等特点,难以直接求解。为了解决计算困难,基于Dantzig-Wolfe框架将其分解,并通过列生成求解线性松弛主问题得到较紧的下界。通过对子问题的结构分析,将其分解为可独立求解的二级子问题。基于归并且还原设计了三种子问题求解方式,有效缩减了子问题求解规模,并克服了解空间对称性,进而加速列生成迭代。基于工厂实际数据进行数值实验,结果表明:本列生成启发式算法优于商用求解器CPLEX,其在较短计算时间内得到高质量的解。相比于工厂现行算法,本算法降低10.43%的下料浪费。
关键词:板材下料;成批供料;大规模混合整数规划;列生成;归并且还原
中图分类号:TB114.1 文献标识码:A 文章编号:2097-0145(2022)01-0009-08 doi:10.11847/fj.41.1.9
Abstract:This paper stems from a real production research. It studies a large-scale cutting stock problem considering batch feed and some other constraints based on the real production. We establish a Kantorovich model, the instances corresponding to which are hard to solve due to the large scale and symmetry in the solution space. To tackle the computational difficulty, we decompose it based on the Dantzig-Wolfe framework, and solve the linearly-relaxed master problem by column generation in order to generate tight lower bounds. Based on the analysis of the structure, we decompose the sub-problems into second-level sub-problems which can be solved independently. Based on the idea of merge and recover, we develop three methods to solve the sub-problems, which reduce the scale of sub-problems and overcome the symmetry in the solution space, leading to accelerating the column generation process. We conduct computational experiments based on the real data from the factory. The experimental results indicate that, our approach outperforms CPLEX, a commercial solver. It can generate high-quality solutions in short computation time. Compared with the algorithm presently used in the factory, our approach reduces the cutting waste by 10.43%.
Key words:cutting stock; batch feed; large-scale mixed integer programming; column generation; merge and recover
1 引言
下料问题(Cutting Stock Problem,CSP)是众多行业中(如造纸业[1]、造船业[2])面对的一个重要问题,其以最小化成本为目标,通过对库存板材的切割,来满足不同尺寸类型的需求[3~5]。合理的下料方案会为实际生产减少浪费,带来经济效益。基于同某家具厂合作的实际生产项目,本文对该厂CSP进行研究。该厂拼合板产品生产过程如下,盛有不同規格板材的托盘被挑选并从仓库中运到线上,工人将刀具预设为若干种标准宽度,并在板材宽度方向上进行水平切割(顺冲工序),产生短条;之后,在垂直方向上切去影响美观的木料疤痕(横截工序),产生横截小块,并将横截小块指接成长条;最终,用从长条上切下的拼合块进行产品拼合。在此过程中,需要对如下问题进行决策,包括,如何挑选托盘来权衡运输成本和板材多样性,如何水平切割板材,如何选择宽度来拼合最终产品,从而降低板材浪费率。当前,工人们按照经验进行决策,材料浪费较为严重。
基于工厂实际生产情景,与经典CSP相比,我们额外考虑了成批供料等生产约束。据我们所知,本文是首个将托盘成批供料纳入CSP的研究。另外,本问题也有算例规模极大的特点,如算例“曲柳_27mm”具有272730个决策变量。据统计,现有的大多数文献中,模型的变量均远小于本文,如Song等[6]的模型中有32580个决策变量。由于CSP本身为NP-hard[7],且本问题具有额外的复杂特征,以及算例具有极大规模,因此,亟需开发高效、高质量的启发式算法,在实际生产中,求解时间受限的情况下使用。我们首先建立了Kantorovich模型(Kantorovich Model, KM)来精准表达原问题,但其算例规模大,且具有解空间对称等缺点,因此,空间复杂度较大,且用求解器难以直接求解。为了实现对本问题的高效求解,我们基于Dantzig-Wolfe 框架对KM按托盘分解,得到1个主问题(Master Problem, MP)与若干子问题,并通过基于列生成(Column Generation, CG)的启发式算法(Column Generation-based Heuristic, CGH)生成KM上界。为了加速CG 迭代,通过对模型结构的分析,我们发现子问题托盘与板材之间可分支求解的特点,进而可以将子问题分解为可独立求解的二级子问题,即,每个板材对应的下料模型,简称板材模型(Board Model,BM)。另外,相同规格的板材BM模型相同。基于此特性,我们设计了3种子问题求解方式:基于托盘的归并且还原,基于板材池的归并且还原,基于分解板材池的归并且还原。这些求解方式有效地缩减了子问题整体求解规模,并克服了解空间对称性的困难。我们从该工厂的生产管理系统中导出实际数据并进行测试,结果表明,我们的算法优于商用求解器CPLEX12.8.0,可以在较短时间内得到高质量的解。相比于工厂现行下料算法,我们的算法能够为工厂降低10.43% 的下料浪费,从而极大地节约生产成本。
2 文献综述
作为组合优化的经典NP-hard问题[7],CSP始终是学者们关注的焦点。CSP在现有研究中有两种主要的建模方式。第一种是Kantorovich[8]最先对CSP进行定义并建立的带有指派类型决策变量的数学模型(后续称之为Kantorovich模型)。Kantorovich模型直接决策并清楚指示了每块板材应该生产的产品。基于本模型,学者们开展了一系列研究。Abuabara 和Morabito[9]研究了航空材料工厂的一维CSP,他们建立了Kantorovich模型并直接通过CPLEX求解。Lee等[10]针对产品形状可变的二维的CSP建立Kantorovich模型,并设计了基于背包问题模型的启发式算法来求解。管卫利等[11]基于Kantorovich 模型,对单规格和多规格线材切割进行数值实验。在Kantorovich模型中,当很多板材之间具有相同规格时,解空间会存在很严重的对称性,即解不同但目标函数值相同。此缺点对于基于“分支—定界”框架来求解整数规划的求解器(如,CPLEX)来说,会引发长时间无效的分支,当问题规模过大,会难以求解。另外,虽然Kantorovich模型线性松弛产生的下界在需求宽度种类较少的情况下质量较高,但其空间复杂度较大,建立模型需要占用较多内存和相对较长时间。
下料问题的第二种模型是Gilmore和Gomory[3,4]提出的基于下料方案的模型(后续称之为Gilmore-Gomory模型),此模型克服了Kantorovich模型中对称性的缺点,同时,其线性松弛模型提供比线性松弛的KM(Linearly-relaxed KM, LKM)更紧的下界。与Kantorovich模型不同,Gilmore-Gomory模型并没有直接指出每块板材产出的产品,而是基于每块板材可以切割得到的产品的组合(即下料方案)进行选择。但在本模型中,下料方案随着产品规模而指数级增长,因此模型中会有很多列。为了解决此问题,Gilmore和Gomory[3,4]提出了CG算法,来动态地生成列,进而对线性松弛的Gilmore-Gomory模型精确求解。之后,可基于此线性松弛解对原问题进行启发式或精确求解。Belov和Scheithauer[12]研究了一维、单规格板材的CSP,他们建立了Gilmore-Gomory模型,并通过分支—定价框架进行求解。Cui 和Zhao[13]研究了二维的单规格CSP。在该研究中,下料得到的产品可以旋转,此特征使得问题更加复杂。Furini等[14]研究了多规格板材、两阶段一刀切的二维CSP,并设计了基于CG的启发式方法来求解。Wuttke和Heese[15],Wang等[16]研究的CSP中,考虑了板材生产准备成本。下料问题的其他模型,如De Carvalho模型[17]和Dyckhoff模型[18],由于同本文的模型关联较少,因此不做讨论。
本研究中,我们将板材成批供料等约束引入CSP,这在现有研究中属于首次。另外,我们基于含有超过20万变量的实际算例进行数值实验,据我们所知,当前研究中尚未有如此大规模实际算例的测试。我们首先建立KM来对原问题进行描述。为了高效求解原问题,我们通过Dantzig-Wolfe框架将其分解为一个主问题(Master Problem, MP,即,Gilmore-Gomory模型)和若干子问题,并用CG 求解线性松弛的主问题(Linearly-relaxed Master Problem, LMP)来得到较紧的下界。通过对子问题性质分析,我们设计了子问题不同的求解方式,从而加速CG迭代过程。最后,我们通过启发式挑选列,生成原问题的高质量上界。
3 问题描述与数学模型
本部分我们对实际生产情景进行描述,并建立KM。
3.1 问题描述
我们研究的是在某工厂实际生产中的考虑成批供料和材料等级的大规模CSP。本工厂主要产品为拼合板家具,其生产流程如图1所示,具体描述如下。
步驟1 选择托盘并运输。工人选择盛放不同批次板材的托盘,并运送至下料车间。
步骤2 选择板材。工人选择将要下料的板材。
步骤3 顺冲。工人把选择的板材放在下料机上,按照设定好的若干种标准切割宽度(52mm, 62mm, 81mm和89mm)进行水平切割,产生短条。
步骤4 横截。工人把短条放到另一种下料机上进行横截,垂直切掉短条上的疤痕,产生横截小块。
步骤5 指接。工人将横截小块指接成长条。
步骤6 拼合,去余料。工人从长条上切下与产品长度相同的拼合小块,并将拼合小块在宽度方向上进行拼合,直至达到产品宽度。最终,宽度方向上多余的部分被切掉,得到最终的拼合板产品。
除以上描述之外,我们研究的问题有如下特征:
(a)大规模:厂方的生产管理系统中导出的数据显示,托盘和板材的数量非常多,导致算例规模较大。如,算例“曲柳_27mm”含有150个托盘和12980块板材,其Kantorovich模型具有272730个决策变量,模型规模远超大多数现有研究。
(b)成批供料:不同托盘盛放不同批次板材,不同批次板材规格有差异。选择某个托盘后,托盘上的一批各种规格(长、宽)的板材被运送到线上进行切割。这需要权衡托盘运输成本与板材的多样性。
(c)材料等级:为了实现产品差异化,以应对消费者不同的偏好,本工厂将最终生产的拼合板产品分为不同等级。每个板材、短条都标有质量类型(即A,B,C,D),横截小块、长条、产品都有质量等级(如1,2,3,4,数字越小,等级越高)。关系如下:板材经过横截工序产生的短条与板材的质量类型相同;在步骤4横截中,不同质量类型的短条会按不同比例(即出料率)产生不同质量等级的横截小块,如表1 所示;某类型的横截小块只能指接入宽度等于它且等级不高于它的长条中;长条切得的拼合小块的等级与其相同;拼合小块的等级必须不低于它拼合而成的产品。需要说明的是,表1 中,出料率之和均小于1,因为板材必有疤痕带来的物料损耗。
目前,工厂要求按照“最小余料”原则选择产品拼合宽度,即对每种产品,选择最终去掉余料最少的宽度的小块进行拼合,且小块的等级要与产品相同。基于此规则,我们首先将产品需求转化为相应宽度和等级的长条,称为“延米数”。以此为生产需求,关注下料方案的设计。另外,我们假设除了必要的去余料与去疤痕过程,其他生产过程没有物料损失。
3.2 数学模型
本部分我们建立KM。首先,我们给出符号表示。在本文的数学模型中,除集合外,所有输入变量小写,决策变量大写。
集合与索引:P为托盘集合,用p索引。B为板材集合,用b索引。Ωp 为托盘p中的板材集合。N为标准切割宽度集合,用n索引。Q为板材质量类型集合,用q索引。G为质量等级,用g索引。
目标函数(1)最小化总成本,包括托盘运输成本与板材使用成本。约束(2)保证只有选择了某托盘,其中的板材才能被选择。约束(3)为板材宽度约束。约束(4)保证对于所有板材,其每种宽度的短条产生的延米数不能超过短条对应的总长度。约束(5)为出料面积约束,我们假设理想情况,即出料时每个等级都可以达到其最大出料面积。约束(6)为考虑向下兼容的需求满足约束。约束(7)和(8)说明决策变量的性质。
4 求解方法设计
本节包括如下内容:首先,我们按照Dantzig-Wolfe框架,将KM按托盘分解为MP和子问题。之后,介绍生成初始列与生成原问题上界的启发式方法。最后,基于子问题的模型结构进行性质分析,并介绍三种子问题求解方法。
4.1 Dantzig-Wolfe分解模型
本部分我们按照Dantzig-Wolfe框架,将KM按照托盘分解为1个MP与|P|个子问题模型。本模型具有角块结构,即子问题模型之间无耦合关系,因此,子问题可以独立求解。首先,引入如下符號表示。
目标函数(9)最小化所有被选择方案中的总成本,包括托盘运输成本与板材使用成本。约束(10)对应于约束(6),即需求满足约束。约束(11)说明每个子问题必须选择一个可行方案。约束(12)为决策变量性质说明。除此之外,我们引入2组对偶变量:α和β,分别对应于LRMP中的约束(10)和约束(11),用来构建子问题的目标函数。
(2)子问题模型
目标函数(13)包括托盘运输成本、板材使用成本,以及与对偶变量有关的目标。约束(14)~(17)对应KM中的(2)~(5)。
4.2 初始列和上界构建方法
为了使CG开始迭代,我们设计如下初始列构建方法。基本原则是,对于所有n∈N,g∈G,顺序地不断搜索未满足的需求dng。 若有未满足需求,则顺序抽取托盘以及托盘中的板材。若板材剩余宽度不小于需求宽度,那么宽度方向水平切割一刀(顺冲),得到的短条按照出料率产出横截块,横截块按照等级向下满足需求。
同时,我们设计基于LRMP的一种上界构造方法。本方法的基本原则是,当LRMP求解完毕,针对每个托盘p∈P,我们将mp∈Θp对应的解值作为概率,来随机抽取该托盘p的一个下料方案,并用该方案来满足需求延米数。当所有托盘抽取的方案无法满足需求时,我们从第一个托盘顺序筛查未切割或剩余足够宽的板材,并按照构造初始列中提到的方法进行切割和需求满足。
初始列和上界构造详细流程如图2所示。图2 初始列(a)和上界(b)构造流程
4.3 子问题性质分析与算法设计
本部分基于子问题的模型结构,首先对子问题性质进行分析。基于其托盘选择—板材选择决策可分支特性,及BM模型特点,我们设计了三种精确求解方法,既缩减了问题规模,又消除了解空间的对称性。
(1)子问题性质分析
由于板材对应BM可独立求解,因此,我们分别求得每个板材对应的BM目标值即可。更进一步地,对于相同规格(即长、宽、质量类型均相同)的板材,由于其BM相同,因此,我们只需要求解不同规格板材对应的BM,再将解通过板材-托盘进行数量匹配,即可还原成各个子问题的解。根据此思路,我们进行子问题如下求解方式的设计。
(2)子问题求解方式
本部分介绍三种子问题求解方式,如(a)~(c),根本原则是提取不同规格(即长、宽、质量类型至少存在一种不同)的板材模型进行求解,并通过板材-托盘匹配关系还原出子问题的解。子问题求解方式的图形化表达,如图2所示,其中T代表板材规格。具体说明如下。
(a)基于托盘的归并且还原
本算法的核心是,在每个托盘中,提取出不同规格的板材,并将这些不同的板材打包成一个集合,得到一个规模更小的缩减的子问题。通过CPLEX求解此缩减的问题,再通过板材-托盘数量关系线性相加,从而还原出子问题的解。缩减的问题不仅规模更小,而且不存在解空间对称性,因此,求解速度更快。
(b)基于板材池的归并且还原
算法(a)中,虽然对于每个缩减的子问题不存在解空间对称性,但是由于不同托盘中存在相同规格的板材,因此,从全局来说,存在对于相同BM的重复求解,这将会带来时间的浪费。因此,我们考虑直接将相同规格的板材打包,命名为“板材池”。对板材池对应的模型进行求解,通过b∈Ωp的匹配关系,以及板材在托盘中的数量关系来进行子问题解的还原,即将板材池中与托盘匹配的BM目标值线性相加。
(c)基于分解板材池的归并且还原
算法(b)中,显然,若板材池规模过大,求解效率会降低。因此,我们考虑将板材池进行分解求解,分解规模在100~500之间随机产生。由于相同规格的板材对应的BM相同,因此本算法得到的各BM的解仍是各个BM的最优解。基于还原操作,可以得到各个子问题的最优解。
5 数值实验
本部分包括如下内容。首先,我们展示输入数据的规模。然后,通过CPLEX求解KM的结果说明,在算例大规模情况下,直接求解难度较大和设计启发式算法的必要性。随后,我们测试了CGH的性能,如计算效率与可行解的质量。最后,我们评价了CGH在实际指标(如浪费率)上的表现。所有的模型和算法均基于Java编写,数值实验均在Windows服务器上进行,处理器为Xeon E7-8850 2.00GHz,运行内存为512G,CPLEX版本为12.8.0。
5.1 原始输入数据规模
本部分展示从该工厂生产管理系统中导出算例的数据规模,总结如表3所示。算例名称格式为“原材料_厚度”,如“曲柳_10mm”指原材料为10mm厚的曲柳。由表中结果可见:算例规模均较大,变量数量均超过20万,远超当前其他研究中的算例规模;通过按照板材的长、宽、质量类型进行归并,发现板材种类远小于板材数量,如“曲柳_27mm”算例中有12980个板材,归并数据显示其规格只有1595 种。因此可得两方面结论,其一,若用CPLEX直接求解KM,其解空间严重的对称性会严重影响“分支—定界”的效率,从而导致CPLEX难以求解。其二,说明了我们基于按板材规格缩减的方法求解子问题有意义。我们定义“供给/需求面积比”,即每个算例中,托盘中所有板材的总面积,除以计划生产的产品总面积。结果中,较大的供需比说明提供板材过多,一定程度上会导致求解困难,但为了在全局上获得更高质量的解,我们选择根据原始输入数据直接进行计算。
5.2 CPLEX性能测试
我们调用CPLEX12.8.0对以上算例进行求解。按照工厂对计算时间以及对解的质量的要求,我们设定CPLEX满足如下条件之一即停止。
(a)达到最大计算时间7200s。
(b)算例上下界界限收敛至1.00%或以下。
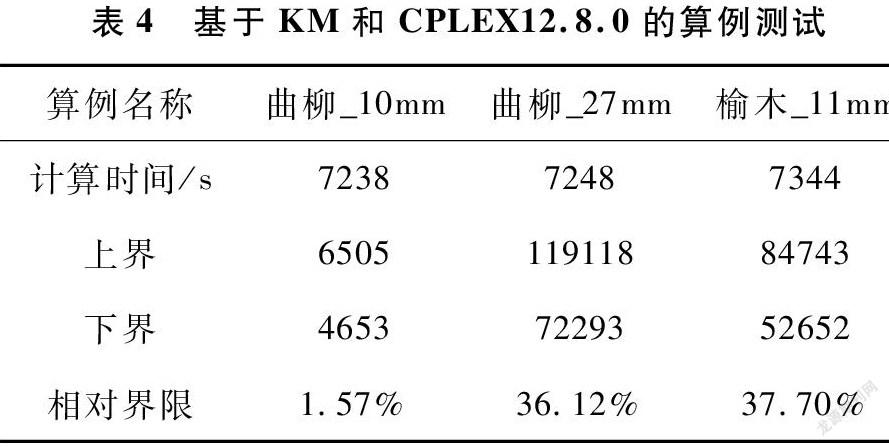
实验结果如表4所示。
由结果可见,算例本身规模较大,且存在严重的解空间对称性,导致CPLEX直接求解KM表现较差。因此,亟需开发能够快速产生较优解的启发式算法,便于工程应用。
5.3 CGH性能测试
本部分测试CGH的算法性能。我们将三种子问题求解方式对应的CGH算法分别表示为CGH1、CGH2及CGH3,并分别测试如上三个算例。在列生成迭代时,每5次迭代调用一次上界启发式算法。我们将CGH的停止條件设为如下,当其中任意一个满足时,停止迭代。
(a)达到最大计算时间:CGH每次迭代的当前时刻达到或超过7200s。
(b)CGH产生的上界与CG下界的相对界限收敛至1.00%或以下:计算方式为GapCGH-CG=UBCGH-LBCGUBCGH×100%,其中UBCGH表示CGH产生的原问题上界,LBCG表示CG产生的原问题下界。
(c)无有效可添加列:当所有子问题的目标值均大于-10-5时,视为无有效可添加列。
通过与厂方沟通,我们总结出他们主要关注如下评价指标:
(a)计算时间:目前,厂方要求计算时间控制在7200s之内,计算效率需要尽可能高。
(b)总成本:即目标函数值或可行解。首先,我们用GapCGH-CG评价可行解的质量。另外,我们也关注CGH产生的上界与KM得到的上界(UBKM)的相对界限,计算方式为
以及CG产生的下界与LKM得到的下界(LBLKM)的相对界限,计算方式为
(c)下料浪费率:在“横截”步骤中,剩余的短条宽度小于最低标准宽度52mm。由于机器工艺的限制,这些短条无法继续被切割,因此,是一种浪费,计算方式为
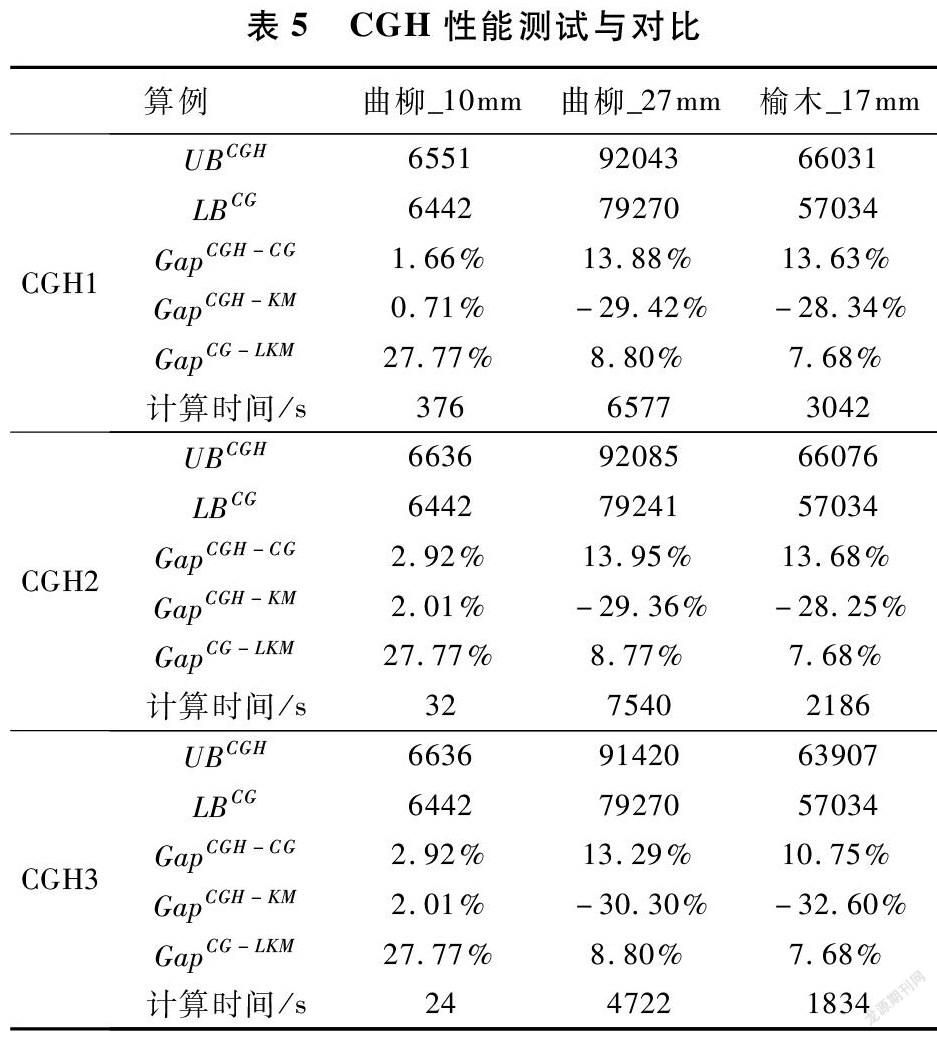
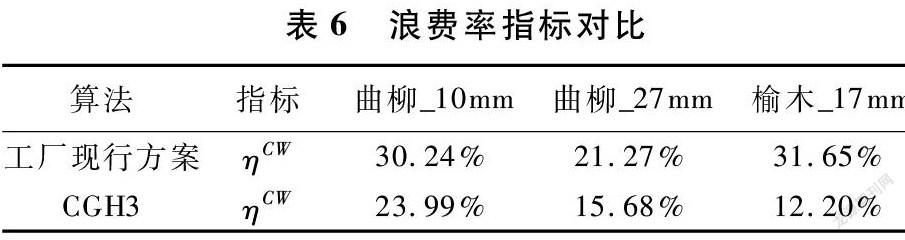
此外,我们根据工厂现行下料方式,即按照“先到先服务”原则,不断抽取托盘及板材,并按照尚未满足的最窄的需求进行下料。我们计算了工厂关于如上算例的实际的浪费率指标。统计结果如表5和表6,我们基于指标(a)~(c),有如下两点总结。
(1)解的质量与计算效率:总的来说,三种子问题求解方法均可以产生高质量解,且CGH3效率最高。可行解质量方面,对于算例“曲柳_10mm”,CGH在较短时间内产生的可行解质量与CPLEX7200s之内产生的可行解质量基本相同,且用时最短在30s之内。对于另外2个算例,CGH可行解质量较CPLEX提高30.00%左右,这显示了CGH求解大规模算例时的有效性。下界方面,CG均可提供比LKM更紧的上界。收敛性方面,CGH可行解距离CG下界的相对界限均在15.00%之内,这在大规模算例用CPLEX难以求解时,提供了较好的可行解质量评估标准。效率方面,CGH3效率明显高于其他两种方法。CGH2 中,由于其板材池对应的数学模型规模过大,导致CPLEX求解耗时过多,如算例“曲柳_27mm”,此结果与我们对三种缩减方法的分析是一致的。
(2)下料浪费率:基于工厂当前下料算法,平均下料浪费率为27.72%。基于CGH3的求解结果,平均下料浪费率为17.29%。可见,我们开发的CGH 降低平均下料浪费率10.43%。 另外,我们发现了“曲柳_10mm”浪费率高的原因:本算例中,板材宽度均为90mm,只能顺冲出一条短条,当短条宽度与板材宽度相差较大时,会产生相对较多浪费,这也提示工厂在购买板材时可多考虑较宽板材。
综上,我们基于子问题模型结构性质开发的CGH3优于CPLEX,它可以在较短时间内得到更高质量的解。CGH3不仅解决了原模型中解的对称性缺点,同时很大程度上缩减了算例规模,使得大规模算例可以快速求解。与工厂现行下料方案对比,CGH3降低平均下料浪费率10.43%,带来成本节约。
6 结论与展望
本文基于同某家具厂的实际生产合作项目,在CSP中考虑了成批上料等现实生产因素。我们首先基于生产情景建立数学模型KM。为了克服大规模算例的求解困难,我们基于Dantzig-Wolfe 框架,将KM 分解为一个MP和若干子问题,并基于CG对LMP进行求解,进而用基于启发式挑选列的CGH方法,生成原问题上界。为了加速CG迭代,通过对子问题结构的分析,我们发现子问题的可分支特性,进而将子问题分解为可独立求解的二级子问题BM。基于此特征,我们开发了三种高效的子问题求解方式:基于托盘的缩减且还原,基于板材池的缩减且还原,基于分解板材池的缩减且还原。基于从工厂生产管理系统中导出的实际算例,我们进行数值实验,结果表明,当由于问题规模过大以及解空间对称性严重而导致CPLEX 求解性能极差时,CGH3 可以高效求解此大规模问题,在较短时间内产生高质量的解。如对于三个算例,CGH3产生的可行解质量与CPLEX可行解相当(如稍差2.01%)或更优(如质量提高30.30%、32.60%),CGH和CG的上下界平均相对界限为8.99%,且运行时间远低于CPLEX。 在实际的浪费率指标上,CGH3也有较好表现。通过与工厂现行下料方案相比,CGH3 降低平均下料浪费率10.43%。
我们的研究亦有可拓展之处。(1)尝试其他分解思路,如将KM直接按照板材分解且按照板材挑选下料方案并构建上界。(2)板材池分割求解时,较宽的板材按照较小规模分解,而较窄板材由于背包约束的解空间较小,单个BM求解较快,可以按照较大规模分解。(3)联立考虑下料和拼合工序,理论上将产生不会比当前更差的最优解。
参 考 文 献:
[1] Kallrath J, Rebennack S, Kallrath J, et al.. Solving real-world cutting stock-problems in the paper industry: mathematical approaches, experience and challenges[J]. European Journal of Operational Research, 2014, 238(1): 374-389.
[2] 吴电建,阎春平,李俊,等.而向可加工性的矩形件优化下料方法[J].计算机集成制造系统,2018,24(6):1374-1382.
[3] Gilmore P C, Gomory R E. A linear programming approach to the cutting-stock problem[J]. Operations Research, 1961, 9(6): 849-859.
[4] Gilmore P C, Gomory R E. A linear programming approach to the cutting stock problem-Part II[J]. Operations Research, 1963, 11(6): 863-888.
[5] Melega G M, de Araujo S A, Jans R. Classification and literature review of integrated lot-sizing and cutting stock problems[J]. European Journal of Operational Research, 2018, 271(1): 1-19.
[6] Song G P, Kowalczyk D, Leus R. The robust machine availability problem-bin packing under uncertainty[J]. IISE Transactions, 2018, 50(11): 997-1012.
[7] Bischoff E E, Wascher G. Cutting and packing[J]. European Journal of Operational Research, 1995, 84(3): 503-505.
[8] Kantorovich L V. Mathematical methods of organizing and planning production[J]. Management Science, 1960, 6(4): 366-422.
[9] Abuabara A, Morabito R. Cutting optimization of structural tubes to build agricultural light aircrafts[J]. Annals of Operations Research, 2009, 169(1): 149.
[10] Lee J, Kim B, Johnson A L. A two-dimensional bin packing problem with size changeable items for the production of wind turbine flanges in the open die forging industry[J]. IIE Transactions, 2013, 45(12): 1332-1344.
[11] 管衛利,龚击,薛焕堂.一维下料问题的一种混合启发式算法[J].机械设计与制造,2018,(8):237-239.
[12] Belov G, Scheithauer G. A branch-and-cut-and-price algorithm for one-dimensional stock cutting and two-dimensional two-stage cutting[J]. European Journal of Operational Research, 2006, 171(1): 85-106.
[13] Cui Y, Zhao Z. Heuristic for the rectangular two-dimensional single stock size cutting stock problem with two-staged patterns[J]. European Journal of Operational Research, 2013, 231(2): 288-298.
[14] Furini F, Malaguti E, Durán R M, et al.. A column generation heuristic for the two-dimensional two-staged guillotine cutting stock problem with multiple stock size[J]. European Journal of Operational Research, 2012, 218(1): 251-260.
[15] Wuttke D A, Heese H S. Two-dimensional cutting stock problem with sequence dependent setup times[J]. European Journal of Operational Research, 2018, 265(1): 303-315.
[16] Wang D, Xiao F, Zhou L, et al.. Two-dimensional skiving and cutting stock problem with setup cost based on column-and-row generation[J]. European Journal of Operational Research, 2020, 286(2): 547-563.
[17] De Carvalho J M V. Exact solution of bin-packing problems using column generation and branch-and-bound[J]. Annals of Operations Research, 1999, 86: 629-659.
[18] Dyckhoff H. A new linear programming approach to the cutting stock problem[J]. Operations Research, 1981, 29(6): 1092-1104.
3631500338258

