哥尼斯堡七桥问题与图论

蔡思明

1736年29岁的欧拉向圣彼得堡科学院递交了《哥尼斯堡的七座桥》的论文，在解答问题的同时，开创了数学的一个新的分支——图论.

一、哥尼斯堡七桥问题

哥尼斯堡在俄罗斯境内，曾是东普鲁士的首府，现称为加里宁格勒.哥尼斯堡是一座历史名城，这里诞生和培养过许多伟大人物.哥尼斯堡城中有一条布勒格尔河，横贯城中，如图1所示.布勒格尔河有两条支流，一条称为新河，另一条叫做旧河，在城中心汇合成一条主流，在合流的地方有座河心岛，这是城中繁华的商业中心.布勒格尔河将全城分成为四个地区：岛区、北区、东区和南区.人们在布勒格尔河上架了七座桥，其中五座将河岛与河岸连接起来，另有两座架在两支流上.这一别致的桥群，吸引了众多的哥尼斯堡居民和游人来此河边散步或去岛上买东西.

1735年，有几名大学生写信给当时正在俄国彼得堡科学院任职的天才数学家欧拉，请他帮助解决这个问题.欧拉并未轻视这个生活小问题，他似乎看到其中隐藏着某种新的数学方法.经过一年的研究，29岁的欧拉圆满地解决了这一问题，并于1736年向彼得堡科学院递交了一篇题为《哥尼斯堡的七座桥》的论文.

二、欧拉的解法

欧拉的答案是：想一次不重复地走过这七座桥是不可能的.那么欧拉是如何解决这个问题的呢？他用点A、B、C、D表示哥尼斯堡城的四个地区C（岛区）、B（北区）、D（东区）、A（南区）;七座桥看成这四个点的连线，用1、2、3、4、5、6、7七个数字表示，如图3所示.这样“七桥问题”就转化为“一笔画”问题：否能一笔不重复地画出过此七点的图形.

假设可以画出来，则图形中必有一个起点和一个终点，如果这两个点不重合，则与起点或终点相交的线都必须是奇数条（称奇点），如果起点与终点重合，则与之相交的线必是偶数条（称偶点），而除了起点与终点外的点也必是“偶点”.由对称性可知由B或C为起点得到的结果是一样的，若假设以A为起点和终点，则必有一离开线和对应的进入线，若我们定义进入A的线的条数为人度，离开线的条数为出度，与A有关的线的条数为4的度，则4的出度和入度是相等的，即4的度应该为偶数.即要使得从4出发问题有解，则4的度数应该为偶数，而实际上4的度数是5，为奇数，于是可知从4出发，问题是无解的.同时若从B或D出发，由于B、D的度数分别是3、3，都是奇数，即以之为起点，问题都是无解的.

由上述分析可知，如果一个图形可以一笔画出来，须满足如下两个条件：

（1）图形必须是连通的，即图中的任一点通过一些线一定能到达其他任意一点.

（2）图中的“奇点”数只能是0或2.

我们也可依此来检验图形是否可一笔画出.回头来看看“七桥问题”，图3中的4个点全都是“奇点”，可知该图不能“一笔画出”，也就是不可能不重复地通过七座桥.欧拉发表的这一结果，震惊了当时的数学界，人们无不赞叹这位数学天才的能力！

三、对“七桥问题”的引申推广

1.过了许多年，河上又架起了第八座桥——铁路桥，如图4所示.这座桥的建成，使人们又想起了那个有趣的“七桥问题”.那么，可一次不重复走过八座桥吗？从图5的简化模型可知“奇点”只有两个（D点和C点），所以可以一次不重复地走过八座桥.

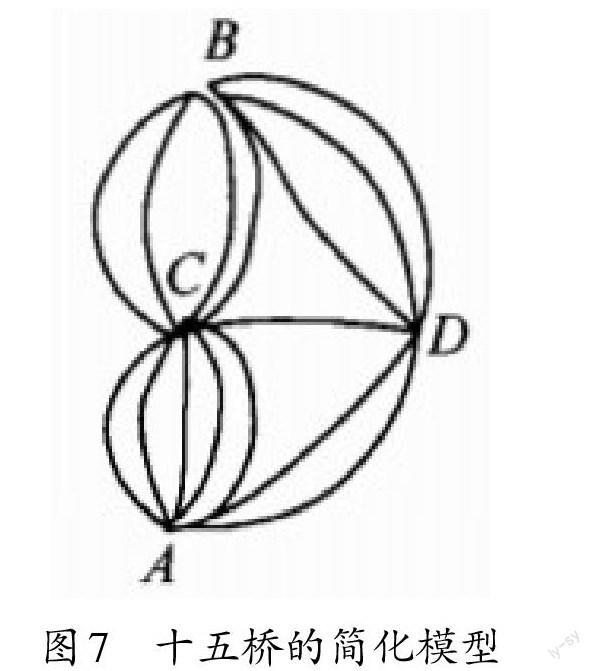
2.若有一条河，河中心有两个河心岛，有十五座桥把这两个岛和两岸连接起来，如图6所示，问能否不重复地通过这十五座桥？按欧拉的方法，把图抽象成如图7所示的简化模型，由于图中只有A、B两个“奇点”，故该图可以一笔（不重复）画成，即可以不重复地通过15座桥.

四、图论的形成

欧拉在解决“哥尼斯堡七桥问题”的过程中，开创了一个新的数学分支——图论.他所使用的方法是图论中常用的方法.欧拉的这个结论标志着图论的诞生，即研究由线连接的点组成的网络.用现在图论的术语来说，哥尼斯堡七桥问题属于一笔画问题：如何判断这个图是否是一个能够遍历完所有的边而没有重复的图.如果存在这样的方法，该图则称为欧拉图.这时遍历的路径称作欧拉路径（一个环或者一条链），如果路径闭合（一个圈），则称为欧拉回路.

图论中的欧拉定理（一笔画定理）要分有向图（边有特定方向的图）与无向图（边没有特定方向的图）两种情况进行讨论.

1.无向图的情况

定理：连通无向图G有欧拉路径的充要条件为：G中奇度顶点（即与其相连的边数目为奇数的顶点）有0个或者2个.

证明：必要性.

如果图能够被一笔画成，那么对每个顶点，考虑路径中“进入”它的边数与“离开”它的边数（注意前提是无向图，所以我们不能称其为“人边”和“出边”）.很显然这两个值要么相同（说明该顶点度数为偶），要么相差1（说明该顶点度数为奇）.

也就是说，如果欧拉路径不是回路，奇度顶点就有2个，即路径的起点和终点;如果是欧拉回路，起点与终点重合，则不存在奇度顶点.必要性得证.

证明：充分性.

如果图中没有奇度顶点，那么在G中随机取一个顶点v₀出发，尝试构造一条回路c₀.如果c₀就是原路，則结束;如果不是，那么由于图是连通的，c₀和图的剩余部分必然存在某公共顶点v₁，从v₂出发重复尝试构造回路，最终可将整张图分割为多个回路.由于两条相连的回路可以视为一条回路，所以该图必存在欧拉回路.

如果图中有2个奇度顶点u和v，那么若是加一条边将u和v连接起来的话，就得到一个没有奇度顶点的连通图，由上文可知该图必存在欧拉回路，去掉这条新加的边，就是一条以u和v为起终点的欧拉路径.充分性得证.

可知，哥尼斯堡七桥问题中的图有4个奇度顶点（1个度数为5，3个度数为3），所以不存在欧拉路径.

2.有向图的情况

定理：底图连通的有向图G有欧拉路径的充要条件为：G的所有顶点入度和出度都相等;或者只有两个顶点的入度和出度不相等，且其中一个顶点的出度与入度之差为1，另一个顶点的入度与出度之差为1.

显然，可以通过与无向图情况相似的思路来证明，过程略.

当时的数学界起初并未对欧拉解决七桥问题的意义有足够的认识，甚至有些人仅仅当其为一个数学游戏.图论这一数学分支诞生后并未得到很好的发展，直到200年后的1936年，匈牙利数学家科尼希出版了《有限图与无限图理论》，此为图论的第一部专著，其总结了进200年来有关图论的成果，这是图论发展的第一座里程碑.此后，图论进入发展与突破的阶段，又经过了半个多世纪的发展，现已成为数学科学的一个独立的重要分支.

图论原是组合数学中的一个重要课题.我们用点表示事物，用连接点的边表示事物间的联系，便可得到图论中的图.图论为研究任何一类离散事物的关系结构提供了一种框架.图论中的理论已应用于经济学、心理学、社会学、遗传学、运筹学、逻辑学、语言学计算机科学等诸多领域.

由于现代科学尤其是大型计算机的迅猛发展，使得图论大有用武之地，无论是数学、物理、化学、地理、生物等基础科学，还是信息、交通、战争、经济乃至社会科学的众多问题，都可以运用图论方法予以解决.当然，图论也是计算机科学的基础学科之一.

值得一提的是，欧拉对七桥问题的研究，后演变成多面体理论，得到了著名的欧拉公式V+F=E+2，欧拉公式是拓扑学的第一个定理.

哥尼斯堡的七座桥如今只剩下三座，一条新的跨河大桥已经建成，它完全跨过河心岛——内福夫岛，导游们仍向游客讲述哥尼斯堡桥的故事，有的导游甚至仍称“七桥问题”没有被解决，留给游客以遐想.虽然七座哥尼斯堡桥成了历史，但是“七桥问题”留下的“遗产”不像这些桥那样容易破坏，欧拉卓越的解答方式被永载史册.