立足基础求创新　关注本质重发展

钱小强　钱德春

【摘 要】数学压轴题的命制要立意先行，聚焦目标的指向性;源于教材，着眼问题的发展性;立足基础，注重试题的创新性;关注本质，追求试题的关联性;简约精致，彰显试题的人文性.

【关键词】命题立意;立足基础;关注本质;简约精致;注重发展

笔者有幸参加了所在地区2021年秋季学期期末八年级数学试卷的命制工作.试卷的压轴题从教材一道经典问题出发，通过精心设计、反复推敲、细心打磨，最终呈现的试题既考查学生的基础知识与基本技能，也考查学生的探究意识与创新能力.问题所蕴涵的“变与不变”“数形结合”等思想方法引领学生关注数学本质，寻求问题解决的一般规律与方法，有利于发展学生的数学思维能力.试题简约精炼，体现了对学生的人文关怀.本文基于试题命制与打磨过程的阐述，谈谈“立足基础求创新、关注本质重发展”的初中数学命题思考.1 真题及简答

如图1，在平面直角坐标系xOy中，点A，B的坐标分别为（-4，0）、（0，3），连接AB，点P是线段AB上的一个动点（与点A，B不重合），过点P作PC⊥x轴，垂足为C，将线段BC绕点B逆时针旋转至BD，使∠CBD=∠ABO.连接OD，设点P的横坐标为m.图1备用图

（1）求直线AB的函数表达式;

（2）当m为何值时，△BPC≌△BOD;

（3）在点P运动的过程中，

①在y轴上是否存在一点E，使得∠BED的大小始终不发生变化？若存在，请求出点E的坐标;若不存在，请说明理由;

②直接写出OD长度的取值范围.

本题取材于教材原题，以平面直角坐标系为载体，通过对图形运动中的变与不变规律的探究，考查了全等三角形、勾股定理、直角坐标系及一次函數等知识灵活运用能力、分析问题与解决问题能力，以及对“数形结合”“变中不变”等数学思想方法的感悟.简答如下：

（1）y=34x+3.

（2）当m=-125时，△BPC≌△BOD.

理由：当m=-125时，yP=65，所以AC=85，CP=65，由勾股定理得：AP=2，AB=5，所以BP=AB-AP=3，所以BO=BP，因为∠CBD=∠ABO，所以∠PBC=∠OBD，从而有△BPC≌△BOD.

（3）①存在.如图2，在y轴上取点E（0，-2），连接DE.易证△EBD≌△ABC，所以∠BED=∠BAC，由于∠BAC的大小不变，所以∠BED的大小也不变.

②因为点P运动的过程中，∠BED大小始终不变，所以点D在射线ED上运动.

当点P与点A重合时，点C与点A重合，点D与点E重合，此时D（0，-2），OD=2;图2 图3

当点P与点B重合时（如图3），点C与点O重合，此时点D运动至点D1处，过点D1作D1H⊥OB，易得△BAC≌△BED1，所以∠BD1E=∠BCA=90°，D1E=CA=4，求得D1H=125，从而BH=95，OH=65，进而OD1=655>2.

当OD⊥ED1时，OD的长度最小，因为BO=BD1，易证∠OD1H=∠OD1D，所以OD=OH=65.点D从点E运动至点D1的过程中，OD的长度先变小后变大，所以65≤OD<655.2 命题历程

2.1 命题立意

由于考查内容为苏科版八年级上册的全等三角形、轴对称图形、勾股定理、直角坐标系及一次函数，故将命题立意确定为：从教材经典问题出发，以平面直角坐标系为背景，考查相关基础知识、基本方法的灵活运用以及通过几何推理与代数运算解决问题的能力，体现“数形结合”与“变中不变”等数学思想方法.

2.2 问题原型

（苏科版八年级上册第67页“2.5等腰三角形的轴对称性”习题第10题）已知：如图4，△ABC和△CDE都是等边三角形，且点A，C，E在一条直线上.AD与BE相等吗？证明你的结论.

这是一道经典问题，由已知条件易得∠ACD=∠BCE，从而证得△ACD≌△BCE，得AD=BE.问题解决运用了等边三角形性质、全等三角形判定等知识与方法.从图形变换的角度看，全等的两个三角形可看作是绕点C旋转60°而得.

那么笔者思考：能否从该问题出发，通过改变图形结构、添加问题背景及设置附加条件，命制既考查相关章节的核心知识，又能渗透数学思想方法，还能反映数学本质的数学问题呢？

2.3 试题命制

明确了命题立意、找到了命题素材，接下来就是试题命制层面的工作.试题命制经历了“化静为动、数形结合，明晰主次、以动带动，适当铺垫、合理优化，删繁就简、简中求道”的不断取舍与整合、优化与完善的过程.

2.3.1 化静为动，数形结合

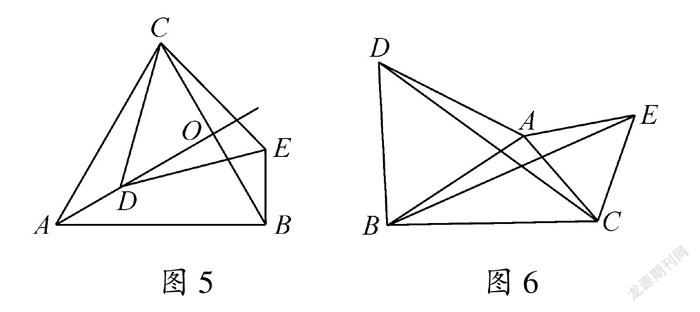
教材问题中的两个等边三角形的公共顶点C与另两个顶点A，E在同一直线上.当点A，C，E不在一条直线上时，如图5，根据“SAS”仍有△ACD≌△BCE，故AD=BE、∠CAD=∠CBE仍然成立.事实上，人教版八年级上册“第十三章轴对称”复习题第12题：“如图6，△ABD，△AEC都是等腰三角形.求证BE=DC.”正是研究的三点不共线情形.图5无论点D怎么变化，若∠CAD大小不变，∠CBE的大小也不变，若点D沿着射线AD运动时亦如此.基于这样的思考，将图形中的元素动起来，再寻求变化中的不变，便于利用直角坐标系与直角三角形线段关系代数化解决.要保证∠CAD大小不变，令AD⊥BC，将图形位置特殊化.于是，试题初稿出笼. 图7

一稿 如图7，在平面直角坐标系xOy中，△ABC和△CDE都是等边三角形，AC=4，点B，C在y轴上，点D为x轴上点A右侧的一个动点.

（1）试探索：在点D运动的过程中，∠CBE的大小发生变化吗？请说明理由;

（2）连接OE，求OE长度的最小值.

这里的问题（1）是问题（2）的铺垫，由前面的分析可知：无论点D如何运动，由于∠CBE=∠CAD，而∠CAD=30°保持不变，所以∠CBE也不变.事实上，由等边三角形ABC易得∠CAO=30°，故点E在y轴右侧且与射线BO所夹的角为30°的射线上运动.由“点到直线垂线段最短”知：在点E的运动过程中，点A，C，O等定点到动点E的距离均存在最小值.这里选择最特殊也是最简单的原点O进行探究.显然，当OE⊥BE时，OE长度最小.

2.3.2 明晰主次，以动带动

直角坐标系的作用在于通过坐标与线段长度的相互转化，将图形问题代数化或将数量关系图形化，从而有利于问题解决.但观察“一稿”发现：直角坐标系对问题解决没有发挥作用，有“为坐标系而坐标系”之嫌.若再给出图形中某些运动的元素，从而导致其他元素随之运动，这种主变量与因变量关系可以让直角坐标系成为理想的探究工具.

由于在AC上一定存在点P，使得△CPD≌△COE，此时PD⊥x轴（或PD∥y轴）.若添加该条件，则由线段AC，OC确定从而点P的位置也唯一确定，只要满足CP=CO即可，可这样的话问题的探究价值就打了折扣.遂改变思路：保持PD⊥x轴不变，将点P设为主动点，由点P在AC上运动导致点D在AO上运动，这时点D成了从动点，再给出等边三角形CDE的条件.为引导问题代数化思考，条件中给出动点P的横坐标为m.这既使图形“动”了起来，让直角坐标系有了用武之地，又减少了问题的干扰元素、增加了问题的思维含量.这种变化具有生成性，更加顺畅自然.至此二稿形成.

二稿 如图8，在平面直角坐标系xOy中，△ABC是等边三角形，点A在x轴上，点B，C在y轴上，AC=4，点P为线段AC上一个动点（与点A、C不重合），橫坐标为m.过点P作PD⊥x轴，垂足为D，以线段CD为边向右下方作等边△CDE，连接OE，BE.

（1）当m为何值时，△CPD≌△COE;

（2）在点P运动的过程中，

①∠CBE的大小是否发生变化？若不变，请求出∠CBE的度数;若变化，请说明理由;

②若点E刚好落在x轴上，求此时m的值;

（3）求OE长度的最小值.

2.3.3 适当铺垫，合理优化

深入思考后发现：二稿的问题（1）中△CPD≌△COE的条件是CP=CO=2，此时点P恰为AC中点，过于特殊化，没有体现“任意与变化”的意图，使几何推理与代数运算的命题立意落空，故从3个方面进一步优化.

优化一：变特殊图形为一般图形.将两个等边三角形改为两个顶角相等的等腰三角形，其中AC=5，OC=3.这样，要求出m值必须先用m的代数式表示PD的长，进而转化为求点P的纵坐标.

优化二：在“求点P的横、纵坐标关系”上思考.这种关系可由三角形相似得到，也可根据一次函数关系求得.但由于八年级学生没有研究相似图形，故设置“求AC所在直线的函数表达式”的问题，一方面便于点P的纵坐标的表示，为后续问题的解决搭建脚手架;另一方面符合考查“一次函数”知识的内容目标.

优化三：将重复问题适当合并.由于问题（2）②与问题（3）都属于点E在运动过程中的两个特殊位置，故将两个问题合并为“求OE长度的取值范围”这样一个问题.

通过优化，“三稿”呼之即出.

三稿 如图9，在平面直角坐标系xOy中，△ABC是等腰三角形，AC=BC，点A在x轴上，点B，C在y轴上，A（-4，0）、C（0，3），点P为线段AC上一动点（与点A、C不重合），过点P作PD⊥x轴，垂足为D，以线段CD为边向右下方作等腰△CDE，且满足∠DCE=∠ACB，CD=CE，连接OE、BE，设点P的横坐标为m.

（1）求经过点A，C的直线的函数表达式;

（2）当m为何值时，△CPD≌△COE;

（3）点P在运动的过程中，

①∠CBE的大小是否发生变化？请说明理由;

②求OE长度的取值范围.

2.3.4 删繁就简，简中求道

反复研究发现，三稿中仍有4处值得推敲：一是图形无效线段多，解决问题时用到的∠DCE=∠ACB、CA=CB、CD=CE与线段AB，DE无关;二是直接呈现点B的坐标导致问题（3）①思维含量降低，没有达到压轴题的预期难度;三是条件的语言不够精炼.如“△ABC是等腰三角形”与“AC=BC”重复，“点A在x轴上，点C在y轴上”与“A（-4，0）、C（0，3）”重复;四是“求OE长度的取值范围”过程复杂，可以通过“几何直观”加“适当运算”得到，不必让学生因书写而花费太多时间.综合以上因素，最终决定删繁就简：一是精简图形结构.去掉图9中的线段AB，DE，BE，让图形变得简洁;二是精细呈现方式.将问题（3）①改为让学生探究图9中点B的存在性，在图形运动中探究不变关系;三是精炼数学语言.将“△ABC是等腰三角形，AC=BC，点A在x轴上，点B、C在y轴上，A（-4，0）、C（0，3）”这段文字压缩为“点A、C的坐标分别为（-4，0）、（0，3），连接AC”;四是精减解答要求.将“求OE长度的取值范围”精减为“直接写出OE长度的取值范围”，并适当调整图形的字母，最终形成第四稿（见真题）.

显然，第四稿删除了杂乱且与考查内容无关的信息和繁琐的解题过程要求，图形结构更简洁、语言表达更简约、问题设置更合理、解题过程更顺畅.3 命题感悟

试题命制的曲折过程让笔者充分感受到命题的艰辛与困苦，也享受命题成功的愉悦与惬意，同时还深切感悟到：数学压轴题的命制要立意先行，聚焦目标的指向性;源于教材，着眼问题的发展性;立足基础，注重试题的创新性;关注本质，追求试题的关联性;简约精致，彰显试题的人文性.

3.1 立意先行，聚焦目标的指向性

试题的命制经常经历“立意—形散—神聚”的过程.命题立意是试题之魂，决定了试题的意境与层次.该试题在命制之初就明确了命题立意.从考查目标上说，就是立足基础、着眼发展、关注能力、指向素养，如考查数学探究的能力与思想方法的感悟;从命题方式上说，就是源于教材、有效关联、力求创新、适当综合，如考查三角形全等与相似、直角三角形相关性质、直角坐标系的综合与联系.

3.2 源于教材，着眼问题的发展性

许多优秀试题都源自于教材.教材与试题的依据都是课程标准，二者可谓“同源同宗”.数学命题要“重视教材例习题的的作用，引导学生回归课本和知识本源，从数学教材中探‘源’——问题的源头与原型，充分挖掘教材例题的价值;从数学本质上寻‘宗’——揭示问题与教材、问题与问题之间的内在联系”[2].如果善于从教材中寻找命题灵感，通过改变问题背景、改变条件或结论、变换设问方式，关联其他问题等手段，就能命制出“神形兼备”与“神形皆变”的试题.另外，一道好的试题不仅应该有试场效应，还应该具有深远的发展价值、有继续研究与思考的空间.

该题就是从课本习题入手，通过改变图形的位置，增加平面直角坐标系的背景，并将静态问题动态化处理，利用运动变化中不变的图形关系设计层次分明的问题，既考查学生对三角形全等、勾股定理和一次函数等基础知识的掌握，也考查了学生动态探究的能力以及对“数形结合”“变中不变”等数学思想方法的感悟.

从发展角度来看，一是利用教材问题的发展性.教材中的例习题及相关素材都是精心选择与设计的，既是教材的资源与母体，也是命题的素材与原型，深入研究教材的编写意图，挖掘教材资源的内涵，可以让教材在教学与命题中走得更远.以教材这道题为例，通过命题者的精心设计，发展成了一道试卷的压轴题.二是试题本身也具有发展性.最终呈现在试卷上的试题只是诸多设想中的一部分.例如：本题还可以求探索以下问题：（1）动点D到点A，B距离之和的最小值;（2）是否存在点P，使点C，P，B，D在同一圆上……

所以，深入研究并利用教材资源的发展性编制试题，是提升试题命制能力的灵丹妙药.

3.3 立足基础，注重试题的创新性

作为学习评价的重要载体与依据，数学命题要在“立足基础”与“适度创新”之间平衡.一方面，要立足基础，拒绝怪题、偏题，引导教师重视数学的基础知识、基本技能、基本思想、基本活动经验的教学，避免陷入题海战，减轻学生过重的作业负担.另一方面，要适度创新，激发学生探究欲望，促进学生在掌握通性解法的基础上发展创新思维、强化创新意识，防止走进机械模仿和套路化的“死胡同”.

该题体现了立足基础与适度创新有机结合的特点.试题立足基础，将全等三角形的性质与判定、勾股定理、直角坐标系、一次函数等基础知识融于一题，体现了对方程与代数化、坐标与长度的相互转化等基本方法的考查.同时试题又有所创新.如第（3）问“在y轴上是否存在一点E，使得∠BED的大小始终不发生变化？”这种对存在性问题设问方式新颖独特，激发了学生的探究欲望，是试题的创新所在、活力所在、精彩所在.

3.4 关注本质，追求试题的关联性

数学教学与命题“要推动学生的学习认知从感性走向知性和理性，即从表面的模糊的认识走向事物联系和事物本质的把握和判断，从外部的操作感知走向内部的理解认知”[1].如果命题是建筑，那么立意只能是“画在图纸上的大厦”;如果命题是烹饪，即使有足够的食材，也不一定变为色香味俱佳的美食.命题还需要实际操作，包括素材选择、结构谋划、逻辑推敲、语言组织等.在这个过程中，最重要的是从看似杂乱无章、纷繁杂乱的问题中寻找灵感，发现相互间的内在联系，从而抓住问题的本质.命题者要善于挖掘“不相干”信息之间的内涵与联系，以这种联系为纽带将“散乱”的信息加以整合、结构化，从而产生“意外”的惊喜与收获.

本题经历了素材选取与变化、問题发展与变式、结构重组与优化的过程：从“双等边三角形”的素材选取到“双等腰三角形”的合理变化;从对运动中某些“特殊位置的数量关系”的探究与思考到对“整个运动过程中动点路径”的寻找与计算;从“三角形全等存在性”的探索与确认到“角大小不变性”的猜想与验证，将图形运动、图形全等、图形与坐标等关键要素联系在一起，从而命制出本真而又灵动的试题.

由此可见：对问题内在联系的洞察、对数学本质的把握、对试题本真的追求是命制高质量试题的关键.

3.5 简约精致，彰显试题的人文性

“简约而不简单”是一种命题能力、一种命题境界，更是一种命题情怀.比如，命题中删除图形中不必要的线条，使图形结构更加简洁;删除重复、冗长的文字，使语言表达更精炼，都体现了“简约精炼”的命题特色.同时，给出的备用图方便学生对图形不同位置的探究;最后一问改为直接写结果，适度降低答题要求，便于学生利用几何直观得到结论，避免繁琐的书写过程，这些都彰显了命题者对学生的人文关怀.

参考文献

[1]罗建宇.从融合到创新：基于GeoGebra的数学深度教学[J].数学通报，2020（02）：23.

[2]钱德春.回归迁移优化发展——对一道几何填空题探究历程的启示与思考[J].中学数学杂志（初中），2016（02）：41-44.

作者简介 钱小强（1981—），男，江苏泰州人，副校长，中学高级教师;市学科带头人，获省初中数学青年教师基本功比赛一等奖、省教学成果二等奖、市初中数学优秀课一等奖，三次参加泰州市中考命题;主要研究初中数学教学与命题.

钱德春（1963—），男，江苏泰州人，中学高级教师;江苏省中学数学专业委员会理事，省初中数学名师共同体导师，泰州学院特聘教授，中国人民大学《复印报刊资料·初中数学教与学》编委，《义务教育数学课程标准（2022年版）》教学要求编写组成员;主要从事初中数学教学、命题与教师专业发展等研究.