THE ∂-LEMMA UNDER SURJECTIVE MAPS*

Lingxu MENG (孟令旭)

Department of Mathematics，North University of China，Taiyuan 030051，China

E-mail:menglingxu@nuc.edu.cn

Abstract We consider the∂-lemma for complex manifolds under surjective holomorphic maps.Furthermore，using Deligne-Griffiths-Morgan-Sullivan’s theorem，we prove that a product compact complex manifold satisfies the∂-lemma if and only if all of its components do as well.

Key words ∂-lemma;surjective holomorphic map;product complex manifold;fiber bundle;E1-isomorphism

1 Introduction

In this paper，all complex manifolds are assumed to be connected.

The∂-lemma on a compact complex manifoldXrefers to the fact that for every pure-typed-closed form onX，the properties ofd-exactness，∂-exactness，-exactness and∂-exactness are equivalent，while a compact complex manifold is called a∂-manifold if the∂-lemma holds on it.The most well-known examples of this are compact Kähler manifolds.All complex manifolds in the Fujiki class C are∂-manifolds[7]and not Kählerian in general.There also exist many examples which are not in C;see[2–4，10].In particular，D.Angella，T.Suwa，N.Tardini and A.Tomassini[4]provided an example which is simply-connected.R.Friedman[8]recently proved that the∂-lemma holds on general Clemens manifolds.

The real homotopy type of a∂-manifold is a formal consequence of its de Rham cohomology ring[7]，which is a strong topological obstruction of the∂-lemma property.D.Angella，N.Tardini，A.Tomassini[5，6]gave criterions of∂-manifolds by non-Kählerness degrees.The∂-lemma property is stable under small deformations of the complex structure[6，18，19].Recently，an important result showed that the blow-up of a compact complex manifold along a complex submanifold is a∂-manifold if and only if the complex manifold and the complex submanifold are both∂-manifolds[4，11–14，16，20].This implies that the heredity and bimeromorphic invariance of the∂-lemma property are equivalent.

Recently，J.Stelzig[14–16]deeply investigated the structure of bounded double complexes.TheEr-isomorphism between double complexes is a central notion in his works.In particular，theE1-isomorphism is very useful for the study of various cohomologies and the∂-lemma property.We consider theE1-isomorphism under surjective holomorphic maps and apply it to the∂-lemma property as follows:

Theorem 1.1Letf:X→Ybe a holomorphic map between compact complex manifolds withr=dimCX-dimCY.Assume that there exists a closed (r，r)-currentTonXsuch thatf*T0.Then，

(2)Δ(X)≥Δ(Y);

(3) ifXsatisfies the∂-lemma，Yis a∂-manifold.

Some applications of Theorem 1.1 will be given in Section 3.Furthermore，we study the∂-lemma on product complex manifolds.

Theorem 1.2LetXandYbe compact complex manifolds.ThenX×Ysatisfies the∂-lemma if and only ifXandYdo.

2 Preliminaries

2.1 Real structure

For an injective complex linear mapφ:U→Vof complex vector spaces，Ucan be viewed as a complex subspace (i.e.，φ(U)) ofVviaφ.Suppose thatU1，...，Un，Vare complex vector spaces and thatφ:is an isomorphism，whereUiis an external direct sum ofU1，...，Un.Thenis an internal direct sum of subspaces.We simply write these asUi，which is said to be the direct sum of the subspacesU1，...，Unviaφ.

If there exists a real vector spaceKsuch thatU=K⊗RC，we say thatUis a complex vector space with real structure.A complex linear mapφ:U→Vof complex vector spaces is said to be real if it is the complexification of a real linear map of real vector spaces，namely，φ=ψ⊗id:U=K⊗RC→V=L⊗RC for a (real) linear mapψ:K→Lof real vector spaces.For example，Hk(X，C)=Hk(X，R)⊗RC is a complex vector space with real structure for a smooth manifoldXand the pull backf*:Hk(Y，C)→Hk(X，C) is real for a smooth mapf:X→Yof smooth manifolds，since it is the complexification off*:Hk(Y，R)→Hk(X，R).Assume thatφ:U→Vis injective and real.We viewUas a complex subspace ofV，while the complex conjugationof the complex subspaceW⊆Ucan be viewed as the one ofφ(W) inVviaφ，since.Suppose thatUandVare complex vector spaces with real structures.ThenU⊗CVhas a natural real structure，under which the complex conjugationofα⊗βinU⊗CVis just¯α⊗¯βforα∈Uandβ∈V.

2.2 Double complex and related structures

Regarding the concepts of this subsection，we refer to[16，Section 2]for more details.

Let (K·，·，∂1，∂2) be a double complex with two endomorphisms∂1，∂2of bidegree (1，0) and (0，1)，which satisfy that∂i°∂i=0 fori=1，2 and∂1°∂2+∂2°∂1=0.For convenience，we sometimes briefly write this asK·，·.A double complexK·，·is said to be bounded ifKp，q=0，except for finitely many (p，q)∈Z2.

From now on，all the double complexes mentioned are assumed to be of vector spaces over C and bounded.For a double complexK·，·，let:Kp，q→Kp+1，qand:Kp，q→Kp，q+1be the restrictions of∂1and∂2，respectively.Recall the following constructions:

·The de Rham cohomology

where (K·，d=∂1+∂2) is the simple complex associated toK·，·.

·The row and column cohomologies

·The Bott-Chern and Aepplicohomologies

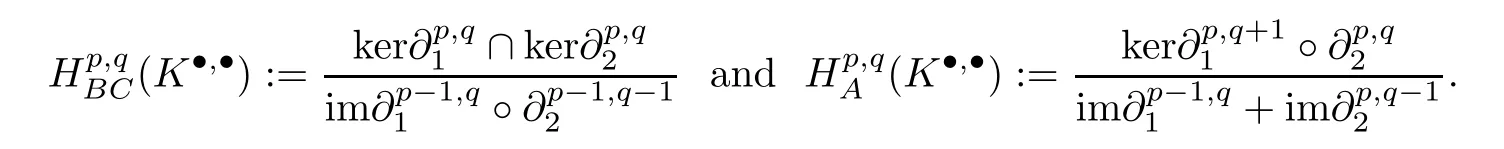
·The filtration by columns

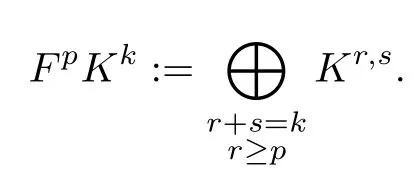
This filtration onK·induces the one on(K·，·)，i.e.，the (first) Hodge filtration on the de Rham cohomology.We get the so called (first) Frlicher spectral sequence forK·，·，denoted bySet

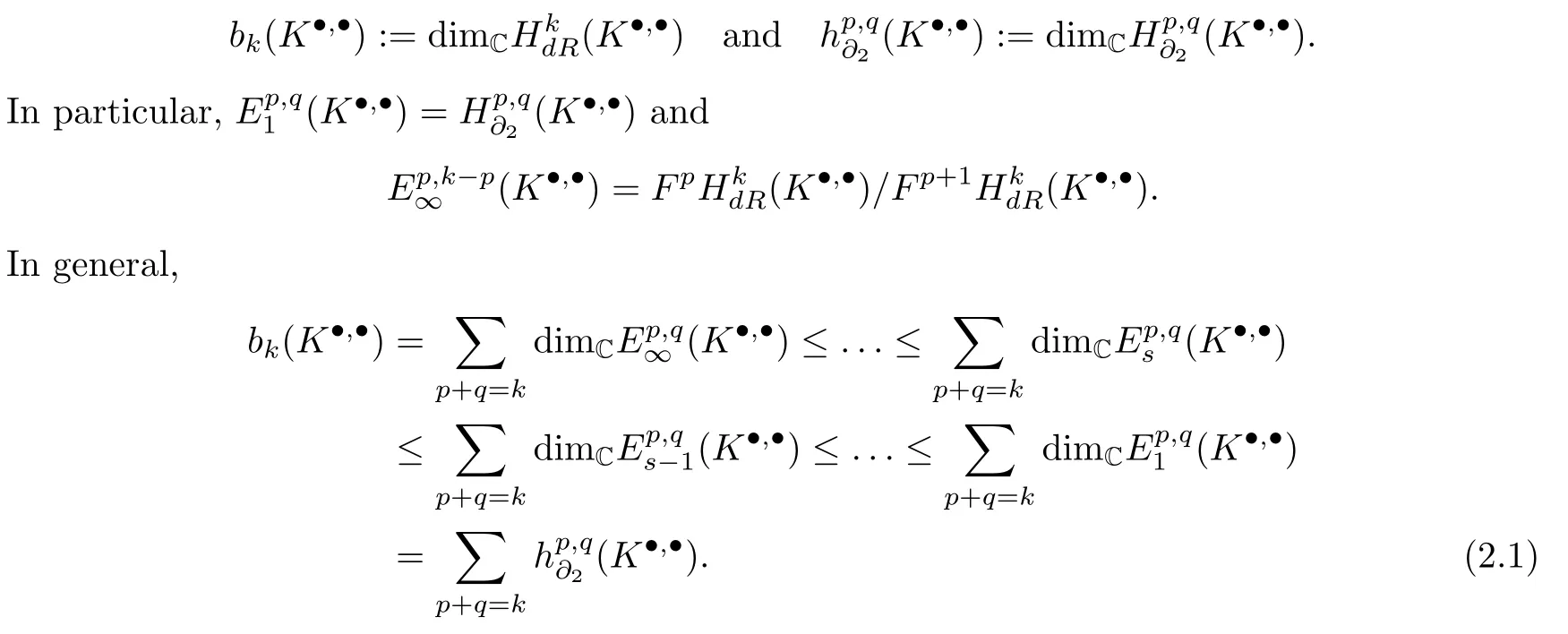
Suppose thatXis a compact complex manifold.Denote byAp(X)C，Ap，q(X)，Dp，q(X) andHk(X，C) the spaces of complex valued smoothp-forms，smooth (p，q)-forms，(p，q)-currents and the de Rham cohomology with complex coefficients onX，respectively.The double complexes (A·，·(X)，∂，) and (D·，·(X)，∂，) are bounded.Thenbk(X):=bk(A·，·(X)) andhp，q(X):=are just thek-th Betti and (p，q)-th Hodge numbers，respectively.Denote by，FpHk(X，C)) the Frlicher spectral sequence forA·，·(X).Thenand

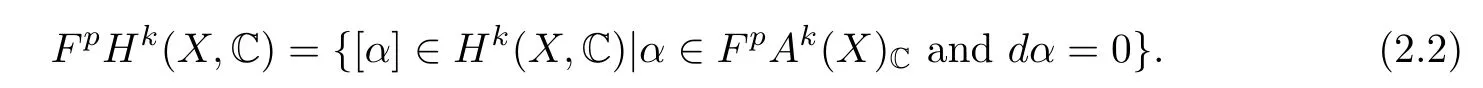
Denote byk(X，C) the complex conjugation of the subspaceFqHk(X，C) inHk(X，C).Setforp+q=k.We say that the Hodge filtration gives a Hodge structure of weightkonHk(X，C) if

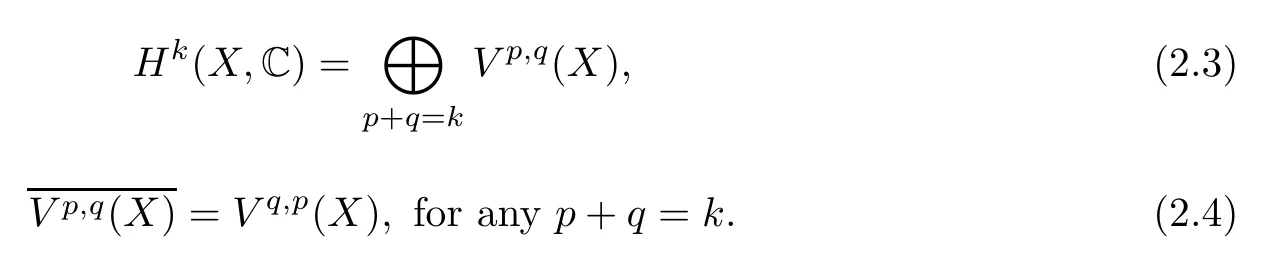
P.Deligne，P.Griffiths，J.Morgan and D.Sullivan established the following well-known theorem on the relationship between the∂-lemma and the Frlicher spectral sequence:

Theorem 2.1([7，(5.21)]) For a compact complex manifoldX，the following statements are equivalent:

(i) The∂-lemma is true forX.

Remark 2.2In Theorem 2.1，we have that

(1)(ii)(a) is equivalent to the fact that(X) for allkandp，and hence is equivalent to the fact thatfor allk.

(3) For a∂-manifoldX，

If a morphism of double complexes induces isomorphisms on all column cohomologies (i.e.，induces an isomorphism atE1between Frlicher spectral sequences)，then it also induces isomorphisms on all de Rham cohomologies.A morphism of double complexes is called anE1-isomorphism if it induces isomorphisms on all row and column cohomologies.We say thatK·，·≃1L·，·，if there exists anE1-isomorphismK·，·→L·，·.Then≃1is an equivalence relation by[14，Lemma 1.24](or[16，Proposition 11]).Set

By the definition，Δ(·) is additive for direct sums.Assume thatK·，·≃1L·，·.Thenbk(K·，·)=bk(L·，·).By[16，Corollary 13]，Hence，Δ(K·，·)=Δ(L·，·).

For a compact complex manifoldX，the inclusionis anE1-isomorphism，i.e.，A·，·(X)≃1D·，·(X).Set Δ(X):=Δ(A·，·(X)).D.Angella，A.Tomassini[6，Theorems A and B]and J.Stelzig[16，Theorem 9]proved

Theorem 2.3For any bounded double complexK·，·，Δ(K·，·)≥0.Moreover，a compact complex manifoldXsatisfies the∂-lemma if and only if Δ(X)=0.

3 An E1-Isomorphism Under Surjective Maps

Consider the holomorphic mapf:X→Ybetween compact complex manifolds withr=dimCX-dimCY≥0 satisfying that

(⋆) there exists a closed (r，r)-currentTonXsuch thatf*T0.

Notice that any map satisfying (⋆) is surjective.If this were not the case，by the proper mapping theorem，f(X) would be an analytic subset inYwith dimension＜dimCY.For a general pointo∈f(X)，Xo=f-1(o) has dimension dimCX-dimCf(X)＞r.The natural mapinduced by the inclusion is an isomorphism，so there exists a closed smooth (r，r)-form Ω onXsuch thatT=Ω+∂Sfor someS∈Dr-1，r-1(X).Thenf*T=f*Ω=∫XoΩ|Xo=0，which contradicts (⋆).

Example 3.1Letf:X→Ybe a surjective holomorphic map between compact complex manifolds withr=dimCX-dimCY≥0.The condition (⋆) is satisfied in the following cases:

(1)fis a Kähler morphism;

(2)Xis ar-Kähler manifold;

(3) dimCX=dimCY，i.e.，r=0;

(4)Xis a Kähler manifold;

(5) there exists an analytic subsetZofXwith codimensionrsuch thatf(Z)=Y.

Recall that a morphismf:X→Yof complex spaces is said to be a Kähler morphism if there exists an open covering U={Uα}ofXand a system of smooth functions{pα∈C∞(Uα)}satisfying that the restrictionpα|Uα∩Xyis a strictly plurisubharmonic function for everyy∈Y，andpα-pβis a pluriharmonic function onUα∩Uβ∩Xyfor everyα，β，whereXy=f-1(y) is the fiber offovery(c.f.[9，Definition 4.1]).Evidently，gives a real closed (1，1)-formωfglobally defined onXand the restrictionωf|Xyis a Kähler form onXyfor everyy.We call such anωfthe relative Kähler form off.In (1)，the constantfor any regular valueyoff.A complex manifoldXis calledp-Kählerian if it admits a closed transverse (p，p)-form Ω(c.f.[1，Definition 1.1，1.3]).In such a case，Ω|Zis a volume form onZfor any complex submanifoldZof pure dimensionpofX.In (2)，there exists a closed transverse (r，r)-form Ω onXand the constantfor any regular valueyoff.Any complex manifold is 0-Kählerian and any Kähler manifold isp-Kählerian forpsmaller than its dimension，so (3) and (4) are special cases of (2).In (5)，denote byTZthe current defined by the integral onZ.ThenTZis a closed (r，r)-current onXandf*TZ=d＞0，wheredis the general multiplicity ofZoverY.

We generalize[14，Lemma 1.38](or[15，Lemma 7]) as follows:

Lemma 3.2Letf:X→Ybe a holomorphic map between compact complex manifolds withr=dimCX-dimCY.Assume that there exists a closed (r，r)-currentTonXsuch thatf*T0.Then

is anE1-isomorphism.Moreover，

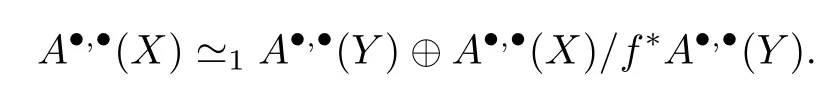
ProofFix an integerp.Denote byAp，·(X)，A·，p(X)，Dp，·(X) and D·，p(X) the complexes (Ap，·(X)，)，(A·，p(X)，∂)，(Dp，·(X)，) and (D·，p(X)，∂)，respectively.By assumption，c=f*Tis a nonzero constant.By the projection formula，

for everyα∈A·，·(Y)，which implies thatf*is injective.Hence，there is a short exact sequence

of double complexes，which induces a long exact sequence

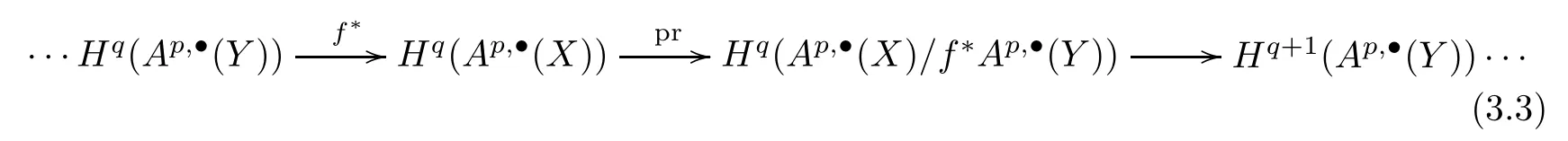
for anyp.By (3.2)，the composition

is the left inverse map off*.For allpandq，we obtain split exact sequences

from (3.3)，which implies that (3.1) induces isomorphisms on column cohomologies.Similarly，

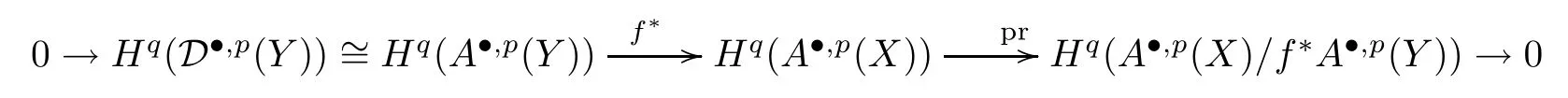
are split exact sequences for allpandq，and the composition

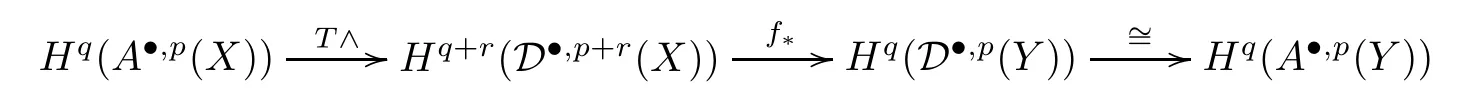
is the left inverse map off*，which implies that (3.1) induces isomorphisms on row cohomologies.Thus (3.1) is anE1-isomorphism.SinceA·，·(Y)≃1D·，·(Y)，we get the second conclusion.□

Now，we give a proof of Theorem 1.1 as follows:

Proof of Theorem 1.1Assume that the Frlicher spectral sequence degenerates atEsforX.Then(X) for allk.We have

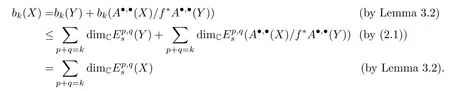
Thusbk(Y) for allk，which implies that the Frlicher spectral sequence degenerates atEsforY.By Lemma 3.2，Δ(X)=Δ(Y)+Δ(A·，·(X)/f*A·，·(Y)).By Theorem 2.3，(2) follows.Suppose thatXis a∂-manifold.By (2) and Theorem 2.3，we easily get (3).Here，we give a more direct proof.Letαbe a (p，q)-form onYsuch thatα=dβfor someβ∈Ap+q-1(Y).Thenf*α∈Ap，q(X) satisfies thatf*α=d(f*β).SinceXis a∂-manifold，f*α=∂γfor someγ∈Ap-1，q-1(X).For the nonzero constantf*Ω，setc=f*Ω.By the projection formula，

We study the∂-lemma on fiber bundles.

Proposition 3.3Letπ:E→Xbe a holomorphic fiber bundle over a compact complex manifoldX，whose fibers are compact complex manifolds.Assume that there exist closed formst1，...，trof pure bidegrees satisfying that the restrictions of Dolbeault classestoExis a linear basis offor everyx∈X.Then we have the following:

(2) If the∂-lemma holds onE，then it also holds onX.

(3) Suppose that the restrictions of Dolbeault classestoExis also a linear basis of(Ex).Denote by (u1，v1)，...，(ur，vr) the degrees oft1，...，trrespectively.Then

is anE1-isomorphism and Δ(E)=r·Δ(X).Moreover，the∂-lemma holds onEif and only if it holds onX.

ProofWrite (3.4) asτ:K·，·→A·，·(E).Between the two double complexes，τinduces isomorphisms atE1-pages

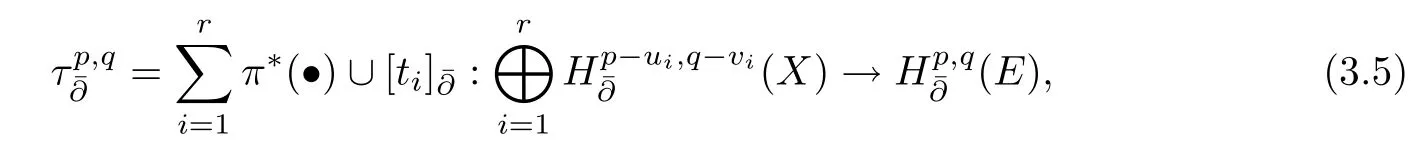
by[11，Theorem 1.3]，hence it induces isomorphismsatEs-pages and isomorphismsatH-pages.

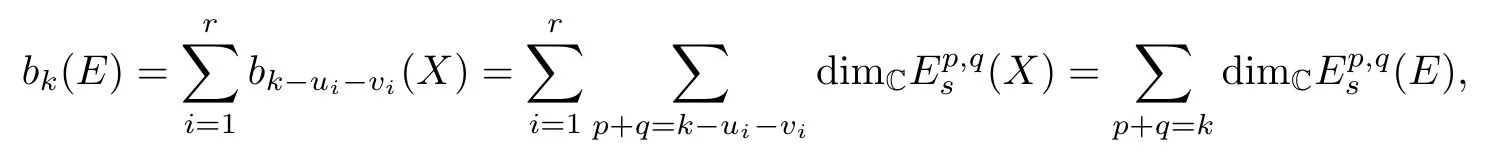
Denote byuthe complex dimension of the fiber ofE.Fix a pointx∈X.By the hypothesis，there is sometisuch thatis the generator of.Thenui=vi=uandBy Theorem 1.1(1)(3)，the other half of (1) and (2) follows.

Consider the commutative diagram

Remark 3.4In the previous work，we proved Proposition 3.3(3) under a stronger assumption;see[11，Theorem 5.5].

Remark 3.5The flag bundles satisfy the assumptions in Proposition 3.3(3);see[11，Corollary 5.7].

Remark 3.6Fix an integern.The following two statements are equivalent:

(1) The∂-lemma property is bimeromorphic invariant in the category of compact complex manifolds of dimensionn.

(2) The∂-lemma holds on compact complex manifolds of dimensionnwhich are meromorphic images of∂-manifolds of dimensionn.

Assume that (1) holds.Suppose thatXsatisfies the∂-lemma and thatis a surjective meromorphic map between compact complex manifolds of dimensionn.Any desingularizationZof the graph offis a∂-manifold，since it is bimeromorphic toX.The map fromZontoYsatisfies (⋆)(see Example 3.1(3))，soYsatisfies the∂-lemma by Theorem 1.1(3).Hence (2) holds.The other part obviously follows.

In general cases，the bimeromorphic invariance of the∂-lemma property is still an open problem;see[4，13，14，16，20].S.Yang and X.-D.Yang[20，Theorem 1.3]proved that the∂-lemma property is bimeromorphic invariant in the category of threefolds.Hence，the∂-lemma holds on the threefolds which are meromorphic images of∂-threefolds.

4 The∂-Lemma on Product Complex Manifolds

Lemma 4.1Suppose thatXandYare compact complex manifolds.For anys≥1，the Frlicher spectral sequence degenerates atEsforX×Yif and only if it degenerates atEsfor bothXandY.

ProofAs with those in the proof of Proposition 3.3(3)，it is easy to prove that the external productA·，·(X)⊗CA·，·(Y)→A·，·(X×Y) is anE1-isomorphism，by the algebraic Künneth theorem and the Künneth theorem for Dolbeault cohomology，whereA·，·(X)⊗CA·，·(Y) is the double complex associated toA·，·(X) andA·，·(Y).Thus，for anys≥1，，and then

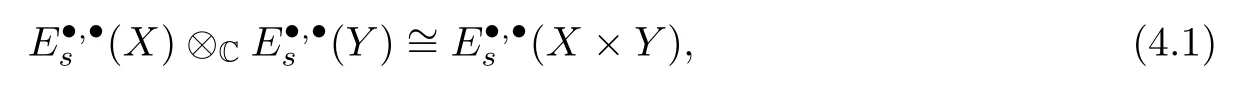
by[16，Lemma 15].We have

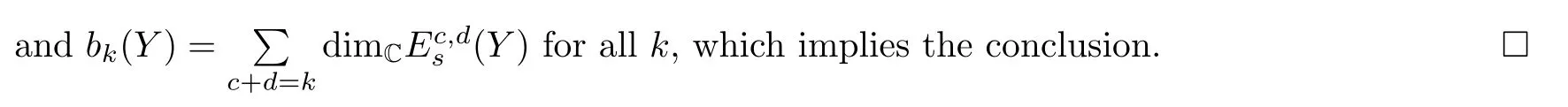
Now we give a proof of Theorem 1.2 as follows:

Proof of Theorem 1.2Let pr1and pr2be the projections ofX×YontoXandY，respectively.

Suppose thatX×Yis a∂-manifold.Fix a pointy∈Y.Clearly，pr1has a multisectionX×{y}，so it satisfies (⋆)(see Example 3.1(5)).By Theorem 1.1(3)，Xsatisfies the∂-lemma.Similarly，the∂-lemma holds onY.

Suppose thatXandYare both∂-manifolds.By Theorem 2.1 and Lemma 4.1，it is sufficient to check the following:

ClaimThe Hodge filtration gives a Hodge structure of weightkonHk(X×Y，C) for everyk≥0.

Denote byφboth the external productsand.Viaφ，we have the direct sum decomposition

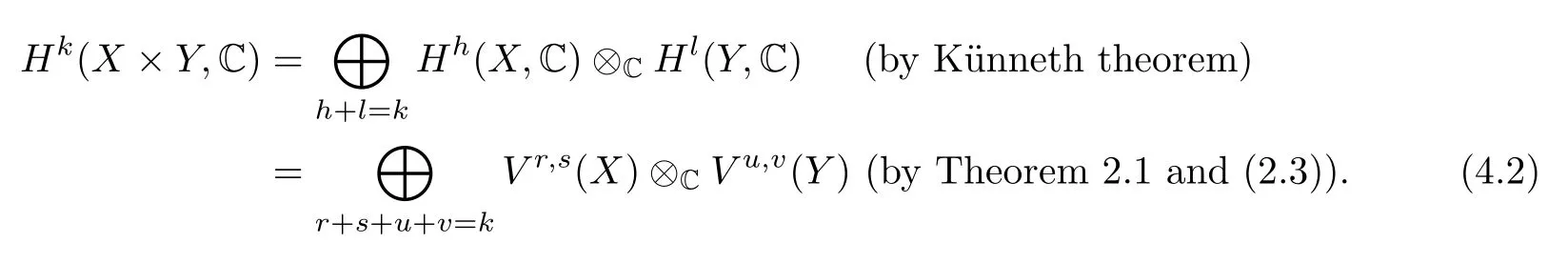
Fora+b=p，h+l=k，FaAh(X)C⊗CFbAl(Y)Cis mapped intoFpAk(X×Y)Cbyφ，which implies thatFaHh(X，C)⊗CFbHl(Y，C)⊆FpHk(X×Y，C) viaφby (2.2).For convenience，FpHk(X×Y，C) will shortly be written asFpHk.Then

AllVr，s(X)⊗CVu，v(Y) are direct summands in the decomposition (4.2) ofHk，so the last sum in (4.3) is a direct sum.Hence

For anyp，we have an (non-canonical) isomorphism

and then an (non-canonical) isomorphism

From (4.2) and (4.6)，the sumof complex subspaces inHk(X×Y，C) is just the direct sumVp，q(X×Y) and

Clearly，φis real，soVp，q(X×Y)=Vq，p(X×Y)，by (4.6).We have proved the claim.

Remark 4.2For the part of“only if”，we can also give a direct proof.Suppose thatX×Ysatisfies the∂-lemma.Denotem=dimCYand let ΩYbe a closed smooth (m，m)-form onYsuch that its Dolbeault class is the inverse image of 1 under the isomorphismRSetClearly，Ω isd-closed.The constant

for anyx∈X.By Theorem 1.1(3)，Xis a∂-manifold.Similarly，Ysatisfies the∂-lemma.

Remark 4.3By Proposition 3.3(3)，we have given another proof of that in the previous work[11，Corollary 5.8].

AcknowledgementsThe author warmly thanks Sheng Rao，Song Yang，Xiang-Dong Yang and Jonas Stelzig[17]for useful discussions.