受参数激励屈曲梁的次谐分岔和混沌运动

张冬梅 李锋

(临沂大学数学与统计学院,临沂,276000)

1 Introduction

The arch structures have wide amplifications in aerospace and engineering. The flexible buckled beam as arch like structures may display a wealth of phenomena including subharmonic oscillations, period bifurcations, chaotic vibrations and so on. Therefore it is of great significance to investigate nonlinear dynamics of the system. A lot of results about bifurcation and chaotic motions for buckled beam models have been obtained in the past two decades. Moon and Holmes[1]detected the chaotic motions of buckled beam under external harmonic excitations. Abou Rayan [2] investigated the nonlinear dynamics of a simply supported buckled beam and obtained a sequence of supercritical period doubling bifurcations.Ramu et al. [3] used a single mode approximation to study the chaotic motion of a simply supported buckled beam. Reynolds and Dowell [4] explored the chaotic motion of a simply supported buckled beam under a harmonic excitation by using the Melnikov theory. Emam and Nayfeh [5] investigated the global dynamics of a clamped clamped buckled beam subjected to primary resonance excitation. They obtained the stability and bifurcations of the periodic orbits by using the floquet theory. Oumarou et al.[6]investigated the appearance of horseshoes chaos on the dynamics of a buckled beam under the control of distributed couple forces applied at different points. Emam and Abdalla [7] presented the nonlinear response of simply supported buckled beams subjected to a subharmonic parametric resonance. They found that the second and higher modes have no contribution on either the static or the dynamic response of the beam.

The Melnikov method is an effective technique in the study of nonlinear dynamics systems. This method allows one to predict chaos in nearly Hamiltonian system with homoclinic or heteroclinic orbits.A lot of achievements have been obtained for the chaotic behaviors of many dynamic models, such as a class of inverted pendulum system [8], a parametrically excited cantilever beam [9], a parametrically excited viscoelastic moving belt[10],a laminated composite piezoelectric rectangular plate[11]and a class of planar hybrid piecewise smooth systems [12]. Based on the classical Melnikov method, Marian and Refael[13]developed a global Melnikov theory for the splitting of homoclinic manifolds in Hamiltonian systems subject to time dependent perturbations. Sun et al. [14] improved the subharmonic Melnikov method and used it to investigate the subharmonic orbits of a simply supported rectangular thin plate under the combined parametric and external excitations. Hu and Zhang[15]studied the bifurcation and chaos of thin circular functionally graded plate under one term and two term transversal excitations. They obtained the criteria for the existence of chaos with the Melnikov method. The chaos in subsonic panel has been studied by Tang et al. [16]. Based on the Melnikov method,they suppressed the chaotic motion of the plate by adding a parametric excitation term to the chaotic system. They reported the fully consistent results in their publication and stated that the first order expansion can qualitatively reflect the dynamical features of the plate.

In this paper, the chaotic dynamics for the model of buckled beams is studied analytically with the Melnikov method. The critical curves separating the chaotic regions and non chaotic regions are presented.The results obtained here show that there exist uncontrollable regions in which chaos always take place for the system with linear or cubic parametric excitation. Some complicated dynamical behaviors are obtained for this class of systems.

2 Formulation of the problem

Consider an homogenous elastic beam of lengthL, a mass per unit volumeρ, a cross sectionA, a damping coefficientγ,a moment of inertiaIand modulus of elasticityE. The system is subjected to both parametric and additive forces of magnitudePandQ. After buckling,the resulting static configuration is described byW0(X). At timeT,the new configuration is described byW(X,T),measured fromW0.

Figure 1 The model of the buckled beam

The nonlinear differential equation of the buckled beam is given as[6]

For a simply supported structure,by introducing the dimensionless quantities,Eq. (2.1)becomes

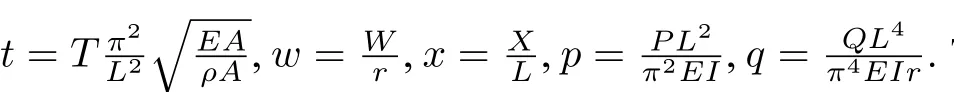
whereα= 1−p0andp0is the static axial load,F0andωare respectively the amplitude and frequency of the axial excitation,q0and Ω are respectively the amplitude and frequency of the additive excitation.

Assume the damping and excitation termsγ,q0are small, and letγ=∊γ,q0=∊q0, where∊is a small parameter,then Eq. (2.3)can be written as

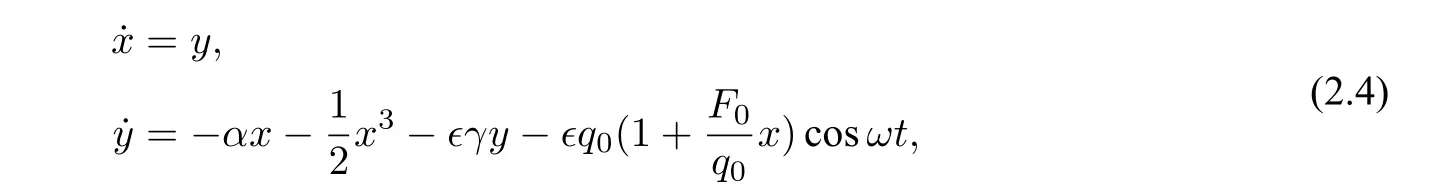
wherex=a. For convenience,settingη=,β=q0,thus Eq. (2.4)is reduced to

when∊=0,the unperturbed system is

which is a planar Hamiltonian system with the Hamiltonian

Figure 2 The phase portrait of system(3.3)

3 Chaotic motions of the system

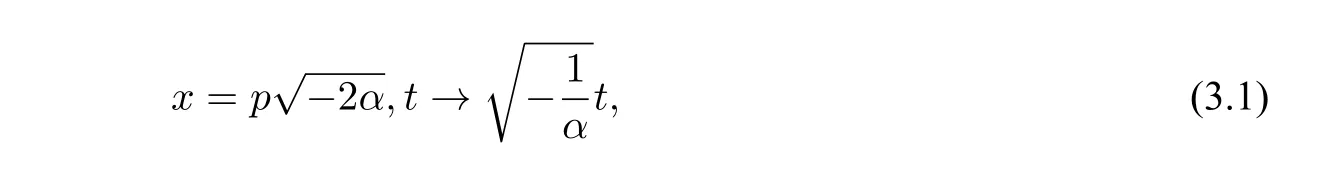
Whenα<0,using the transformations and substituting(3.1)into(2.4)yields

System(3.3)has three equilibrium points,where(0,0)is a saddle point,and(±1,0)are all centers.The phase portrait of system(3.3)is shown in Fig. 2.

The expressions of homoclinic orbits which connected(0,0)to itself are given by

There exist closed periodic orbits around(±1,0)with the expressions

wheresn,dn,cnare the Jacobi elliptic functions, andkis the modulus of the Jacobi elliptic functions.

The period of the closed orbit isTk=2,whereK(k)is the complete elliptic integral of the first kind.

In this section,the Melnikov method[17]is used to investigate the chaotic motions of system(3.2).

The Melnikov function of system(3.2)along the homoclinic orbits is computed as follows

where

By Melnikov analysis,the condition for transverse intersection and chaotic separatrix is obtained as follows

Whenη= 0, there only exists one periodic external excitation. By selecting different values ofα,α=−0.25,α=−0.6,α=−1,α=−1.2, we may obtain the critical curves separating the chaotic regions and non chaotic regions which are shown in Fig. 3(a). For the case of periodic external excitation,the critical curves have classical bell shape. When the excitations possess sufficiently small or very large periods, the systems are not chaotically excited. For the case of small values ofω, the critical value for chaotic motions increases asαincreases. Whenωcrosses a critical value, the critical value for chaotic motions decreases asαincreases.

Whenη=1,there exist both periodic external and parametric excitations. For different values ofα,α=−0.25,α=−0.6,α=−1,α=−1.2,we may also obtain the critical curves as in Fig. 3(b). For the case of both periodic external and parametric excitations,the critical value for chaotic motions decreases when the excitation frequencyωincreases. For sufficiently smallω,the system is prone to chaos,while it exceeds the critical value,the critical value of the chaotic behavior decreases as the excitation frequencyωincreases. There exists a controllable frequencyωat which chaotic motions cannot take place no matter how large the excitation amplitude is.

Figure 3 (a)The critical curves when η = 0 (b)The critical curves when η = 1

4 Subharmonic bifurcations of the system

When

subharmonic bifurcation ofm(odd)orders will occur;when

subharmonic bifurcation ofm(even)orders will occur.

5 Numerical simulations

The numerical approach and the fourth order Runge Kutta algorithm are used to explore the chaotic motions of a shallow simply supported buckled beam. The phase portraits,time history curves and Poincare section of system(2.3)are obtained in this section. When the parameters are chosen asα=−0.6,γ=6.8,η= 1,ω= 2,F0= 0.12,and the initial value(x(0),y(0)) = (1.081,0.001),the phase portraits and the time history ofx(t)are shown in Fig. 4 and the poincare section is shown in Fig. 5. From Fig. 4 and Fig.5,we can see that the system undergo periodic motions. When the parameters are chosen asα=−1.2,γ= 0.02,η= 1,ω= 1,F0= 12 and the initial value is as the same as before,the phase portraits and the time history ofx(t)are shown in Fig. 6,and the poincare section is shown in Fig. 7. The maximum Lyapunov exponent isλ=0.096494. Then we can conclude that the system is chaotically excited in these conditions. So the numerical simulations agree with the analytical results.

Figure 4 (a)The phase portraits of system(2.3) (b)The time history curves of system(2.3)

Figure 5 The poincare sections of system(2.3)for f = 0.12

Figure 6 (a)The phase portraits of system(2.3) (b)The time history curves of system(2.3)

Figure 7 The Poincare sections of system(2.3)for f = 12

6 Conclusions

With the Melnikov method,the subharmonic bifurcations and chaotic motions for the buckled beam model subjected to parametric and additive excitations are investigated. It is proved that the system may be chaotically excited through finite subharmonic bifurcations. The critical curves separating the chaotic and non chaotic regions are also given. Some complicated chaotic dynamical behaviors are presented for this system. The results provide some inspiration and guidance for the analysis and dynamic design of this model. For example,while designing this class of systems,we should choose suitable system parameters which is near the controllable frequency,so that the system is not chaotically excited.