基于RTD可编程逻辑门的n变量函数实现算法

姚茂群，冯杰，刘志强，李聪辉

（杭州师范大学信息科学与技术学院，浙江 杭州 311121）

0 引 言

共振隧穿二极管（resonant tunneling diode，RTD）是一种比较成熟的量子器件，可用来解决传统CMOS电路因工艺尺寸逼近物理极限而出现的热耗散、短沟道效应和量子力学效应等一系列问题[1-4]。RTD具有工作频率高、功耗低、能自锁和负内阻等特性，非常适合数字集成电路设计[5-6]，特别是其负内阻特性，在阈值逻辑电路设计中具有显著优势[7-8]。RTD可编程逻辑门是一类特殊的阈值电路，通过该逻辑门可实现任意的n变量逻辑函数[9]。RTD可编程逻辑门由单双稳态转换逻辑单元（monostable bistable transition logic element，MOBILE）、n个正输入分支以及n个负输入分支组成，其中MOBILE利用RTD设计，是阈值电路的重要逻辑单元[10-13]。由于二进制神经元模型与阈值逻辑门具有一定的相似性，因此可利用二进制神经网络实现任意n变量逻辑函数[14-15]。二进制神经网络由输入层、隐层和输出层三层网络结构组成[16]。文献[9]和文献[17]均基于三层网络结构，提出RTD可编程逻辑门的函数综合算法，且文献[17]算法较文献[9]算法的效率更高、设计的电路更简单，但仍存在不足。本文将基于新的定理，提出一种n变量函数实现算法，能有效解决文献[17]算法的不足，且算法准确性更高、设计的电路更简单。

1 相关理论及RTD可编程逻辑门

1.1 相关理论

1.2 RTD可编程逻辑门

基于RTD的阈值电路结构通常由MOBILE和输入分支组成[11-12]。MOBILE可由2个RTD串联得到，电路图如图1所示。在图1中，位于上方的RTD为负载管，位于下方的RTD为驱动管，Vclk为时钟电压[19]，y为输出端。由于当RTD的电流密度一定时，RTD的波峰电流与其面积成正比，且波峰电流较小的RTD先进入负阻区，呈现的阻抗较大，故电路的输出y取决于负载管和驱动管的面积[6]。当负载管的面积比驱动管的面积小时，y输出低电平；反之，y输出高电平。当MOBILE加入输入分支时，便可实现阈值电路。输入分支由RTD和HFET的串联结构组成[20]。当输入分支与负载管并联时，称为正输入分支；当输入分支与驱动管并联时，称为负输入分支。RTD可编程逻辑门电路如图2所示，其中A表示RTD的单位面积，c1～c2n表示输入端信号。该RTD由n个正输入分支、n个负输入分支和MOBILE组成，称其为n输入RTD可编程逻辑门[21]，其输入输出关系可表示为

图1 MOBILE电路图Fig.1 The circuit of MOBILE

图2 RTD可编程逻辑门及其电路符号Fig.2 RTD programmable logic gate and its circuit symbols

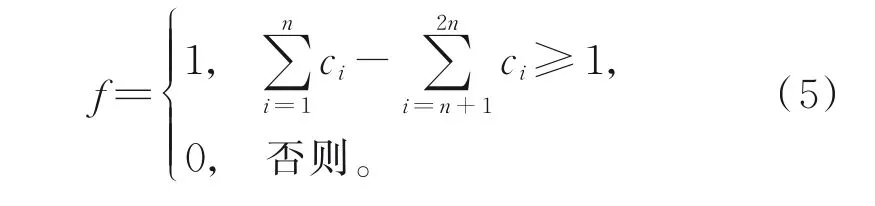
采用如图2所示的RTD可编程逻辑门可实现任意n变量函数[9]。同时采用定理1和定理2方法，可提高算法的准确性，且电路更简单。

2 n变量函数的实现

二进制神经网络的结构分为输入层、隐层和输出层3层[16，21]。其中，输入层的作用是对输入信号进行整形，以保证输入信号时序一致；隐层是网络的核心，实现所需的逻辑功能；输出层用于处理隐层结果，以得到正确的输出。目前，已有不少实现逻辑函数的3层网络结构算法[14-15]，但得到的逻辑函数其阈值和权值的取值范围过大，不利于电路设计。

由于利用一个n输入RTD可编程逻辑门能实现符合定理1的任意n变量函数[9]，可在隐层中对输入向量的真假性进行变换，并在输出层中进行纠错处理。文献[9]采用定理1提出的隐层及输出层算法，虽然可实现任意n变量函数，且能用RTD可编程逻辑门设计电路，但效率较低，设计的电路也较复杂。文献[17]对文献[9]的算法进行了改进，使设计的电路较简单，但算法尚存在以下不足：

（1）由于假向量对隐层函数的权重无影响，若将输入向量真假性变换次数均加1，可能导致算法出错。

（2）在被覆盖的所有真向量中，未考虑真假性变换次数的奇偶性。

本文提出的n变量函数实现算法，能较好地解决文献[17]算法的不足，且准确性更高，设计的电路更简单。

2.1 基本概念与记号

算法基本框架：在隐层中，产生隐层函数，实现所需的逻辑功能；在输出层中，产生输出层函数，调整隐层的结果，得到正确的输出[21]。隐层函数的产生是算法的关键，可采用定理1及定理2方法实现，但需将某些假向量临时看作真向量，其核心向量可为真向量，也可为假向量。产生隐层函数后，被覆盖的向量需根据真假性变换情况对其复原。

按照汉明距离从大到小搜索所有输入向量。当汉明距离不为1和0，且满足可产生隐层函数的条件时，采用定理1方法产生隐层函数；当汉明距离为1，且满足可产生隐层函数的条件时，采用定理2方法产生隐层函数。由于定理2中的阈值函数出现了权值为±2的项，为防止RTD可编程逻辑门中出现较多无实际作用的输入端，需判断该隐层函数能否使用n+1输入的RTD可编程逻辑门。

算法中的记号如下：

chi表示输入向量Xi的变换次数；

d表示汉明距离；

si表示将输入向量Xi当作核心向量进行覆盖时，被覆盖的向量中chi为正的向量数；

ti表示将输入向量Xi当作核心向量进行覆盖时，被覆盖的向量中chi为负的向量数；

li表示将输入向量Xi当作核心向量进行覆盖时，被覆盖的向量数；

g表示隐层函数；

k表示某隐层函数在输出层中的权重，简称为隐层函数权重；

f表示输出层函数；

best_vector 1表示最优输入向量，且用该最优向量判断其能否作为定理1中的核心向量；

best_vector 2表示最优输入向量，且用该最优向量判断其能否作为定理2中的核心向量。

2.2 变换次数、最优输入向量与隐层函数权重

首先，对所有真向量的chi标记为+1，对所有假向量的chi标记为0。在采用定理1方法产生隐层函数时，若该隐层函数的权重为+1，则对所有被其覆盖的向量的chi－1；若该隐层函数权重为 －1，则对所有被其覆盖的向量的chi+1。当采用定理2方法产生隐层函数时，若该隐层函数的权重为+1，则对所有被其覆盖的真向量（不包括核心向量）及核心向量（不管真假）的chi－1；若该隐层函数的权重为－1，则对所有被其覆盖的真向量（不包括核心向量）及核心向量（不管真假）的chi+1。

输入向量的真假性可由chi确定：若chi为0，则为假向量；若chi非0，则为真向量。

当以某个汉明距离搜索所有向量时，由于可能需同时判断多个输入向量能否作为核心向量，因此需选择其中最优的输入向量。在判断能否作为定理1中的核心向量时，选择其中被覆盖的假向量最多的为最优输入向量。如果仍存在多个，则选择chi绝对值最小的为最优输入向量，记为best_vector 1。在判断能否作为定理2中的核心向量时，选择其中被覆盖的假向量最多的为最优输入向量。如果仍存在多个，则选择ωi最小、且chi不为0的为最优输入向量；若chi均为0，则选择ωi最小的为最优输入向量，记为best_vector 2。其中，

在被覆盖的向量中，若chi为正的向量比为负的多，则隐层函数权重+1；若chi为负的向量比为正的多，则隐层函数权重－1；若chi为正的向量与为负的一样多，则对这些向量的chi求和，若求和后的值为负，则隐层函数权重－1，若求和后的值为正或0，则隐层函数权重+1。

2.3 算法实现步骤

3 算法检验与比较

例 1若四变量函数f(x1，x2，x3，x4)的卡诺图如图3所示，试通过算法实现该四变量函数。

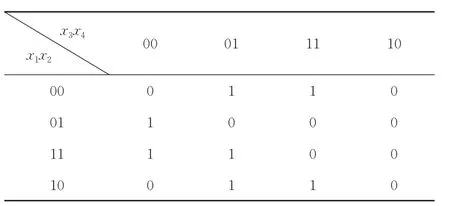
图3 四变量函数 f(x1，x2，x3，x4)的卡诺图Fig.3 Karnaugh map of four-variable function

将所有输入向量Xi中真向量的chi设为+1，假向量的chi设为0。由于变量数大于2，先执行步骤（3）～步骤（8）的循环。以d1=[(n+1)/2]=2作为汉明距离，将每个输入向量Xi依次作为核心向量，得到的|max{si，ti}|为6。该值对应的输入向量有X1，X5，X8，X9和X13，可选X5或X8作为 best_vector 1。将X5作为核心向量，由于|2max{s5，t5}|=12＞l5=11，因此采用定理1方法产生隐层函数g1，隐层函数权重为k1=+1。更改向量的 chi：向量X0，X5，X6，X7和X15的 chi减 1 后变为－1，向量X1，X3，X4，X9，X12和X13的chi减1后变为0。同理，此时d2=[(n+1)/2]=2，可 得 到 最 优 向 量X9，X10或X12。 由 于|2max{s9，t9}|=10＜l9=11，故以 1作为汉明距离，将每个输入向量Xi依次作为核心向量，得到|max{si，ti}|=4。该值对应的输入向量为X7，并将X7作为 best_vector 2。由于|max{s7，t7}|＞1，因此执行步骤（13）～步骤（20）的循环。以X7作为核心向量，用定理2方法产生函数y。由于函数y可用（4+1）输入的RTD可编程逻辑门实现，故可产生隐层函数g2，隐层函数权重k2=-1。更改向量的chi：向量X5，X6，X7和X15的 chi加 1 后变为 0，此时，|max{si，ti}|=1，执行步骤（22），可得到隐层函数g3，g4及隐层函数权重k3=-1，k4=+1。

得到的隐层函数为：

输出层函数为

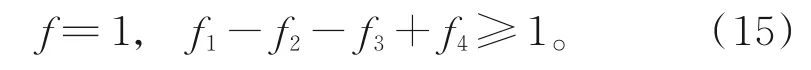
采用本文算法得到的隐层函数和输出层函数电路如图4所示。在图4中，隐层函数g1，g2，g3和g4的电路用时钟信号Vclk1实现，输出层函数f的电路用时钟信号Vclk2实现。当时钟信号Vclk1处于上升沿时，电路输出隐层函数g1，g2，g3和g4的结果；当时钟信号Vclk2处于上升沿时，电路输出输出层函数f的结果。对图4所示的电路进行HSPICE仿真，结果如图5所示。可知，用本文算法设计的电路输出结果正确，该电路共用了5个RTD可编程逻辑门，其中，2个为三输入RTD可编程逻辑门、1个为二输入RTD可编程逻辑门、2个为四输入RTD可编程逻辑门。而文献[17]算法在汉明距离为1时，由于存在多个可选的输入向量，若选择不同的输入向量作为核心向量，则得到不同的结果，且设计的最优电路需要6个RTD可编程逻辑门，其中，5个为三输入RTD可编程逻辑门、1个为四输入RTD可编程逻辑门。采用本文算法得到的电路较文献[17]方法少用了1个RTD可编程逻辑门，电路更简单。

图4 四变量函数实现电路Fig.4 Realization circuit of four-variable function

图5 四变量函数实现电路的HSPICE仿真Fig.5 HSPICE simulation of realization circuit of four-variable function

例 2若五变量函数f(x1，x2，x3，x4，x5)的卡诺图如图6所示，试通过算法实现该五变量函数。

图6 五变量函数 f(x1，x2，x3，x4，x5)的卡诺图Fig.6 Karnaugh map of five-variable function

将所有输入向量Xi中真向量的chi设为 +1，假向量的chi设为0，d1=[(n+1)/2]=3。执行步骤（4）和步骤（5），可找到 best_vector 1为X18。由于|2max{s18，t18}|=34＞l8=26，可产生隐层函数g1，隐层函数权重k1=+1。更改相应向量的chi后，由于max{si，ti}=9，d2=d2-1=2，再执行步骤（4），可找到 best_vector 1为X18。由于|2max{s18，t18}|=14＜l18=16，d2=d2-1=1。执行步骤（11）和步骤（12），可得|max{si，ti}|=4，对应的输入向量为X16和X19；由于ω19=1＜ω16=3，故选择X19作 为best_vector 2。再执行步骤（14）～步骤（16），可得隐层函数g2，隐层函数权重k2=-1。更改相应向量的 chi后 ，再执行步骤（17）和步骤（18），可得best_vector 2 为X20。由于|max{s20，t20}|=3，执行步骤（14）～步骤（16），可得隐层函数g3，隐层函数权重k3=-1。更改相应向量的 chi，此时，|max{si，ti}|=1，执行步骤（22），可得隐层函数g4，g5和g6，隐层函数权重k4=-1，k5=-1，k6=+1。

得到的隐层函数为：

输出层函数为

由隐层函数和输出层函数设计的电路如图7所示。在图7中，利用时钟信号Vclk1实现隐层函数g1，g2，g3，g4，g5和g6，利用时钟信号Vclk2实现输出层函数f。当时钟信号Vclk1处于上升沿时，输出隐层函数g1，g2，g3，g4，g5和g6的结果；当时钟信号Vclk2处于上升沿时，输出输出层函数f的结果。对图7所示电路进行HSPICE仿真，其结果如图8所示。可知，采用本文算法设计的电路具有正确的输出结果，用7个RTD可编程逻辑门即可实现，即1个六输入RTD可编程逻辑门、4个四输入RTD可编程逻辑门和2个五输入RTD可编程逻辑门；采用文献[17]算法设计的最优电路需要11个RTD可编程逻辑门：1个五输入RTD可编程逻辑门和10个四输入RTD可编程逻辑门[21]。采用本文算法设计的电路较文献[17]算法少用了4个RTD可编程逻辑门，电路更简单。

图7 五变量函数实现电路Fig.7 Realization circuit of five-variable function

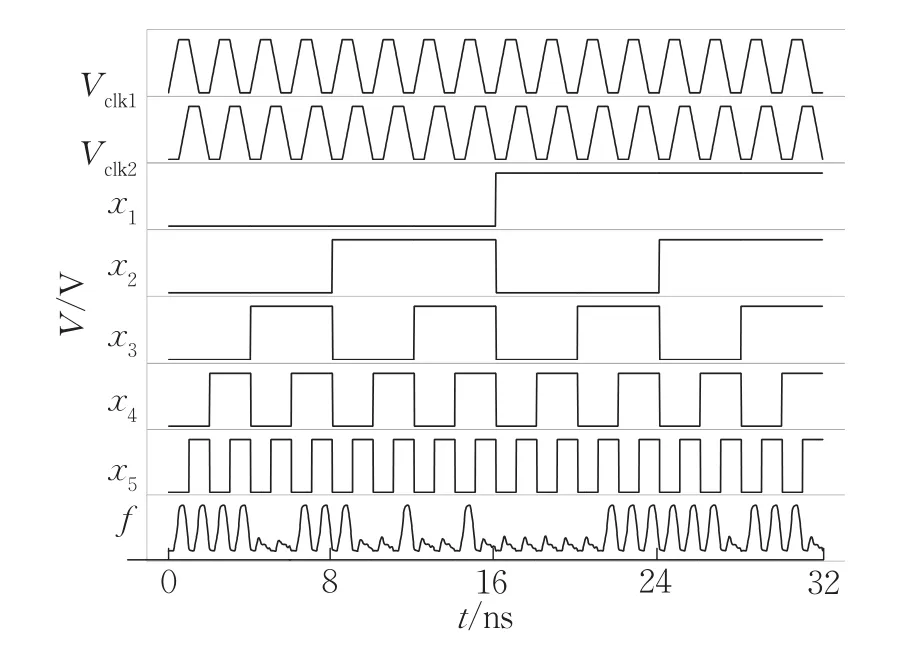
图8 五变量函数实现电路的HSPICE仿真Fig.8 HSPICE simulation of realization circuit of five-variable function

4 总 结

基于二进制神经元模型中的三层网络结构及相关定理，提出了基于RTD可编程逻辑门的n变量函数实现算法，很好地解决了文献[17]算法的不足，且准确性更高，设计的电路也更简单，特别是当变量数较多时，优势更明显。