Estimation Based Adaptive Constraint Control for a Class of Coupled String Systems
Sai Zhang, Li Tang,, and Yan-Jun Liu,
Dear editor,
In this letter, the boundary tension constraint-based adaptive boundary control problem is investigated for a class of flexible string systems with unknown boundary disturbances and unknown parameters, with the purpose of suppressing transverse and longitudinal vibrations. Firstly, on the basis of the Hamiltonian principle, two partial differential equations for a transverse-longitudinal coupled string with spatiotemporally varying tension are derived. Secondly,the transverse and longitudinal adaptive boundary controllers are designed by constructing Lyapunov functions. A barrier Lyapunov function is adopted to confine the boundary tension within the constraint and disturbance observers are designed to estimate the unknown boundary disturbances. Finally, stability analysis of the closed-loop system is performed. The simulation results further illustrate the effectiveness of the proposed method.
String structures are widely existed in modern industry, such as telephone lines, cableways, transmission belts, crane suspensions,crane cables for subsea installations [1]. However, in practical applications, string systems are subject to external environmental disturbances such as aerodynamic forces, wind or currents, which cause the vibration of systems [2], [3]. Undesirable vibrations degrade system performance, reduce efficiency, and even create premature fatigue problems [4]. In addition, the actual tension on the string is often not a constant from the internal structural analysis and it varies with the vibration displacement and time [5]. Excessive tension on the string structure causes it to develop large vibrations[6]. Consequently, during production work, the tension value needs to be constrained to a restricted space to avoid serious hazards. At the same time, effective control mechanisms need to be utilized to reduce string vibrations, thereby improving the operational performance of the system.
The string system can be described by partial differential equations(PDEs). PDE systems possess infinite dimensional properties, which makes system dynamics difficult to control [7]. Recently, boundary control has been regarded by many scholars as an economical and easy-to-implement approach for controlling infinite dimensional systems [8]. It requires only actuators and sensors at the boundary of system and does not affect the dynamics model of system [9]. Given these advantages, boundary control has been applied in many research areas [10], [11]. In addition, adaptive control approach is an effective method to deal with parameter uncertainty [12], which can actively respond to the dynamic characteristics of system, thus improving the control. Researchers have done a lot of research work on this topic [13]−[15]. Heet al. [16] considered the transverse and longitudinal displacements of string system. Krstic and Smyshlyaev[17] studied the adaptive control problem of parabolic PDEs based on the PDE-backstepping method. In spite of the great progress that has been made in adaptive boundary control, there are still some challenging difficulties. In practical engineering, since physical constraints, environ- mental limitations and safety needs, certain states in the system are usually subject to certain restrictions.
The barrier Lyapunov function (BLF) is an efficient method to tackle the constraint problem [18]. Therefore, more and more scholars are using BLF to address the constrained control problems of nonlinear systems [19], [20]. He and Ge [21] proposed a cooperative control strategy for a portal crane system with tension constraint. A study on vibration suppression of the flexible riser with top tension constraint was presented in [22]. However, the research results on the control of string systems with the boundary tension constraint are limited. In practical engineering, excessive tension increases the wear of string with respect to the tip load. Therefore, it is essential and meaningful to study the boundary tension constraint issue to suppress the vibration of the string system.

Control objective: The control objective is to deal with the coupling effect between transverse and longitudinal displacements under time-varying disturbances by designing transverse and longitudinal controllers at the boundary of the string such that: 1) The boundary tension on the string does not violate the constraint; 2) The transverse and longitudinal vibrations of the string are effectively suppressed and remain near the equilibrium position under timevarying disturbances; 3) The closed-loop system is stable and all signals are bounded.



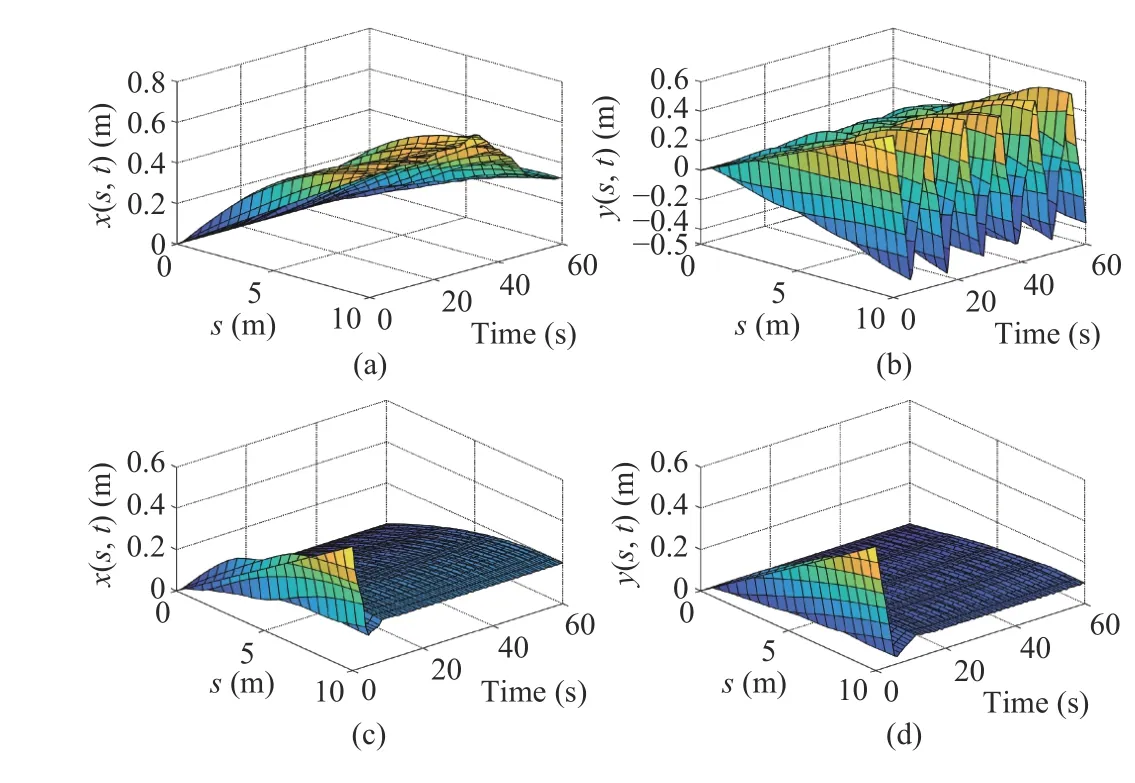
Fig. 1. The displacement of the string. (a) x(s,t) without control; (b)y(s,t)without control; (c) x(s,t) with the adaptive boundary control; (d) y (s,t) with the adaptive boundary control.

Fig. 2. Adaptive controllers applied to the coupled string system. (a) Thetrajectory of xs(ℓ,t) ; (b) The trajectory of the boundary tension T (ℓ,t).

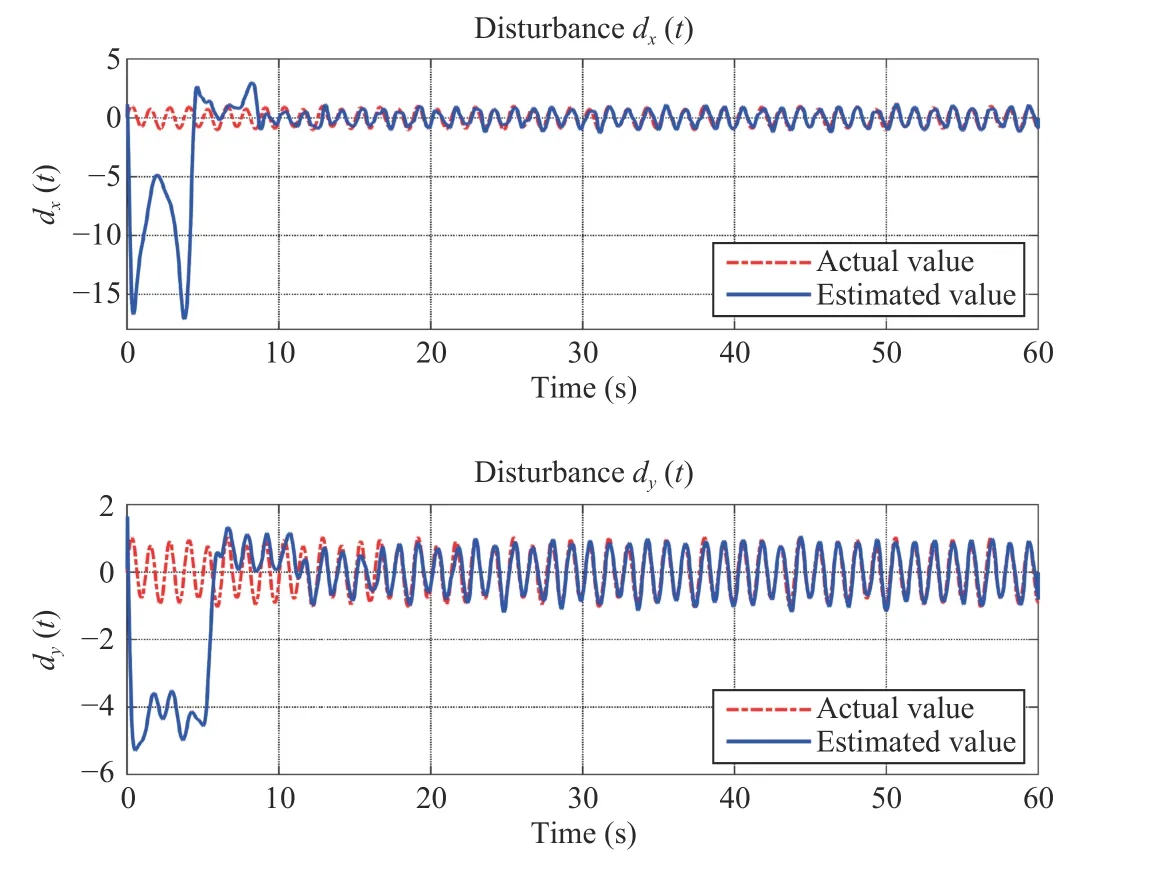
Fig. 3. Disturbance dx(t) and dy(t) tracking: Actual value (dotted line) and estimated value (solid line).

Fig. 4. The trajectory of control inputs.

Acknowledgments: This work was supported in part by the National Natural Science Foundation of China (61973147,61903168, 62025303), and the Liaoning Revitalization Talents Program (XLYC2007177), the Doctoral Research Initiation of Foundation of Liaoning Province (2020-BS-243).
 IEEE/CAA Journal of Automatica Sinica2022年8期
IEEE/CAA Journal of Automatica Sinica2022年8期
- IEEE/CAA Journal of Automatica Sinica的其它文章
- Consensus Control of Multi-Agent Systems Using Fault-Estimation-in-the-Loop:Dynamic Event-Triggered Case
- A PD-Type State-Dependent Riccati Equation With Iterative Learning Augmentation for Mechanical Systems
- Finite-Time Stabilization of Linear Systems With Input Constraints by Event-Triggered Control
- Exploring the Effectiveness of Gesture Interaction in Driver Assistance Systems via Virtual Reality
- Domain Adaptive Semantic Segmentation via Entropy-Ranking and Uncertain Learning-Based Self-Training
- Position Encoding Based Convolutional Neural Networks for Machine Remaining Useful Life Prediction
