利用拉格朗日中值定理对可微函数进行积分估计
李容星 (湖北师范大学文理学院,湖北 黄石 435109)
一、引 言
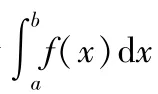
对于多次连续可微的函数而言,如果能满足类似的条件,则可以利用泰勒定理进行积分估计并得到类似的结果.
二、积分中值定理
我们首先引入拉格朗日中值定理:
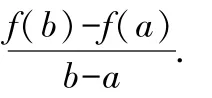
拉格朗日中值定理有如下积分中值定理:
设函数()在[,]上连续,则存在∈(,)使得

即定理1 得证.
设函数(),()在[,]上连续,且()在[,]上不变号,则存在∈(,)使得
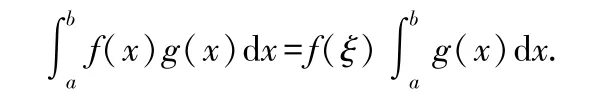
不妨设在[,]上()≥0,于是()≤()()≤(),其中,分别是()在[,]上的最大值和最小值.积分有
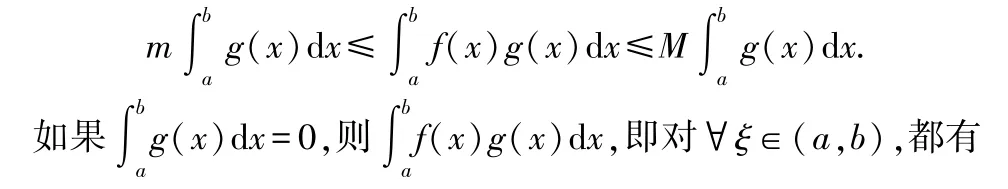
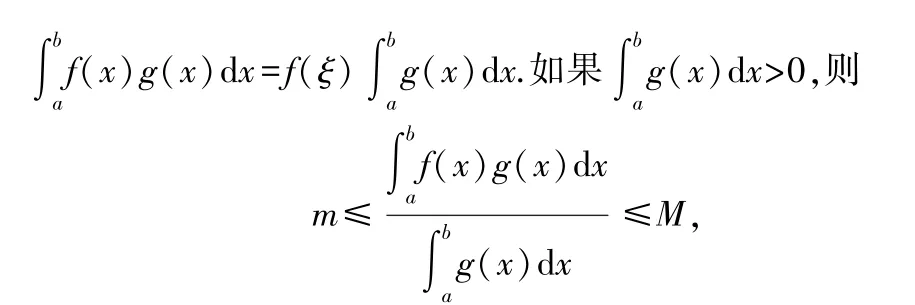
由介值定理,存在∈(,)使得
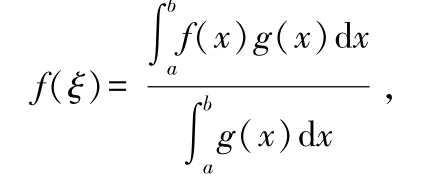
即定理2 得证.
三、可微函数的积分估计
如果函数()在(,)内存在一点为0,则可以利用拉格朗日中值定理得到如下结论:

说明:(1)观察证明可知,其取等的充要条件为在该区间上有()≡,即()为一个一次函数;
手术很成功,癌细胞被切除了。郑全意浑身的细胞又全部投入工作状态。事实上,此前处在所谓“保守治疗”之中的他,就用“发自肺腑”的声音、用手写指令的办法,办理了北京市第一起食品涉刑案件—肉皮冻非法添加双氧水案。出院之后,他又带领团队成功查处了毒豆芽事件、馒头房非法添加案等一系列案件,努力扫除昌平父老餐桌上的种种“癌细胞”。
(2)如果函数()的零点不是在[,]的中点处,而是在其他位置,则可以利用类似定理3 中的证明,得到类似的结论.
当函数在区间端点处等于0 时,可以得到同样的结论:
设函数()在[,]上连续可导,且()=()=0,则


利用泰勒定理则可以得到如下结论:

即定理5 得证.
说明:(1)如果函数()的零点不是在[,]的中点处,而是在其他位置,则可以利用类似定理5 中的证明,得到类似的结论;
(2)如果函数()的一阶导数本身是有界的,则可以进行一些更强的估计.
当函数在区间端点处等于0 时,可以得到类似的结论:
设函数()在[,]上两次连续可微,且()=()=0,则
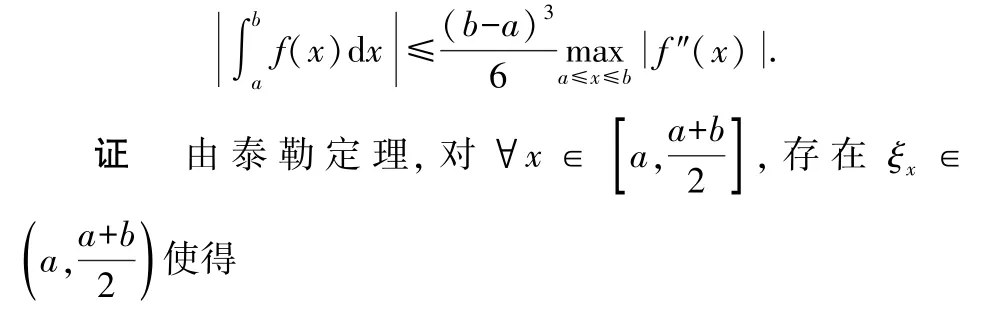

说明:定理3 和定理4 的结论相同,而定理5 和定理6 的结论是不同的.
上述定理5 和定理6 也可以推广到高阶导数的情形:
设函数()在[,]上2次连续可微,且
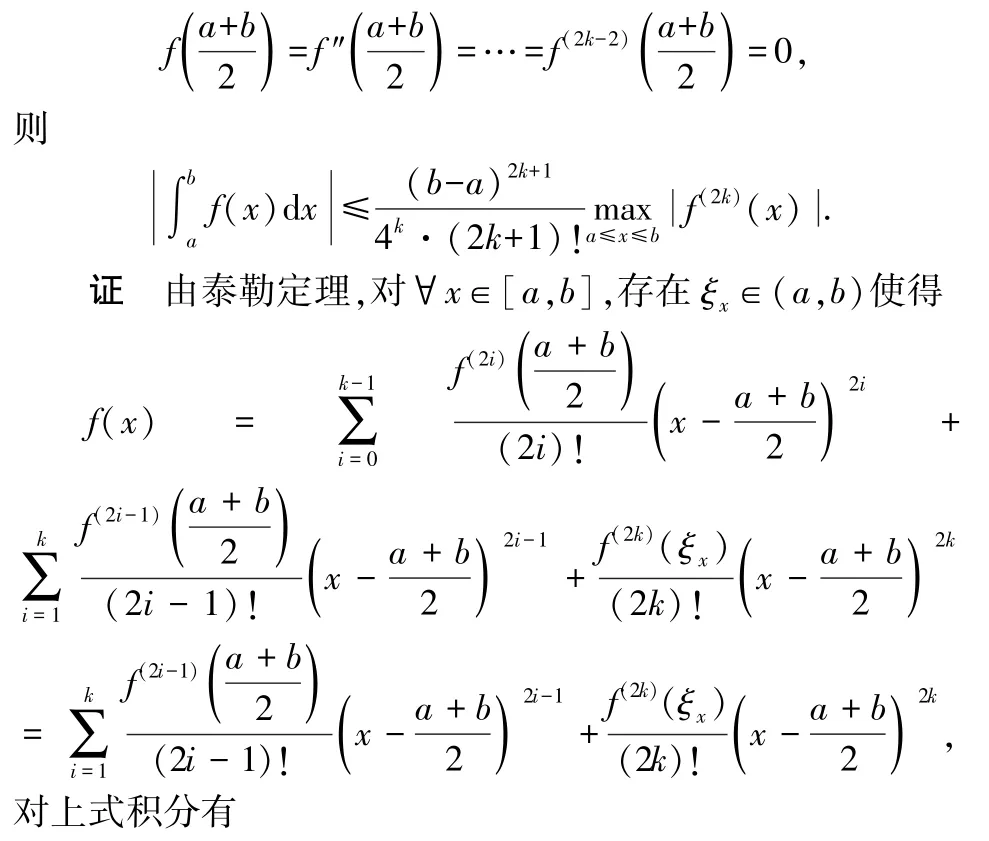

四、在高等数学中的应用
2009 年全国大学生数学竞赛非数学类初赛设函数在01上二阶连续可微过点00与点11的直线与曲线=相交于点其中0<<1.求证存在∈01使得=0.

由积分的恒等性可知()≡|-1 |.但|-1 |在=1 处不可导,矛盾,故这样的函数不存在.


五、结 语
利用函数的性质对函数的积分进行估计是数学分析中一个非常重要的工作.本文首先利用拉格朗日中值定理对一次连续可微的函数进行估计,然后利用泰勒定理对多次连续可微的函数进行估计,最后把相关的思想运用在高等数学中.该思想的本质是利用拉格朗日定理或者泰勒定理结合函数本身导数的性质对函数进行估计,只要掌握好该思想,就能够简化高等数学中相关问题的推导.我们也在具体教学的过程中进行了推广,这不仅有利于学生对拉格朗日定理或者泰勒定理的学习,也能够激发他们学习的兴趣.

