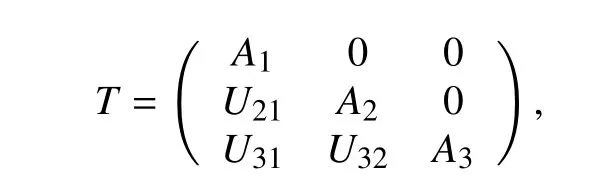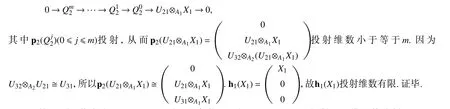3 阶三角矩阵环上的Gorenstein 投射模及其维数
杨 瑞,王 淼,王占平
(西北师范大学 数学与统计学院,甘肃 兰州 730070)
1969 年,Auslander 等[1]研究了双边Noether 环是上G-维数为0 的有限生成模.1993—1995 年,Enochs等[2-3]定义了任意环R上 的Gorenstein 投射模、Gorenstein 内射模和Gorenstein 平坦模.2009 年,陈小松等[4]研究了Neother 整环上的复合Groebner 基.设A,B是环,U是 (B,A)-双模,是2 阶三角矩阵环.当T是Artin 代数时,2012—2013 年,Xiong 等[5-6]讨论了在什么条件下T是Gorenstein 代数,并对Gorenstein 投射左T-模进行了研究.2014 年,Enoches 等[7]引入了Gorenstein 正则环,并在这个环上给出了左T-模是Gorenstein 投射(内射)模的充要条件.2011 年,Enoches 等[8]对n阶三角矩阵环的同调性质进行了研究.2015 年,朱荣民等[9]在Gorenstein 正则环的条件下,研究了n阶三角矩阵环的Gorenstein 投射模及其维数.2016,朱荣民等[10]进一步研究了三角矩阵环T上模的Gorenstein 同调维数.2020 年,Li 等[11]在较弱条件下,给出了T-模是Gorenstein 投射模的充要条件.
受文献[9]结论的启发,本文主要研究3 阶三角矩阵环上的Gorenstein 投射模及其维数.在较弱条件下,得到了一个模是3 阶三角矩阵环上的Gorenstein 投射模的等价刻画,并研究了3 阶三角矩阵环上模的Gorenstein 投射维数.
本文提到的环均指有单位元的结合环,模指酉模.设R是环,我们用R-Mod(Mod-R)表示左(右)R-模范畴,P(R)表示所有投射左R-模构成的类.pdRM,idRM,GpdRM和fdMR分别表示左R-模M的投射维数、内射维数、Gorenstein 投射维数和右R-模M的平坦维数.
根据文献[8]定义1.1,设Ai(i=1,2,3)均是环,对每个1≤j T按矩阵的加法和乘法做成环,称为3 阶三角矩阵环. 设T是3 阶三角矩阵环.我们总假设U32⊗A2U21≅U31. 首先回顾Gorenstein 投射模的定义. 定义 1[12]称左R-模M是Gorenstein 投射模,如果存在投射左R-模的正合列 定义 2[12]设M是左R-模.M的Gorenstein 投射维数GpdRM=inf{n∈N|存在R-模正合列0 →Gn→···→G1→G0→M→0,其中Gi是Gorenstein 投射R-模,i=1,2,···,n}.若这样的n不存在,则令GpdRM=∞. 定义 3[13]设···是M的投射分解.令K0=M,Ki=cokerdi+1,i=1,2,···.称Ki是M的第i个合冲. 下面给出几个引理,主要用于刻画3 阶三角矩阵环上的Gorenstein 投射模. 引理 1[11]对任意环R,以下成立: (1) 设 X•是正合序列,每个Xi∈P(R),M∈R−Mod.若idRM<∞,则HomR(X•,M)正合.设 X•是完全投射分解.若pdRM<∞,则HomR(X•,M)正合. (2) 设 X•是正合序列,每个Xi∈P(R),M∈R−Mod.若fdMR<∞,则M⊗RX•正合. 显然,函子 pi保持投射对象.在文献[9]中,作者证明了:在左Gorenstein 环上,函子 pi保持Gorenstein 投射对象.下面我们在更弱的条件下,即一般环上,得到了3 阶三角矩阵环上的类似结论. 命题 1设T是3 阶三角矩阵环.Uij(1 ≤j 因为pdU21<∞,所以U21⊗A1X1同构于U21的拷贝直和的直和项,于是U21⊗A1X1投射维数有限.设pd(U21⊗A1X1)=m,则有左A2-模的正合列 文献[9]中,作者在Gorenstein 正则环的条件下,给出了Gorenstein 投射左T-模的等价刻画,以及Gorenstein 投射维数的刻画.下面我们在较弱的条件下,即一般环上,给出3 阶三角矩阵环上类似的刻画. 每个复形Fj⊗Aiqi(P•)(0 ≤j≤m)零调,由文献[13]定理6.3 得Uki⊗Aiqi(P•)零调.考虑交换图 证明(1)⇒(2)因为GpdM≤m,所以有正合列