等离子体中双流体模型的调制逼近*

刘慧敏，蒲学科

（1.山西财经大学 应用数学学院，太原 030006；2.广州大学 数学与信息科学学院，广州 510006）

引 言

等离子体模型是指在研究复杂的非平衡态等离子体时，经常遇到多参变量的情况，为了从理论上定量地或定性地描述它们，利用一些互相补充的简化模型常常是很有益的[1-2].本文在一维直线上考虑下列等离子体中的简化双流体模型：

其中n表示离子的密度，v表示离子的速度，E 表示高频电场，ϕ是低频电场的势函数，这些函数均定义在(x,t)∈R×R+上.此模型描述了离子声波与等离子体波的相互作用，来源于Euler-Maxwell 系统，即由离子和电子的Euler 方程，以及电场和磁场的Maxwell 方程耦合的双流体模型.模型(1)的推导过程可参考文献[3]及其相关文献.

对于双流体模型(1)，Guo 和Huang[4]利用常微分方程方法证明了孤立波的存在性、唯一性以及无穷远处的渐近行为.Han、Zhang 和Guo[5]证明了三维空间中平衡态附近扰动解的整体存在性，该结果推广了Guo 和Pausader[6]关于离子Euler-Poisson 模型(2)在三维空间中的小振幅整体光滑无旋解.事实上，当忽略高频电场效应时，双流体模型(1)退化为下列离子Euler-Poisson 模型：

对于离子Euler-Poisson 模型(2)，Guo 和Pu[7]首次严格建立了一维冷离子以及热离子两种情形的KdV 极限.Pu[8]对高维的情形，即二维的KP-II 极限以及三维的ZK 极限进行了研究.之后，Liu 和Pu[9]严格证明了带量子效应的退化双流体模型的量子KdV 极限.由于KdV 方程的解恰是非线性Schrödinger (NLS)方程在小波数区域的解，故考虑色散模型的NLS 逼近是很有意义的事情.作为著名的非线性逼近方程，NLS 方程在一维直线上是完全可积的Hamilton 系统，可以借助反散射方法对其求解[10].1968年，Zakharov[11]从流体动力学方程推导出了NLS 方程，用于考虑具有无限深度的自由表面理想流体.随着研究的深入，学者们发现了一些重要的非线性波动现象（如等离子体中的离子声波、电场中超导电子的运动以及非线性光学的自陷现象等）都可以用NLS 方程进行描述[12-13].最近，Liu 和Pu[14]利用normal-form 变换以及修正能量的方法严格证明了离子Euler-Poisson 模型(2)的NLS 逼近.本文将此结果[14]推广到双流体模型(1)的调制逼近.双流体模型(1)是一个高度耦合的双曲方程组，其线性色散关系有两个：

因而在研究调制逼近过程中，需要寻找合适的满足耦合方程组兼容性的形式逼近解.本文考虑下列基本空间波数k0=0的关于时间震荡的形式波列解：

其中 0＜ϵ ≪1是一个小扰动参数，A表示复值振幅，c.c.表示复共轭.将式(4)代入模型(1)中，可得复振幅A满足下列NLS 方程：

其中X=ϵx∈R，T=ϵ2t∈R，即时间和空间的调制尺度分别为O (1/ϵ2)和 O (1/ϵ)，系数满足νj∈R,j∈{1,2}.

严格证明上面阐述的NLS 逼近过程不是一件容易的事情.Kalyakin[15]首次真正意义上地证明了拟线性色散系统的NLS 逼近结果，然而该系统中拟线性二次项被完全排除在外.目前，带有拟线性二次项色散系统的NLS 逼近已取得了部分重要结果.具体来说，可以针对系统本身特点，寻找特殊变换将二次项消除，例如忽略表面张力且考虑无限深度的二维和三维水波问题[16-17].再如拟线性KdV 方程，Schneider[18]利用Miura 变换得到了NLS 逼近结果.另外，当原系统中右端二次项只丢失1 /2阶导数时，可以借助normal-form 变换消除二次项，如忽略表面张力且考虑有限深度的二维水波问题.此时，由于变换后系统的右端项会丢失一阶导数，从而通过Cauchy-Kowalevskaya 定理便可得到NLS 逼近结果[19-20].利用normal-form 变换消除双曲系统中半线性二次项的方法最早在文献[21]中被介绍.Kalyakin[15]首次利用normal-form 变换证明了NLS 逼近理论.另外，当二次项丢失一阶导数时，可以利用normal-form 变换修正能量泛函的方法，有效处理由拟线性项丢失导数引起的困难，例如Düll[22]证明了拟线性Klein-Gordon 方程在Sobolev 空间中的NLS 逼近结果，注意到这里的拟线性Klein-Gordon 方程的线性色散关系不会引起共振点.此外，Liu 和Pu[14]得到了离子Euler-Poisson 方程组的NLS 逼近结果，与上述模型不同，离子Euler-Poisson 方程组不仅二次项丢失一阶导数，而且会出现非平凡共振点，他们在Fourier 空间中利用截断函数修正误差，并通过投影算子将误差的高低频部分分开，对低频部分直接应用normal-form 变换，对高频部分则利用此变换定义新的能量泛函，从而解决了由导数丢失以及共振点出现带来的双重困难.最近，Bian、Liu 和Pu[23]严格证明了一维带量子效应的退化双流体模型的NLS 逼近结果，其中量子项会引起更高阶导数的出现.另外，Düll[24]在弧长坐标下严格证明了二维有限深度水波的NLS 逼近，其中带表面张力和不带表面张力的情形均包含在内.注意到本文考虑的双流体模型(1)是一个高度耦合的色散模型，包含两种完全不同的色散关系，既会出现共振点又会损失导数，因而与上述列举模型均有所不同.本文将利用normal-form 变换消除低阶项，结合方程本身的特点去构造合适的修正能量泛函，最终严格论证双流体模型(1)的NLS 逼近结果.

定理1固定sA≥6，对于所有的C1,T0＞0，都存在常数C2＞0,ϵ0＞0，使得当NLS 方程(5)的所有解A∈C([0,T0],HsA(R,C))满足

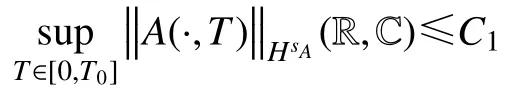
时，下面的陈述成立.对于任意的ϵ ∈(0,ϵ0)，模型(1)的解存在

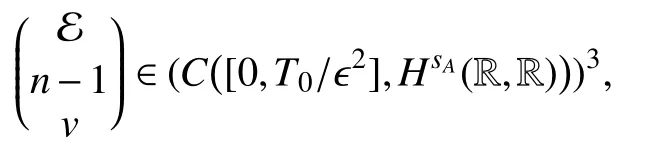
且满足

注1对于任意的t∈[0,T0/ϵ2]，相对于真实解 (E,n-1,v)和 逼近解 (ϵAeit+c.c.,ϵ2|A|2ζ)来 说，定理1 中阶为O(ϵ3/2)和O(ϵ5/2)的误差是足够小的.换言之，由于NLS 逼近存在的时间尺度 ϵ-2足够长，从而保证在原系统模型(1)中能够很好地观察到NLS 方程的动力学行为.

注2定理1 中误差的光滑性与复振幅A的光滑性一致，这一点可以通过修正逼近解使其在Fourier 空间中有紧支集来实现，这是因为逼近解在Fourier 空间中的支集集中在k=0的某个邻域.具体细节可参见本文第3 节.

注3由于双流体模型(1) 中出现了拟线性二次项，这会引起三方面困难.首先，为了在时间尺度 O(ϵ-2)上严格证明NLS 逼近，需要利用normal-form 变换消去误差方程中阶为O (1)的非线性项，而双流体模型(1)的色散关系(3)导致消去过程中出现共振点k=0，本文充分利用了拟线性二次项在k=0处消失的特点来处理共振点.其次，拟线性二次项会损失一阶导数，因此在对误差进行一致能量估计的过程中，需要充分利用模型的结构特点解决导数损失的问题.最后，双流体模型(1)的高度耦合性以及两种完全不同的色散关系，使得在克服前两种困难时需要更加细致的分析.

本文具体结构如下：第1 节列出本文中需要用到的记号以及预备引理；第2 节从形式上将NLS 方程导出，并给出余项的估计；第3 节利用normal-form 变换消去误差方程中的低阶项；第4 节充分利用误差方程结构，通过构造合适的修正能量泛函得到误差的一致能量估计，从而严格证明了本文主要结论.

1 预备知识

符号说明函数u∈L2(R,K)的Fourier 变换定义如下：

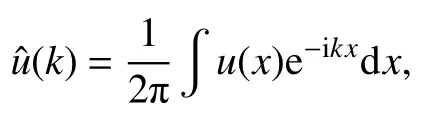
其中K=R或者K=C.Hs(R,K)表示从R映到K的函数空间.u∈Hs(R,K) 意着存在常数C使得

‖u‖Hs(R,K)≤C.

泛函空间Lp(m)的定义如下：

u∈Lp(m)(R,K)⇔uϱm∈Lp(R,K),

引理1(Cauchy-Schwarz 不等式) 设f,g在 R 上可积，则

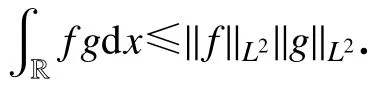
引理2(Young 不等式) 设a,b是非负实数，p＞1,那么

j∈{±1}aj∈H2(R,R)fj∈H1(R,R)

引理3设，且，则有

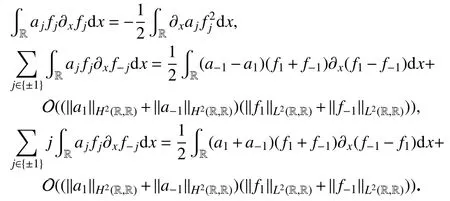
引理3的证明可以参考文献[10]中的引理5.3.

引理4(交换子估计)[25]设m≥1是一个整数，定义交换子如下：

则该交换子有下列估计：

其中p,p2,p3∈(1,∞)，且有

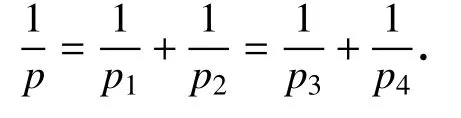
2 形式推导和余项估计

为了从双流体模型(1)中形式推导出NLS 方程，首先将式(1)写成一阶偏微分方程组.为此，取平衡解附近的扰动解ρ=n-1，则由模型(1)中的Poisson 方程可知，存在可逆算子(ρ,E)→φ(ρ,E)，使得

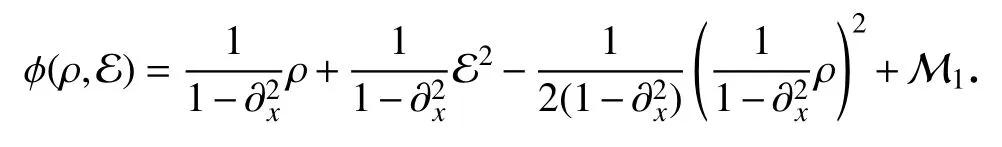
进一步，令

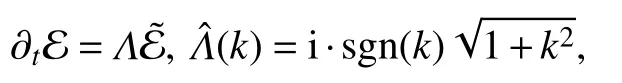
其中s gn(k)表示k的符号函数.则由模型(1)的最后一个方程可得

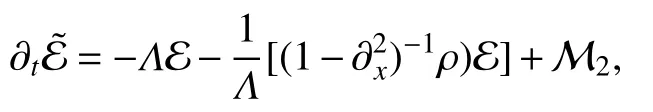
其中M1,M2是三次及高于三次的非线性项，均有很好的性质.此时，可将方程(1)重新书写为一阶偏微分方程组，并将其线性项、二次项以及高次项分开：

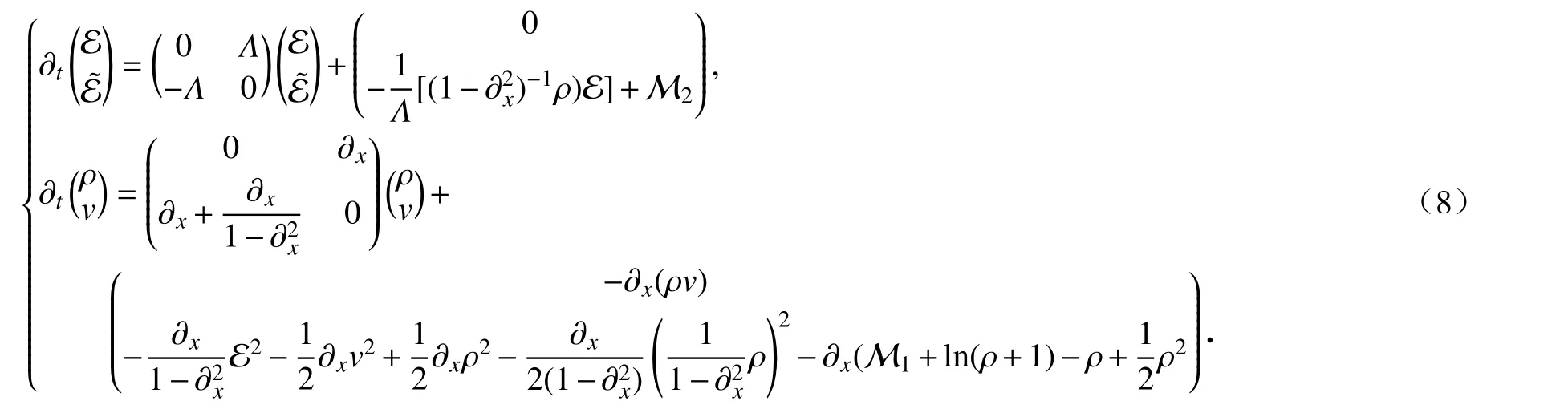
下面通过变量替换，将式(8)的线性部分进行对角化处理.令

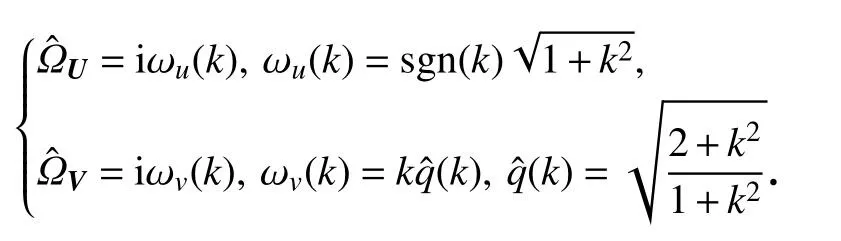
将式(9)代入式(8)可得以下对角化方程组：

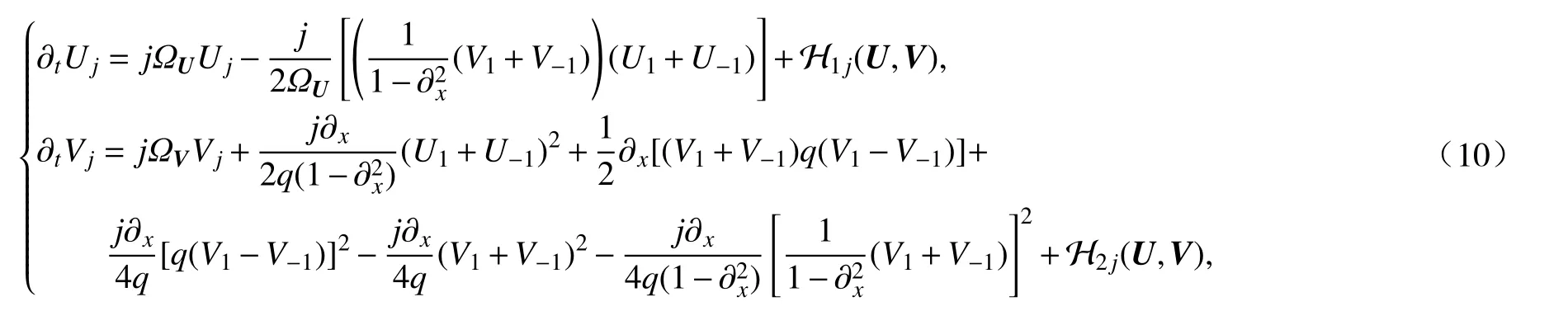
其中j∈{±1}，H1j(U,V),H2j(U,V)是关于U,V的三次及高于三次的项，且不会损失导数，因而有比较好的估计.

下面从对角化方程组(10)出发，形式推导NLS 方程.做如下渐近展开：

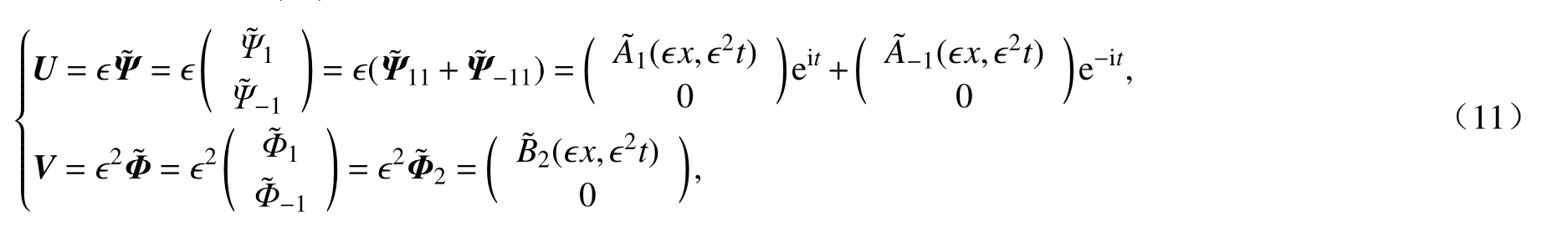
其中A±1为复值函数，且满足=A-1，B2为实值函数.将渐近展开式(11)代入对角化方程(10)并取 ϵ的各阶系数为零.在这个过程中，遇到如的项，可将 ωu(k)以 及(k)在k=0处Taylor 展开.令 ϵ3eit的系数为零，可得

令 ϵ3的系数为零，可得

为了证明NLS 方程(14)的逼近性质，需要考虑下列余项：这些余项就是将渐近展开式(11) 代入对角化方程(10) 之后所有未被消掉的项.通过对形式逼近解进行以下两方面的修正，可以使余项任意小，进而有利于后面对误差进行一致能量估计.首先，将式(11)从形式上展开到关于 ϵ更高阶的项，形式上如式(15).实际上，展开到高阶之后代入方程(10),类似的方法可得(p=2,3,4) 满足线性非齐次Schrödinger 方程.该方程的系数函数和自由项依赖于，且(q=3,4,5)满足依赖于的代数方程，具体推导过程这里不再赘述.其次，利用截断函数使逼近解在Fourier 空间中具有紧支集，且集中在k=0的某个小邻域内.通过对逼近解进行这两次修正，可以证明余项任意小，并且修正后的逼近解与修正前的逼近解差值很小.另外，第二步修正使得逼近解成为解析函数，从而对误差的能量估计更有利.此修正过程也可参考文献[20].具体地说，修正后的逼近解(记为(ϵΨ,ϵ2Φ))有下列形式：

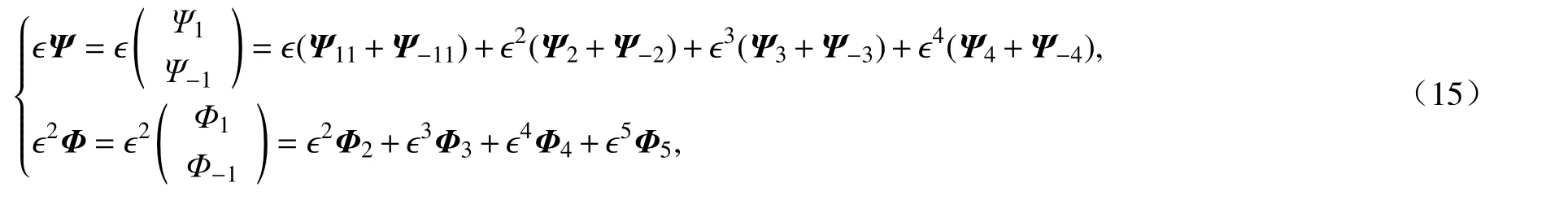
其中

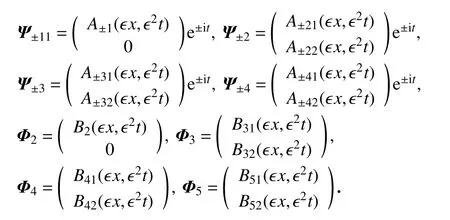
引理5令sA≥6，设∈C([0,T0];HsA(R,C))是NLS 方程(14)的解，且满足

则对所有的s≥0，存在依赖于CA的常数CRU,CRV,CΨ,CΦ,ϵ0，使得对所有的ϵ ∈(0,ϵ0)，逼近解(ϵΨ,ϵ2Φ)满足

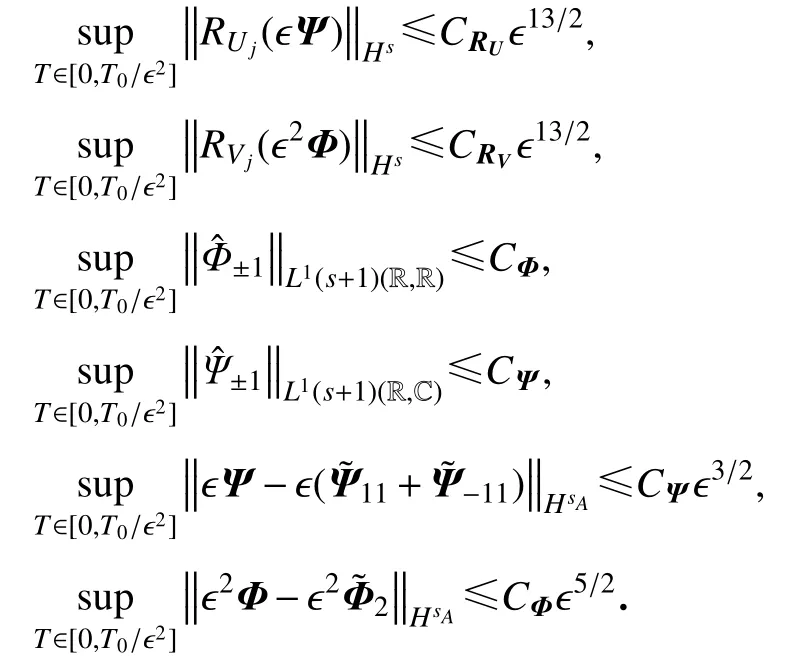
引理5的证明可参考文献[20]中的引理5.事实上，前4个估计式成立的原因是修正逼近解 (ϵΨ,ϵ2Φ)在Fourier 空间中有紧支集.又由于对于所有的m,M≥0有

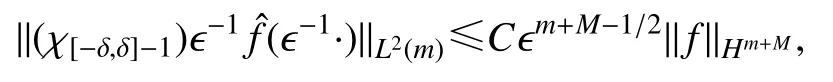
其中χ[-δ,δ]是作用在[-δ,δ]上的特征函数.引理5 中第三和第四个估计式经常被用来估计下式：

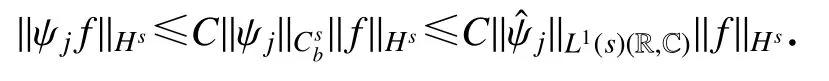
引理6[20]对所有的s≥0，存在常数C＞0使得下式成立：

3 Normal-form 变换

为了严格证明NLS 逼近，需要对误差作一致能量估计.为此，先推导误差满足的发展方程.根据第2 节得到的修正逼近解ϵ Ψ,ϵ2Φ，可设模型(10)的真实解有下列形式：

其中j∈{±1},β=将式(17)代入方程(10)中可得误差(R,S)满足的发展方程为

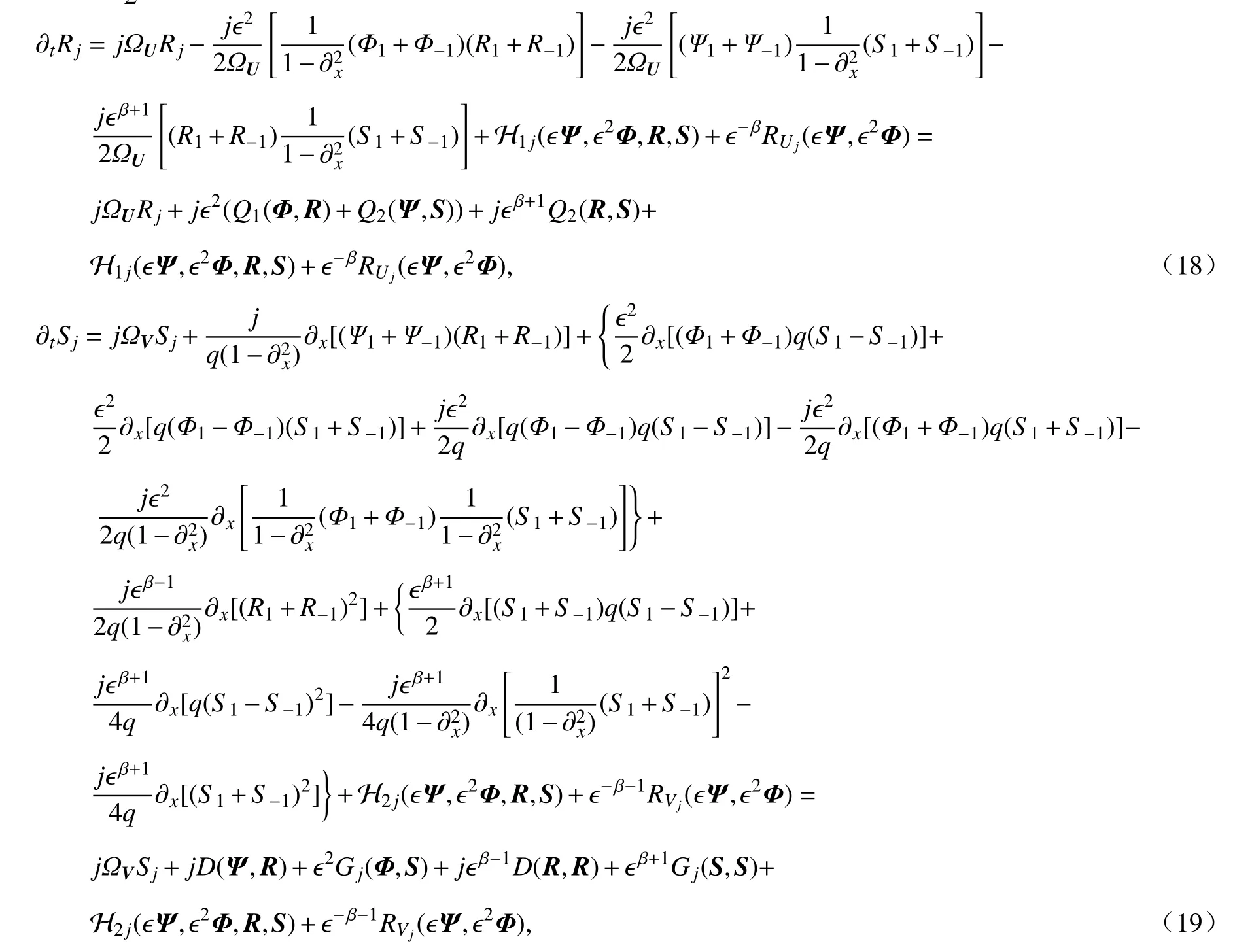
其中q满足对于误差方程(18) 和(19)，线性算子 ΩU和 ΩV生成一致有界半群，因而不会产生困难.根据引理5 中的估计式以及 β的取值可知，余项满足

ϵ-βRUj=O(ϵ4),ϵ-β-1RVj=O(ϵ2).

由引理5 中逼近解的估计以及方程(10)中 H1j,2j的特点可知

H1j,2j(ϵΨ,ϵ2Φ,R,S)=O(ϵ2).

另外，二次项满足

ϵ2(Q1(Φ,R),Q2(Ψ,S),Gj(Φ,S))=O(ϵ2),

ϵβ+1(Gj(S,S),Q2(R,S))=O(ϵβ+1),

ϵβ-1D(R,R)=O(ϵβ-1).

因此，为了在时间尺度 O(ϵ-2)上得到NLS 逼近的有效性，只有误差方程(19) 右端第二项即jD(Ψ,R)=∂x[(Ψ1+Ψ-1)(R1+R-1)]需 要被消去，使其成为O (ϵ2)项.下面利用normal-form 变换消去该问题项，令

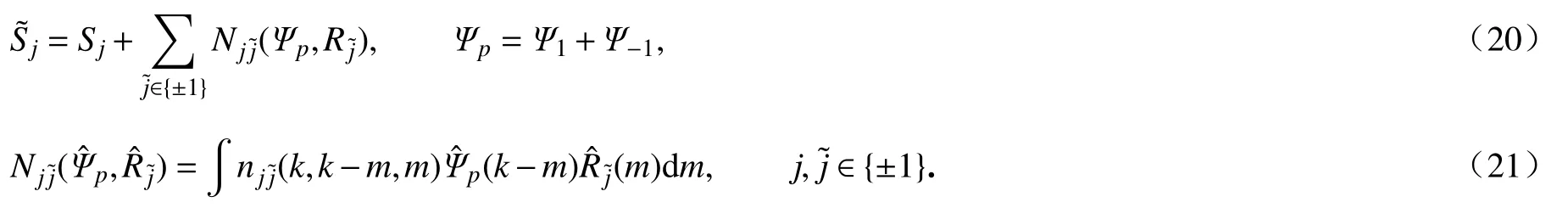
引理7Normal-form 变换(20)有以下性质：

① Normal-form 变换的核函数满足

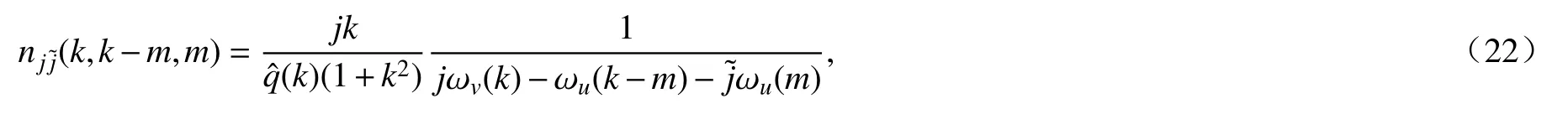
且下列等式成立

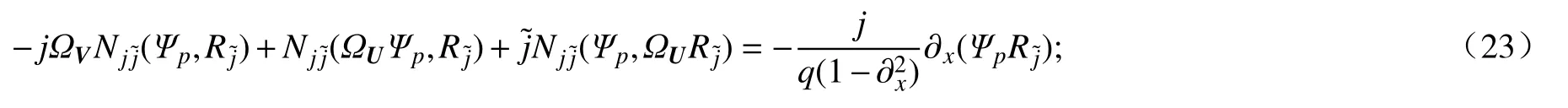
② 对于任意的s≥6，存在常数C，使得

证明将normal-form 变换(20)代入关于误差S的发展方程(19)中可得

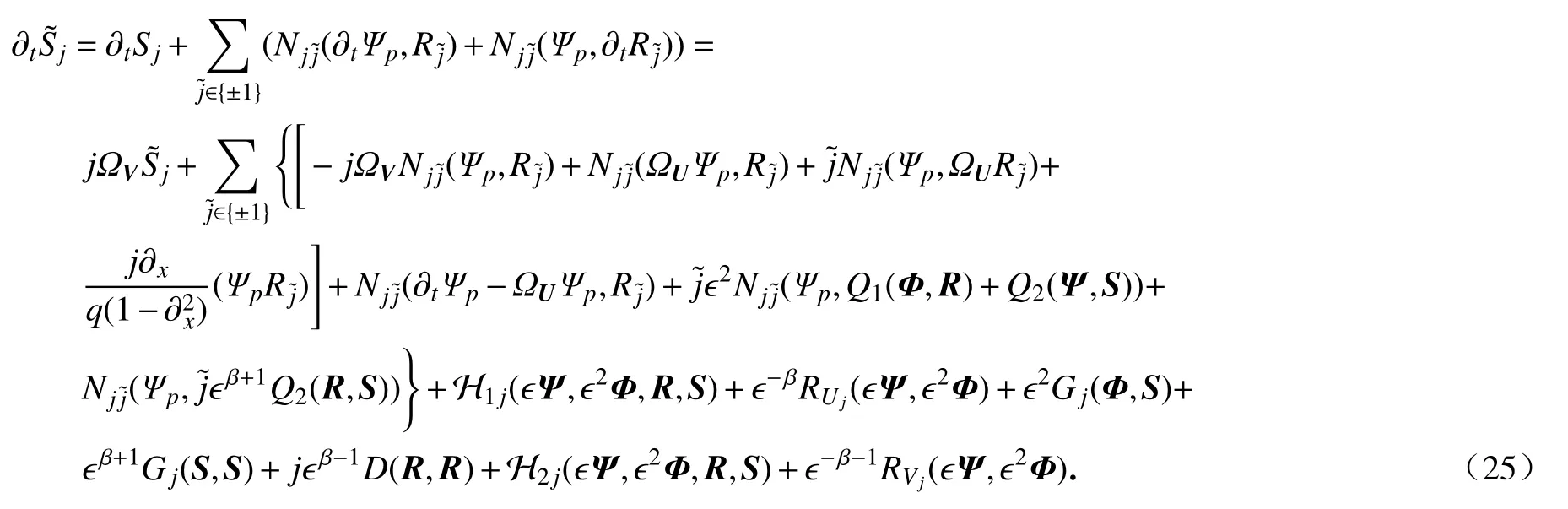
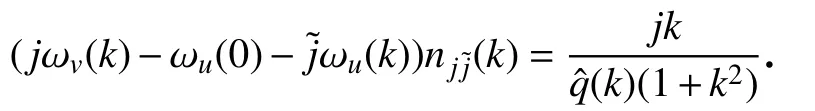
故可定义(k)为

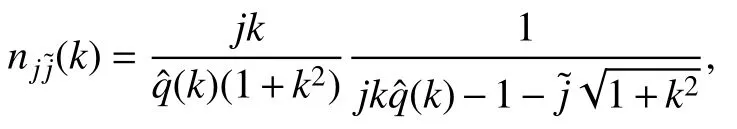
注意到当k=0,=1时，分母确实为零，也就是说k=0是一个共振点，但由于二次项在k=0也为零，因此k=0为平凡共振点.除此之外，无其他共振点.因此，此处所做的normal-form 变换是有意义的，可以成功消去误差方程中的O (1)项，引理7的第①条得证.根据引理5 关于逼近解的估计以及normal-form 变换的核函数的形式可以直接得到估计式(22)，引理7的第②条得证.

4 误差估计

将normal-form 变换(20)代入误差方程(18)和(19)中，得到变换后的误差方程为

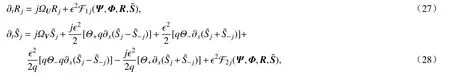
其中

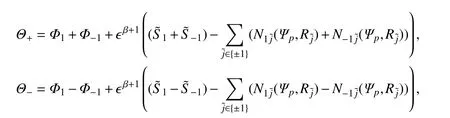
其中F1,F2表示不损失导数的项，即对于所有的s≥6有下列估计

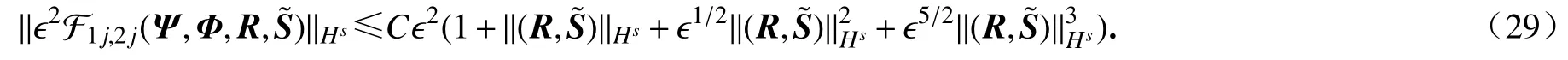
为了严格证明NLS 逼近的有效性，只需要得到误差 (R,)在 时间尺度 O (ϵ-2)上的一致能量估计.由于误差方程(28)中二次项损失一阶导数并且有交叉项，故首先介绍以下引理.

引理8误差方程(28)的两个分量方程作差可得

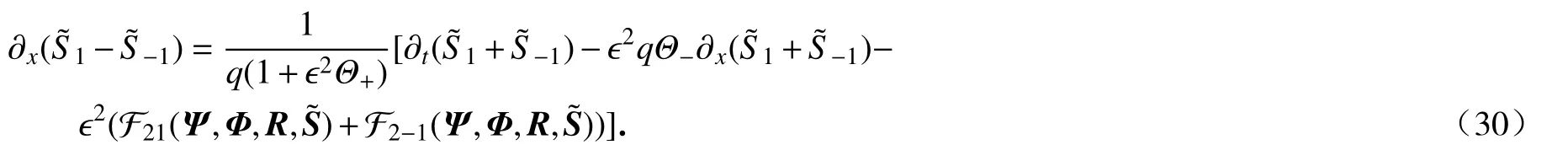
下面对误差作能量估计.设

现在分析∂tMℓ.经过计算可得

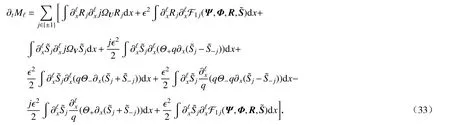
由于色散算子 ΩU,ΩV是反对称微分算子，因而等式(33)右端第一项和第三项均为零.又根据估计式(29)、引理5、Cauchy-Schwarz 不等式、Sobolev 嵌入H1L∞以及Young 不等式可得，等式(33)右端第二项和最后一项可以被控制.对等式(33)进一步利用交换子的定义(6)，可得

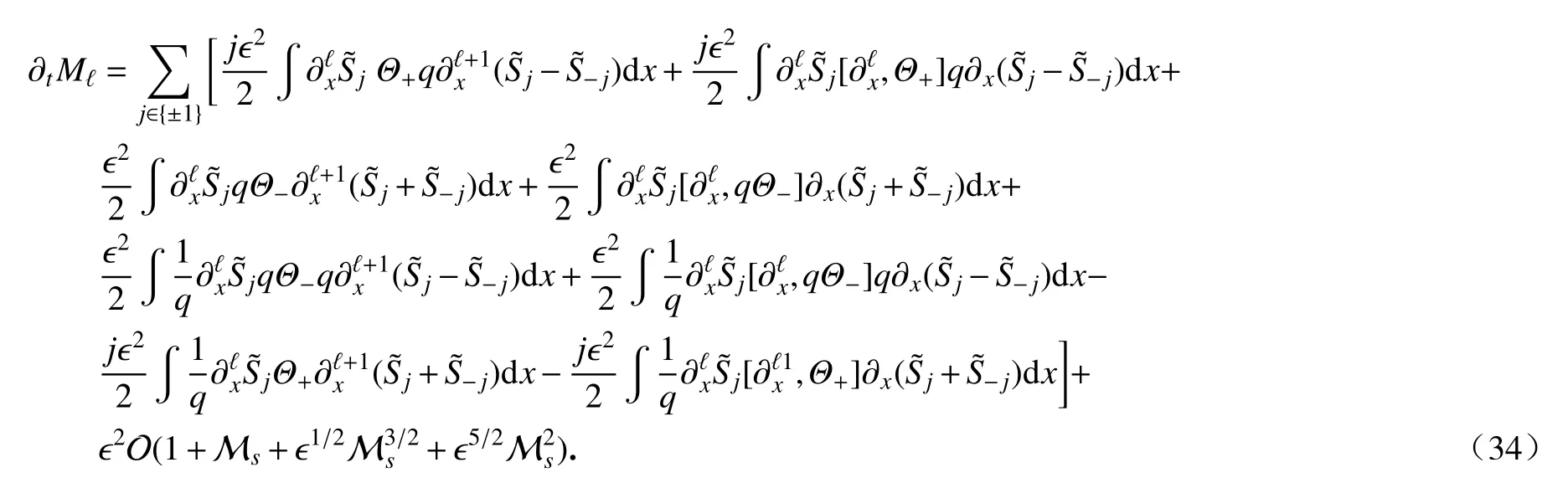
回顾式(3)可知，当|k|→∞时，有

对式(34)，利用式(35)、式(30)、分部积分、交换子估计(7)、引理5、Cauchy-Schwarz 不等式、Sobolev 嵌入H1L∞以及Young 不等式可得

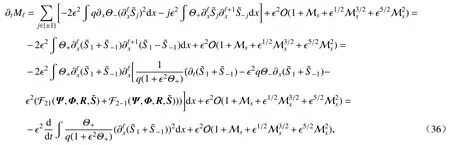
因此，可以定义如下形式的修正能量泛函：

其中

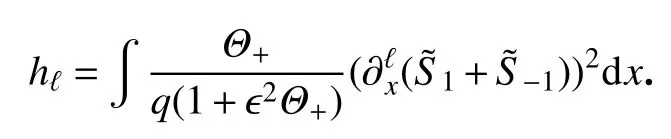
对于封闭的能量估计式(38)，利用Gronwall不等式可知，对于足够小的ϵ＞0，在t∈[0,T0/ϵ2]上是一致有界的.另外，根据normal-form 变换(20)及其估计(22)可得，因此，对角化模型(10)的真实解与修正逼近解 ϵΨ,ϵ2Φ 之间的误差 (R,S)在t∈[0,T0/ϵ2]上是一致有界的.进一步地，根据引理5 中关于逼近解的估计，以及可逆变换(9)可得定理1的结论.

5 结论与展望

本文研究了一类双流体模型的调制逼近，其中调制逼近解是关于时间震荡的正弦波列.在严格证明该调制逼近的有效性时，模型中拟线性二次项会引起平凡共振点k=0的出现以及导数的损失.本文通过利用normal-form 变换并构造合适的修正能量泛函，最终在时间尺度O (ϵ-2)上严格证明了误差的一致能量估计.若考虑关于时空的震荡逼近解，则证明调制逼近过程中还会出现两个非平凡共振点.寻找合适的权重函数有望解决非平凡共振点引起的困难，笔者拟将另文探讨.

致谢本文作者衷心感谢山西财经大学青年基金项目(QN-202021)对本文的资助.