A Sufficient Condition for the Noncorrelation of Binary Pattern Sequences
ZHENG Yu(郑妤) ,LUO Xueming(罗学明)
(1.School of Information and Mathematics,Yangtze University,Jingzhou 434023,China;2.School of Computer Science,Hunan University of Technology,Zhuzhou 412007,China)
Abstract:We research the noncorrelation of binary pattern sequences in this paper.By means of careful analysis of the law of correlation function,we obtain a intuitive result which is a sufficient and non-necessary condition for the noncorrelation of degree-k binary pattern sequences,and it is the extension of the results of the noncorrelation of degree-3 binary pattern sequences.
Key words:Noncorrelated;Spectral measure;Pattern sequences
1.Introduction
A monorail system with a sequence of left shift operator is a symbolic dynamical system whose spectral properties depend on the combination properties of the original sequence.If the Fourier spectrum of the sequence is the Lebesgue measure,the sequence is called noncorrelated[1].In this case,the correlation function which is transformed by the Fourier transform into the spectral measure of dynamical system takes value 0 at any nonzero integer number and the sequence has the highest aperiodicity.Of course,there are so many sequences are not noncorrelated,such as the spectral measure of Ture-Morse sequence is singular continuous,which is studied by Zaks,Pikovsky and Kurths[2].More properties of this sequence in dynamical system are researched by PENG and Kamae[3].Them-multiplicable sequences also have singular spectral measure,which is discussed by NIU and WEN[4].
For a positive integerkand natural numbern,letP ⊂{0,1}k {0}kande(P,n) be the number ofPin 2-adic representation ofn.DefineSn=(-1)e(P,n),∀n∈N,we callS={Sn}n≥0∈{1,-1}Nthe binary pattern sequence with pattern setPof degreekor degree-kpattern sequence for short.
Morton and Mourant defined a class of interesting sequences in [5-6] and they call them arithmetic fractal since these sequences are self-similar and self-generating.For a finite abelian groupE,letENbe the set of concatenation sequencesa=a0a1a2···overE.Denote byΦ2(E)the set of alla∈ENfor which there exists a positive integerMsuch that
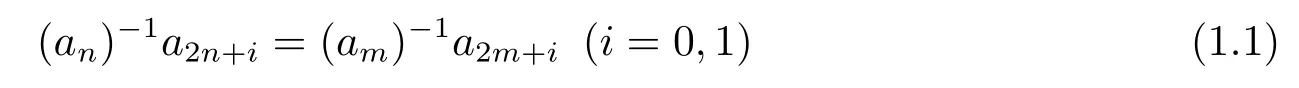
hold for any nonnegative integersn,mwithn ≡m(modM),where the product here is that of the groupE.The modulusMfora∈Φ2(E) is called the conductor ofa.Without loss of generality,we assume thata0is the identity inE.
In [1],ZHENG,PENG and Kamae showed thatSis a pattern sequence with a pattern set of degreekif and only ifS∈Φ2({1,-1}) with the conductorM=2k-1.Also,they considered the correlation functions of binary pattern sequences of degree 3 as well as those with general degrees and special patterns and obtained necessary and sufficient conditions to be noncorrelated.
In [7],ZHENG,PENG and Kamae rewrote the condition in [1] to be a conceptional one independent ofkand apply for the generalk.
In this paper we will continue to discuss the noncorrelated property of binary pattern sequences of general degrees and general patterns and give a more intuitive sufficient condition for the noncorrelation.
An outline of this paper is as follows.In Section 2,we devote to represent some definitions and main result.In Section 3,the details of proof are presented.
2.Preliminary
Throughout the paper the variablesh,i,j,k,l,m,nbelong to natural number set N with 0∈N unless otherwise stated.
We will focus on the noncorrelated property of degree-(k+1) pattern sequencesSwhich satisfySn(S2n,S2n+1)=Sm(S2m,S2m+1),n ≡m(mod 2k),where (S2n,S2n+1) is thenth segment when we divideSinto segments of length 2.
Let’s recall the definition of the correlation function ofSas follows:

It is known that the correlation function of this pattern sequence exists,thus it admits a unique spectral measure[1].
Definition 2.1For any positive integerk,the correlation subfunctions ofS={Sn}n≥0are defined by
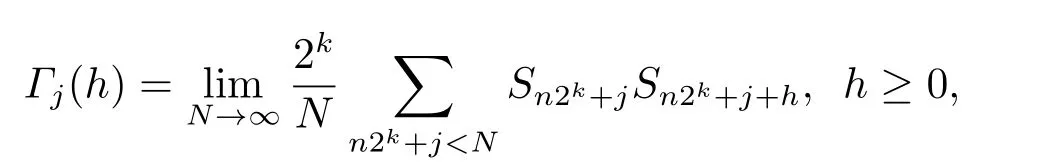
wherej∈{0,1,···,2k-1}.
Remark 2.1The above definition is valid because these limits exist as is shown in [1].Also,
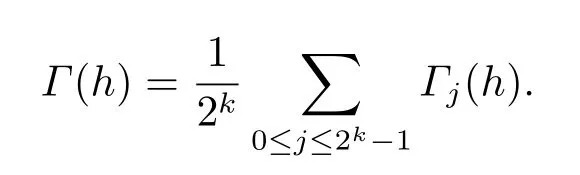
3.Main Result
Theorem 3.1If a degree-(k+1)pattern sequenceSsatisfies=0 wherel=0,1,···,2k-1-1,thenSis noncorrelated.
ProofAccording to the definition of the noncorrelated sequence in [1],the aim is to show the correlation functionΓ(h) is vanished whenh >0.
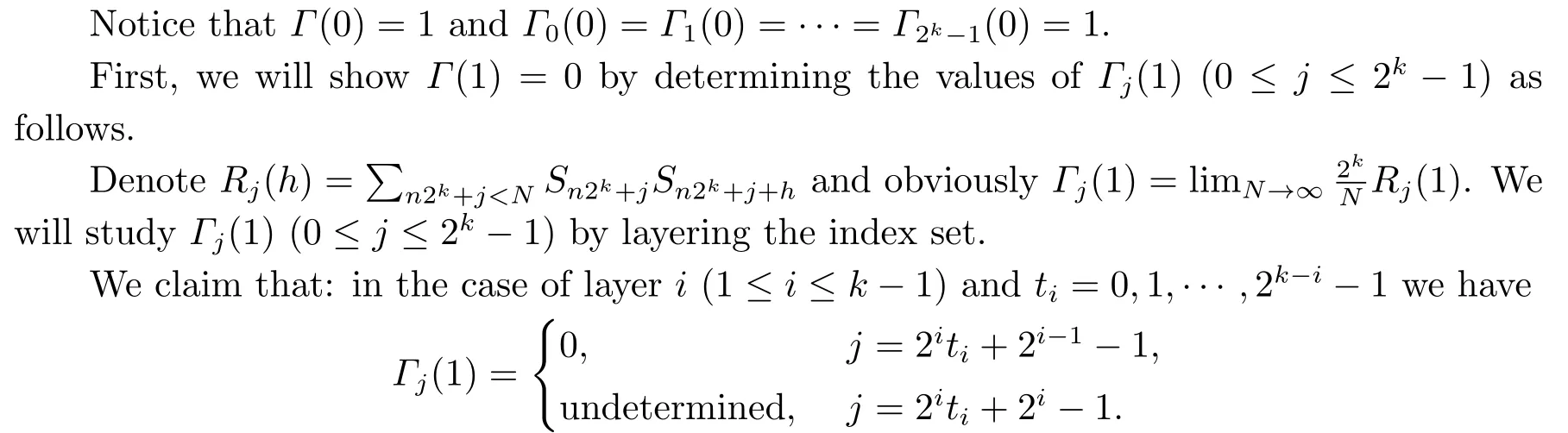
Take the undetermined part in each layer as the next layer,and the process will be terminated by finite induction.The next layer means thei+1 layer for theilayer.
In fact,by recursive formulas about the sequenceS:

Let’s look at the relationship between the subscripts of the correlation subfunction in(*).Asjis odd number which no more than 2k-1,we can get the relationship ofj,(j-1)/2 and 2k-1+(j-1)/2 in Table 3.1.

Tab.3.1
It can be noticed that 2k-1+(j-1)/2 and (j-1)/2 have the same parity.By the result in Layer 1,we can get

Whenmis odd andjis even,that is [(j+m)/2]=[j/2]+(m-1)/2,we get
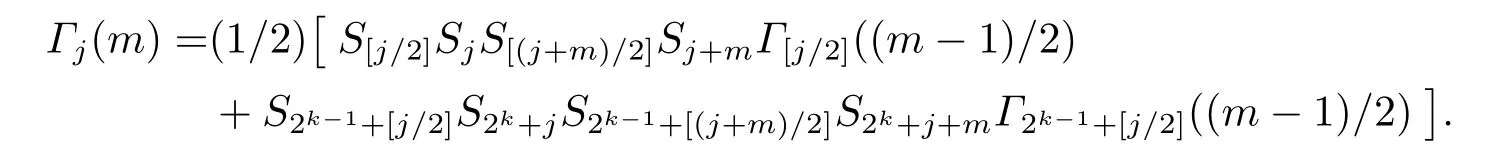
Whenmandjare both odd,that is [(j+m)/2]=[j/2]+(m+1)/2,we have
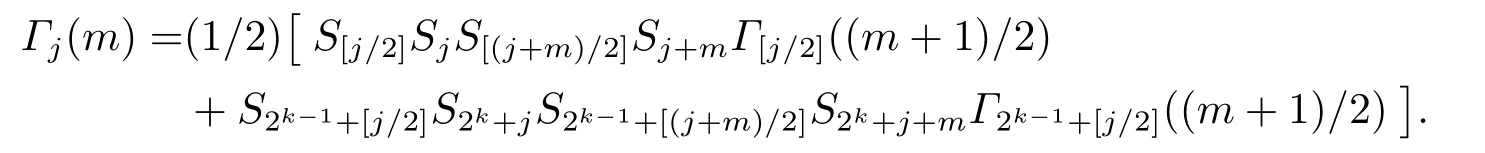
Asm ≥2 we get 1≤m/2<m,(m-1)/2<mand (m+1)/2<m.Then by the induction hypothesis the proof is completed.
Remark 3.1This condition must not be necessary.Whenk=2,it easy to show that the correlation measure of the sequence whose first eight items are (1,-1,1,1,-1,1,1,1) is the Lebesgue measure but it can’t satisfy the sufficient condition.
- 应用数学的其它文章
- 一类线性离散时间系统的预见控制器设计
- Global Boundedness to a Quasilinear Attraction-repulsion with Nonlinear Diffusion
- Trudinger-Moser Inequality Involving the Anisotropic Norm with Logarithmic Weights in Dimension Two
- 关于非齐次树指标m重马氏信源的一个强极限定理
- 相依风险结构下弹性ò休c金产品价Š风险比较
- Superconvergence Analysis of Anisotropic Linear Triangular Finite Element for Multi-term Time Fractional Diffusion Equations with Variable Coefficient

