基于改进适应度函数组合法的机器人逆运动学求解
李 光 谭薪兴 肖 帆 易 静 薛晨慷 于权伟
(1.湖南工业大学机械工程学院, 株洲 412007; 2.武汉科技大学机械自动化学院, 武汉 430081)
0 引言
传统的逆向运动学的求解理论和方法有解析法[1-3]、几何法[4-5]、数值法[6]等。解析法主要以消元的方式将高维方程组转换为低维方程组,PIEPER等[7]提出了一类具有解析解的6R串联机械手,虽不满足Pieper准则的机器人逆向运动学问题,也获得了广泛的研究[8-9],其给出的方法需要进行大量的三角代换,计算过程十分复杂耗时,很难在工业机械手中实现,且一般结构的机械臂无法得到解析解。几何法针对机器人的特殊结构进行简化再求解,一般无法单独使用甚至无法使用[10]。数值法可以精确搜索到一组逆解,求解速度与初始值相关,甚至存在无解,且数值法需要的运算量大,不适合实时求解的场合[11]。
近年来,利用智能算法求解机器人逆向运动学的方法取得一定的成果[12-20]。神经网络算法的计算代价高,计算能力很大程度取决于数据的量,同时也取决于网络的深度和复杂程度;遗传算法全局搜索能力强,局部搜索能力较弱,容易误入局部最优解;蚁群算法和鱼群算法参数设置复杂,如果设置不当,容易偏离最优解;粒子群算法和果蝇优化算法操作简单,收敛速度快,在机器人逆向运动学中也得到了应用,但存在提前收敛、维数灾难等问题。自适应协方差矩阵进化策略(Covariance matrix adaptation evolution strategy,CMA-ES)算法[21-22]是在 ES算法[23]的基础上发展而来的无约束优化算法,在全局优化、多峰优化、多目标优化、大规模优化和结构性工程等领域得到了大量应用[24-25],该算法搜索性能较高,并且能够达到比较高的搜索精度。
为克服单一的传统算法和单一的智能算法求解逆向运动学的不足,组合算法引起了许多学者的关注。赵瑜[26]基于布谷鸟算法和牛顿法组合算法求解6R机器人运动学逆解,可以得到较高精度的逆运动学解,求解效率较低;陈禹含等[27]结合旋量理论和代数法的求解逆运动学求解,求解过程较为复杂;裴九芳等[28]采用解析解和数值解求解三指机器人逆向运动学,求解效率较高但通用性较差。
智能算法中适应度函数决定了机器人逆向运动学分析结果的性能,文献[29-31]阐述了建立适应度函数的常用方式,可以高精度地求出逆向运动学解,但是该适应度函数较为复杂,增加了求解时间。
一般结构的机械臂没有解析解,用已有的代数法求封闭解的推导过程十分复杂,而单一的智能算法和组合算法求逆解均存在不足。一般结构机器人是指至少有一组相邻关节轴线相交于一点的机器人[32]。本文提出一种基于分离-重构方法获得智能算法的适应度函数,与解析法相组合的方法求一般结构多自由度机械臂运动学逆解。利用分离-重构的方法[33],构建分离-重构适应度函数,求解出部分关节角,最后利用解析法求解余下的关节角。选用改进的CMA-ES算法[31]验证分离-重构适应度函数,以验证方法的有效性。在一般结构多自由度机器人上进行仿真,在相同条件下的点对点运动中,使用改进适应度函数的组合法和原方法求解,同时为模拟复杂程度不同的工作环境,对二维和三维空间中的连续轨迹进行跟踪,比较组合法和原方法的求解精度和关节角运动平稳性;在具有一般结构的REBot-V-6R机器人实验平台上进行三维空间连续轨迹的跟踪实验。
1 适应度函数与解析法
1.1 适应度函数
目前,DH法是机器人运动学常用的建模方法,可以确定机器人的关节参数和关节变量,它与机器人结构顺序和复杂程度无关,通过齐次变换矩阵描述两个相邻坐标系间的空间位姿关系。
首先建立连杆坐标系,然后通过4次旋转平移变换,根据DH参数,定义第i连杆的参数ai为连杆长度,αi为相邻两关节轴线的夹角,di为第i根连杆和第i-1连杆的偏置距离,θi为第i连杆的旋转角。变换过程顺序如下:绕zi-1轴旋转θi,沿zi-1轴平移di,沿xi轴平移ai, 绕xi轴旋转αi, 可得到机器人连杆i坐标系相对于连杆i-1坐标系的变换矩阵

(1)
式中R——4×4的旋转矩阵A——移动矩阵
式中s表示正弦函数,c表示余弦函数。
根据式(1)得到一般结构多自由度机器人正向运动学数学模型,通过正向运动学控制机器人末端执行器到达指定位置,末端位姿齐次变换矩阵为
(j=1,2,…,n)
(2)
式中p——3×1位置向量
a——3×1接近向量
为了建立分离-重构适应度函数,需要对具有一般结构的多自由度机械臂按一定方式进行分离-重构:在相邻轴线交点处进行分离-重构,相邻相交轴的坐标系如图1所示,子链i和i+1交于点O。分离后为使两子链重构,需使得两子链的末端位姿一致。首先根据重构后两子链末端位置约束条件,建立约束等式
pi=pi+1
(3)
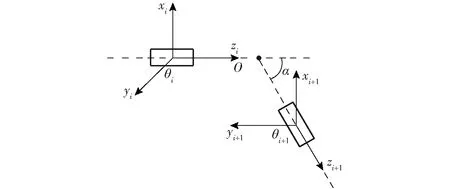
图1 相邻相交轴的坐标系Fig.1 Coordinate system of adjacent intersecting axes
两子链z轴之间夹角为α,在实际应用中,α一般不等于0,为使子链i绕xi轴旋转-α,使子链i和i+1的z轴重合,建立约束等式
(4)
根据分离-重构点位置不同,一般结构自由度n机器人有n-1种情况,以一般结构六自由度机器人为例,交点O有5种位置情况:关节轴1和轴2的交点、关节轴2和轴3的交点、关节轴3和轴4的交点、关节轴4和轴5的交点、关节轴5和轴6的交点,结合齐次变换矩阵式(2)可以得到以下5种情况
(5)
(6)
(7)
(8)
(9)
确定了分离-重构点位置,在式(5)~(9)选择一种合适的情况,将坐标变换矩阵式(1)代入,得到两子链的展开式Ti和Ti+1,对应式(2)中p、a矩阵的位置,根据位姿约束得到式(3)、(4),完成构建分离-重构适应度函数
(10)
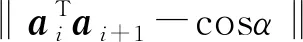

图2 组合法流程图Fig.2 Flow diagram of combination method
在文献[29-31]提出的算法中,使用位姿误差建立适应度函数JPP求解逆运动学,JPP表示两种误差范数之和,计算式为
JPP=‖pdes-pcur‖+b‖Rdes-Rcur‖
(11)
式中R——3×3的旋转矩阵[34]
b——罚函数
其中‖pdes-pcur‖表示位置误差范数, ‖Rdes-Rcur‖表示姿态误差范数,使用智能算法直接求出全部关节角,该方法的流程图如图3所示。

图3 原方法流程图Fig.3 Flowchart of original method
JPP中包含全部关节变量,比JDR多2个关节变量,JPP求解过程复杂,R是一个3×3的旋转矩阵,而a是3×1的姿态矩阵,JPP的代数式维度更大,通过推导得到的代数式更复杂,在智能算法中求逆解时会明显增加耗时。
除此之外,JPP中还需设置位置误差函数的罚函数b,是为了保证姿态误差‖Rdes-Rcur‖和位置误差‖pdes-pcur‖在求解过程中处于同一数量级,防止局部收敛和发散等情况[35],但JDR不存在这种情况。
1.2 解析法分析
通过求解JDR,确定了多自由度机械臂非相邻相交轴线的关节角,再通过解析法求解剩余的两个关节角,避免了全部采用解析法求解的繁琐复杂,解析法求解的两个关节角和智能算法求解出的其他关节角精度在同一数量级。机械臂已经确定了非相邻相交轴线的关节角,则两子链末端的αi和αi+1将保持不变,即zi轴和zi+1轴的位姿确定,根据几何约束条件知αi和oi+1之间成π/2-α,故可以得到
(12)
式(12)展开后,只有θi+1未知,因此可以通过简单的数学计算解得,且θi+1只有一个解。旋转坐标系关系图如图4所示。
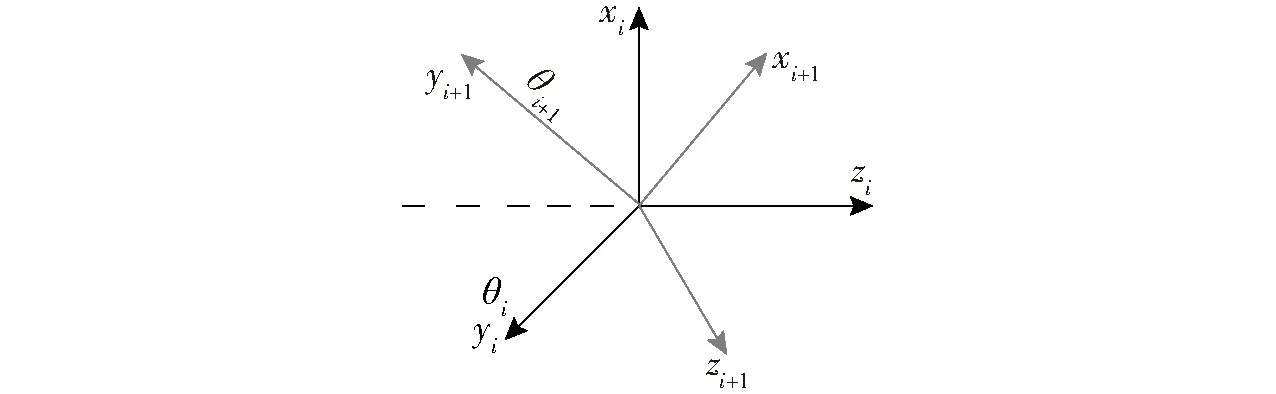
图4 旋转坐标系关系图Fig.4 Relationship of rotating coordinate system
θi+1在周期内绕zi+1旋转,只有当轴yi+1位于zizi+1平面内才能满足约束条件,因此在一个旋转周期内,θi+1只有一个解。同理,oi和αi+1之间呈π/2+α,故可以得到
(13)
式中只有θi未知,θi也仅有一个解。使用解析法求剩下的θi+1和θi,只需求解两个一元一次方程,求解过程简单方便,解决了使用解析法求一般结构机器人逆运动学解计算繁琐复杂的问题。
2 改进的CMA-ES算法
2.1 算法原理
CMA-ES算法是一种进化策略算法,采用正态分布N(m,C)生成一定数量的搜索种群,N(m,C)表示:搜索分布均值为m,以协方差矩阵为C的多元正态分布,且C=BDBT,其中BB=I,D为对角矩阵,化简多元正态分布N(m,C)得
N(m,C)~m+N(0,C)~m+BDN(0,I)
(14)
式(14)的“~”表示服从相同的分布,由式(14)的逆序可知,I确定等概率密度圆球面,通过B、D的变化可以确定C的椭球面;球面的分布尺度由D中的对角元素决定,主轴的方向由B确定,变化B、D实现球面的分布旋转。
2.2 算法步骤
步骤如下:
(1)参数设置及初始化、静态参数[36]。
(2)突变,突变的目的是使个体之间产生差异。CMA-ES算法的突变过程是以当代的均值为中心,产生下一代种群。
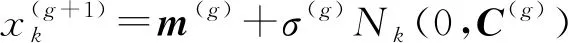
(k=1,2,…,λ)
(15)
m(g)——第g代种群中适应度排名前μ个个体的加权平均值
σ(g)——第g代种群进化步长
C(g)——第g代种群进化协方差矩阵
μ——父代数量
(3)选择和重组,CMA-ES算法采用(μ,λ)策略,父代不参与当前代的适应度排名竞争,优秀个体只从当前子代中选择,对λ个子代进行适应度评价,根据适应能力由高到低排序,选取适应能力强的前μ个个体,作为下一代种群的父代,更新策略参数m(g)、σ(g)、C(g),以此来传递优良的基因,其过程如下:
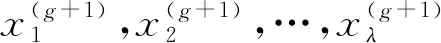
②协方差矩阵自适应调整。
③全局步长控制
(16)
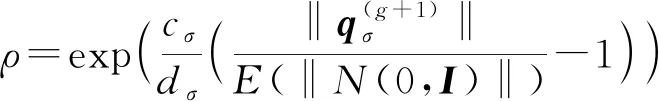
(17)
式中μeff——方差有效选择质量
ε——缩放系数
ε的主要作用是:当代个体中存在越界行为时,在下一代个体更新中,及时阻止越界行为,保证结果在要求范围内,而ε<0.56容易导致出现“早熟”或者无法收敛;ρ可看作步长变化的伸缩因子,δb表示越界敏感因子,个体每个维度在不可行域内出现次数的总和,即不在关节范围内的次数总数,cσ为qσ更新学习率,dσ为接近于1的阻尼系数,E‖N(0,I)‖为归一化进化路径在随机选择下的期望长度。
(4)判断是否达到最大迭代次数或精度,若是,则停止,输出最优解和最优决策向量,否则返回步骤(2),算法求解详细流程如图5所示。
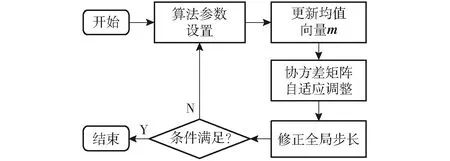
图5 改进的CAM-ES算法流程图Fig.5 Flowchart of improved CAM-ES algorithm
3 仿真实验与结果分析
3.1 适应度函数求解
使用改进适应度函数的组合法和原方法对一般结构FANUC CRX-10iA型协作机器人进行逆向运动学计算。图6为FANUC CRX-10iA型机器人结构简图,可以看出是一般结构的机器人,且不满足Pieper准则,无法得到逆向运动学的完备解析式,表1为机器人连杆参数。

图6 FANUC CRX-10iA型机器人结构简图Fig.6 Structure diagram of FANUC CRX-10iA robot
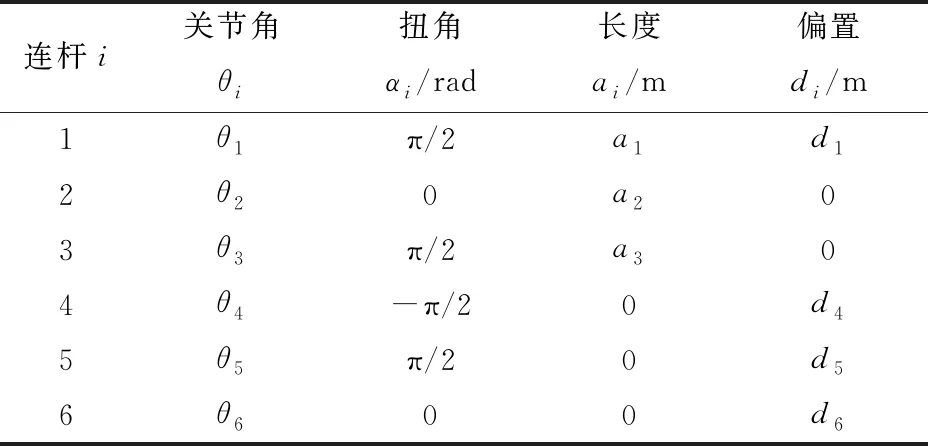
表1 机器人连杆参数Tab.1 Link parameters of robot
根据1.1节中对两种适应度函数的分析,由图6可得关节4和关节5相交于一点,JDR计算式为
(18)
经过计算,建立
(19)
其中a1=0.1 m,a2=0.29 m,a3=0.121 m,d1=0.32 m,d4=0.31 m,d5=0.1 m,d6=0.111 5 m,使用适应度函数JDR求解出θ1、θ2、θ3和θ6,通过解析式(12)、(13)求解相邻相交两轴的θ4和θ5,可得计算式为
(20)

(21)
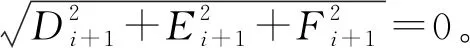
3.2 改进的CMA-ES算法参数设置
使用改进的CMA-ES算法验证分离-重构适应度函数,设置算法的种群数量λ=100,优秀个体μ=50,初始步长σ=0.5,初始均值在0~1内随机产生,求解过程中,前一个逆向运动学解作为当前初始点均值,初始均值缩放系数ε=0.65,算法停止条件为进化次数G=100或者适应度函数J≤10-6。
3.3 点到点运动仿真
在工作空间内,机器人从指定初始位置θ=[0 0 0 0 0 0] rad运动到指定目标关节位置:θ=[0.82 0.93 0.66 0.73 0.88 0.99] rad,分别使用组合法和原方法求解,独立运行50次仿真结果如表2所示,算法收敛情况如图7所示。结果表明,同原方法比较,组合法的求解速度更快更稳定。组合法迭代次数在40次以前就能完全满足精度要求,且大部分迭代次数在25~30次之间收敛,而原方法迭代100次仍然会出现不收敛的情况;组合法的平均求解时间为0.004 s,原方法平均求解时间为0.032 s,速度提升了7倍,从表2的标准差和图7可以看出,组合法求解机器人运动学逆解更稳定。

表2 两种方法独立运行50次结果Tab.2 Results of 50 independent runs of two methods

图7 迭代收敛情况Fig.7 Situation of iterative convergence
3.4 连续轨迹跟踪仿真
为验证组合法在面对不同复杂程度的工作环境时轨迹跟踪的有效性,在工作空间内分别使用二维空间的圆轨迹方程式和三维空间的圆锥螺旋轨迹方程式进行仿真,公式为
(22)
(23)

采用两种方法对空间曲线进行跟踪,结果如表3、4所示,结果表明,在二维平面圆轨迹跟踪上,组合法单点的平均求解时间为0.006 8 s,比使用原方法求解的速度提升4倍左右;在三维圆锥螺旋轨迹跟踪上,组合法速度提升2倍左右。
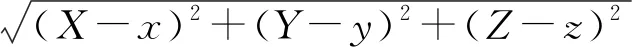

表3 平面圆轨迹跟踪结果Tab.3 Tracking result of plane circular trajectory
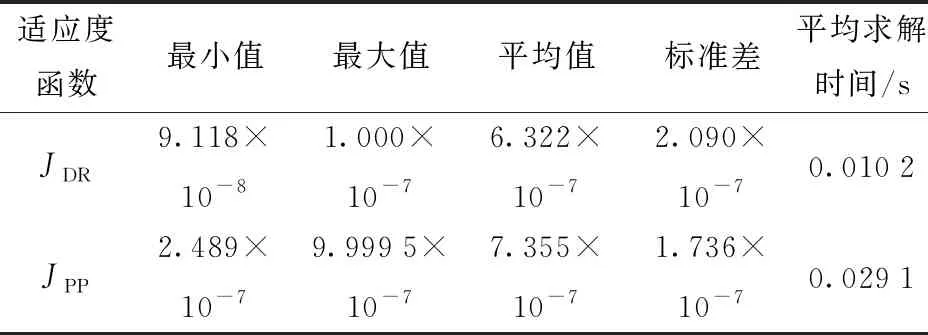
表4 圆锥螺旋轨迹跟踪结果Tab.4 Tracking results of conical spiral trajectory
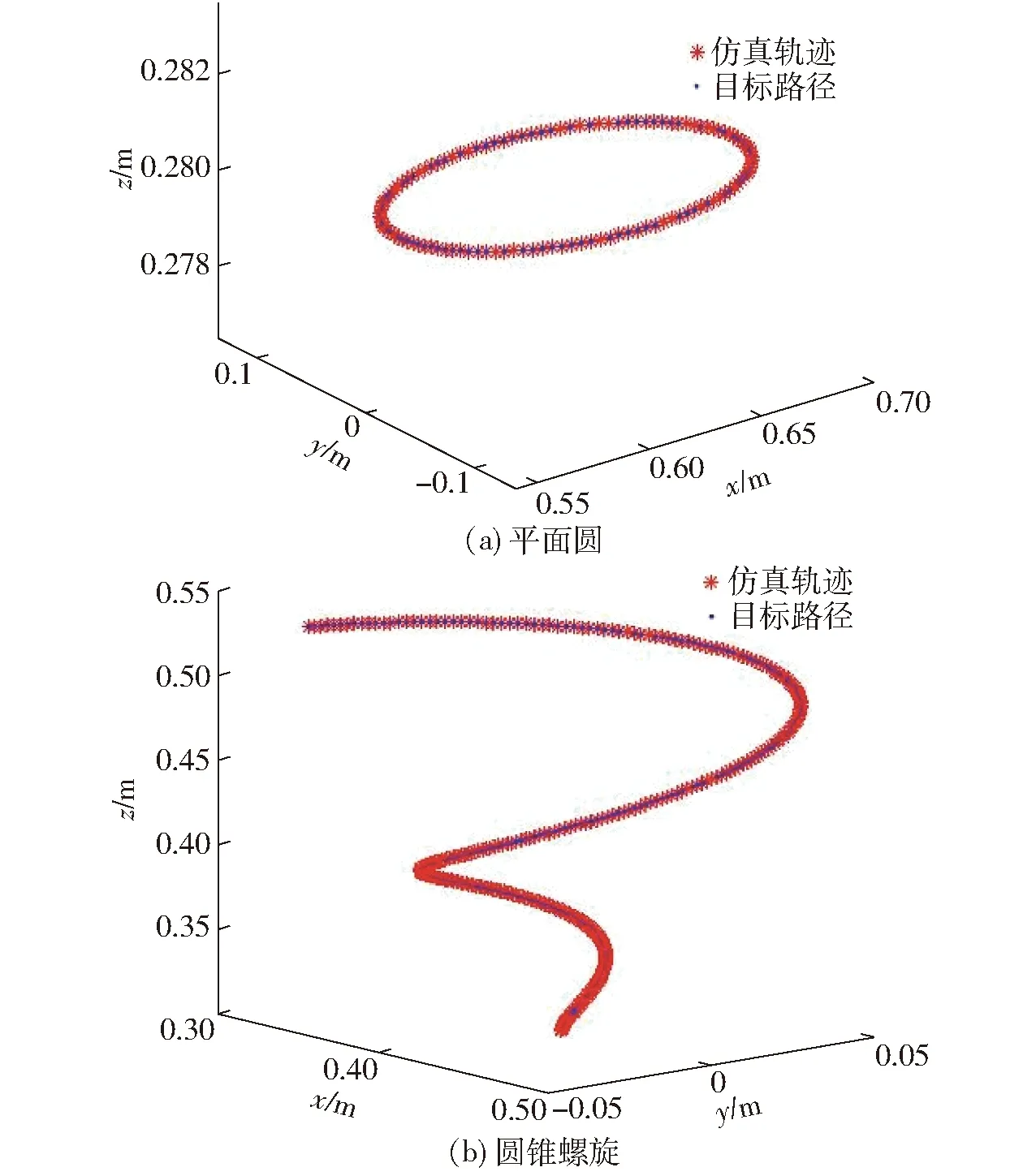
图8 轨迹跟踪Fig.8 Trajectory tracking
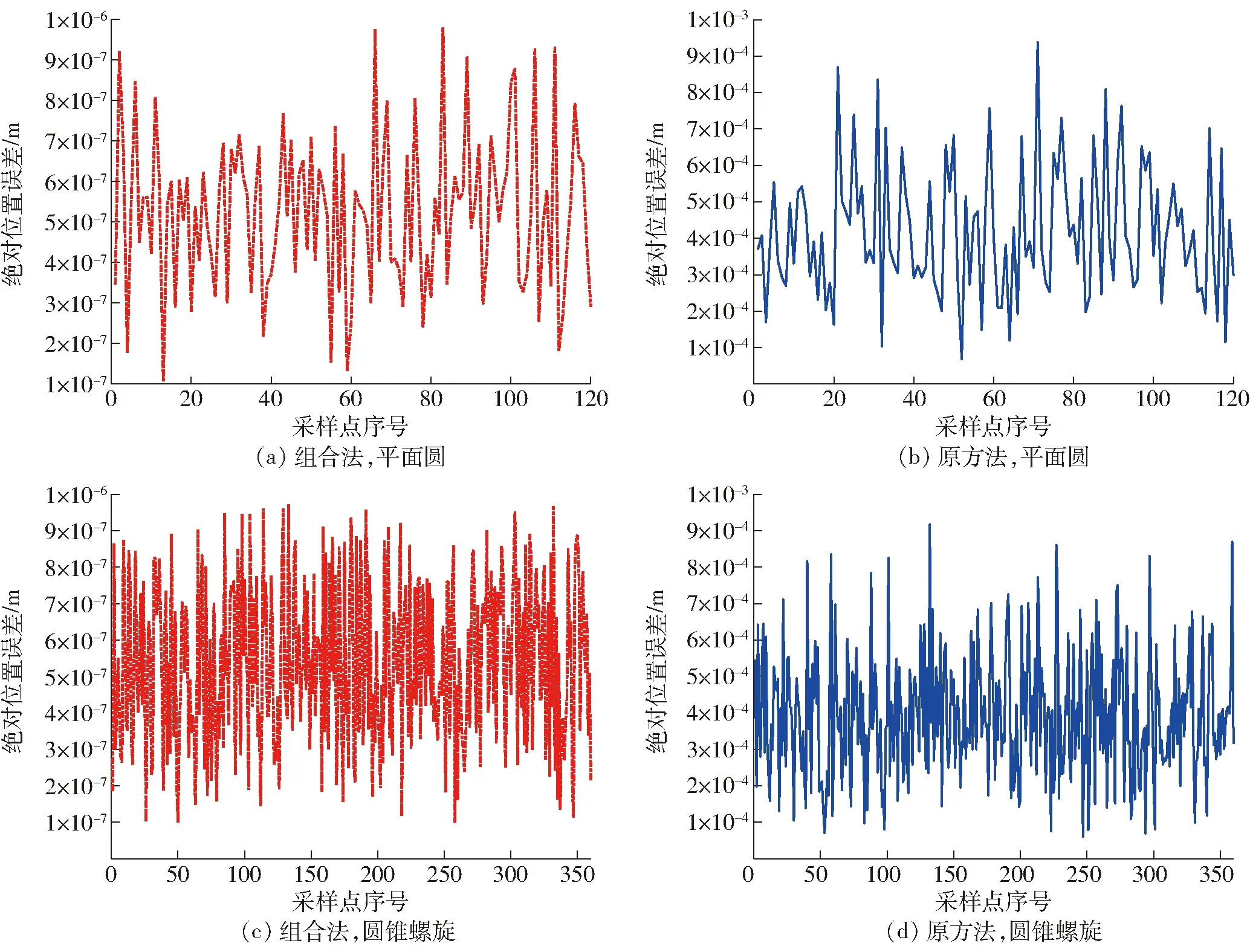
图9 轨迹跟踪误差曲线Fig.9 Error curves of trajectory tracking
图10、11为组合法和原方法连续跟踪两种轨迹的关节角度变化曲线,从图10b和图11b可以看出,原方法在关节角度变化率较大的地方存在锯齿波动,而组合法跟踪过程中关节角曲线平稳光滑。
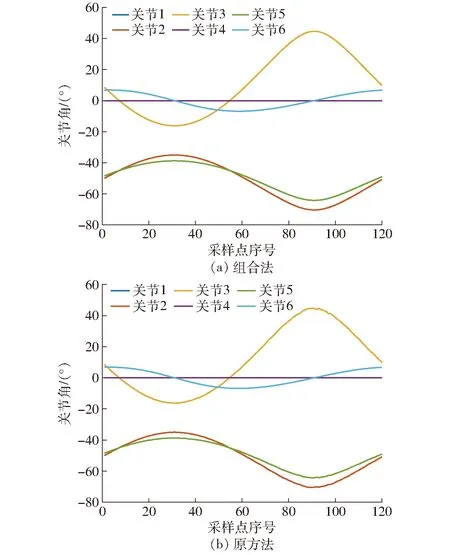
图10 平面圆轨迹关节角变化曲线Fig.10 Changes of joint angle of plane circular trajectory
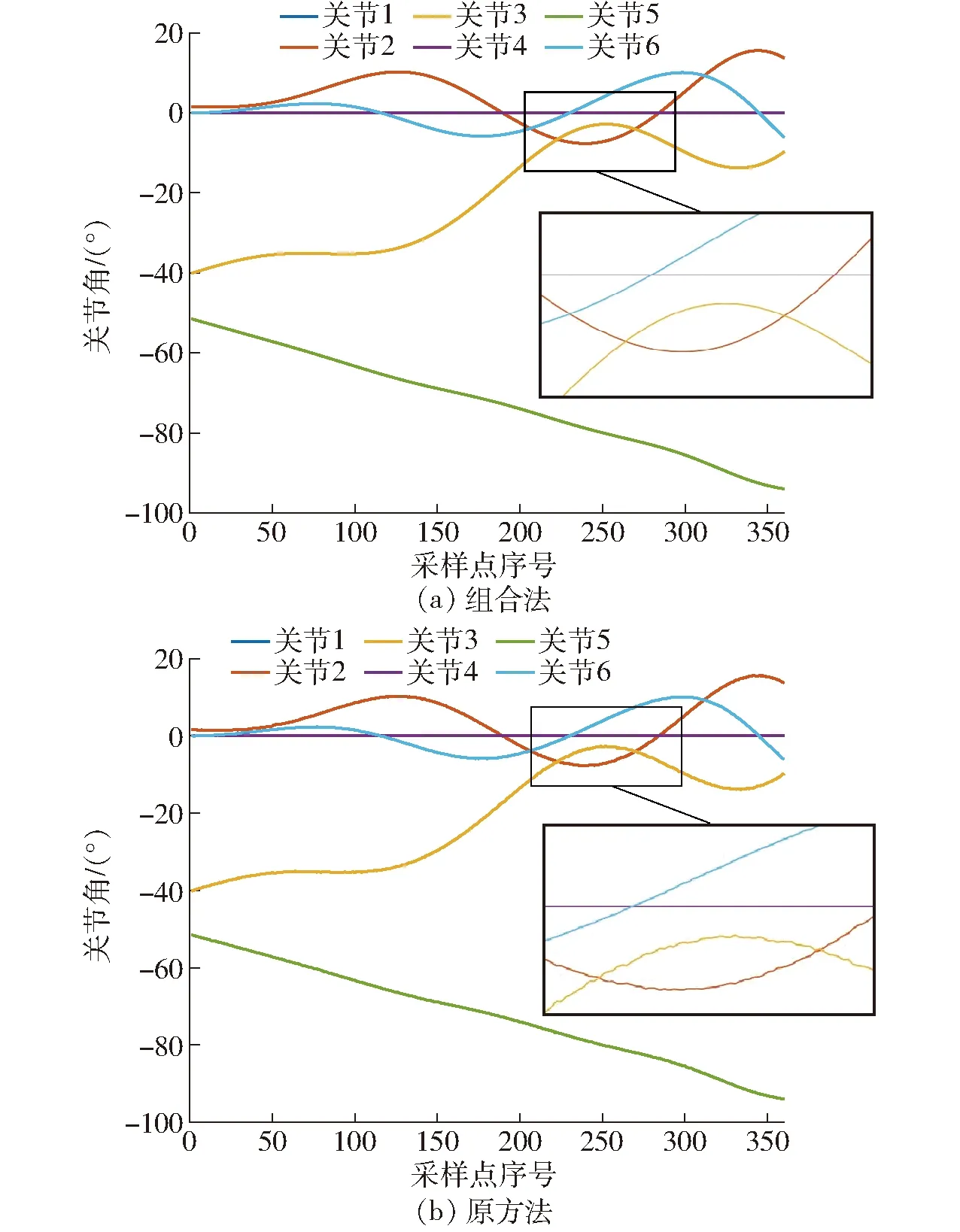
图11 圆锥螺旋轨迹关节角变化曲线Fig.11 Changes of joint angle of conical spiral trajectory
4 实验
以REBot-V-6R型六自由度机器人为实验平台,使用所提的组合法在三维空间中进行轨迹跟踪实验,实验装置见图12,使用VC++6.0搭建的软件环境。

图12 实验装置Fig.12 Experimental device

首先在VC++6.0平台上基于MFC框架编写的程序,将求解的逆向运动学数据转换成各关节对应的脉冲数量,写入软件程序中,通过GALIL运动控制卡提供的函数接口,建立上位机与机械臂之间的通信,然后进行机械臂末端位置标定,最后进行实验。实验过程中各关节运动平稳,顺利地实现了对给定空间轨迹的跟踪,通过计算得到,跟踪误差变化曲线如图13所示,误差结果控制在10-7m数量级,实验结果如图14所示,机械臂末端完全跟踪上了斜圆轨迹,结果表明了改进适应度函数组合法的有效性和准确性。

图13 跟踪误差变化曲线Fig.13 Tracking error

图14 实验结果Fig.14 Experimental results
5 结论
(1)提出了一种智能算法的适应度函数,与解析法组合求解具有一般结构多自由度的机器人运动学逆解,使用分离-重构法建立适应度函数JDR,JDR具有简单可靠的特点,使用改进适应度函数的组合法求逆解,求解速度更优越,求解性能更稳定,轨迹更平滑;在点对点运动求得的逆解中,组合法求解速度比原方法提升7倍左右;为验证组合法在不同复杂环境中的有效性,分别在二维平面圆轨迹和三维圆锥螺旋轨迹进行仿真实验,在两种连续的三维轨迹跟踪中,组合法求解速度比原方法分别提升4倍左右和2倍左右。
(2)在相同条件下,两种方法求解三维连续轨迹的适应度函数值均在10-7数量级,但组合法求解得到的位置精度比原方法高出3个数量级,且组合法不需要设置罚函数;通过在REBot-V-6R型六自由度机器人实验平台上进行三维轨迹跟踪实验,验证了改进适应度函数的组合法在求解一般结构六自由度机器人逆运动学中的有效性和准确性。

