图的高阶谱矩公式

周理泳，薛振宇，吴亚平

(江汉大学 人工智能学院，湖北 武汉 430056)

图的谱理论是代数图论的一个重要研究领域[1]，其研究的主要途径是，通过图的矩阵表示，建立图的拓扑结构和图的矩阵表示的相似不变量之间的联系，从而刻画图的结构特征。

1987年，Cvetkovíc和Rowlinson[2]给出了图的前4阶谱矩的计算公式。文献[3-5]给出图的前8阶谱矩的计算公式。吴亚平等[6]给出单圈图前10阶谱矩计算公式。Chen等[7]研究随机图的谱矩，基于Erdös-Rényi模型，给出图谱矩公式的精确估计。依据谱矩序对图类的排序吸引了许多研究者的兴趣，参看文献[8-14]。章丽丽[15]借助于谱矩，求图中某些子图的个数。本文将给出任意简单图第9阶谱矩计算公式。我们相信有了第9阶谱矩的计算公式，图类依据谱矩序排序又能往前推进一大步。

1 预备知识

本文只考虑简单图，文中出现而未介绍的定义参照文献[1]。设G=(V(G)，E(G))，其中V(G)表示G的顶点集，E(G)表示G的边集，称G是一个|V(G)|-阶图。若G中由顶点和边构成的一个交替序列v0e1v1e2v2…vm-1emvm满足边ei的两个端点为vi-1和vi，i=1，…，m，称此序列为G的一条(v0，vm)-途径。若v0=vm，则称它是一条闭途径。

双圈图具有两种类型的基图(见图1)。记B(p，l，q)是通过在2个点不交圈Cp和Cq之间连一条长为l-1(l≥1)的路v1v2…vl-1vl得到的图，其中v1∈V(Cp)，vl∈V(Cq)。特别地，B(p，1，q)将Cp和Cq中的两个顶点粘合在一起得到的图。将3条两两内部不交的路Pp，Pq，Pr对应的端点粘合在一起构成的图记为P(p，q，r)。

图1 双圈图的基图

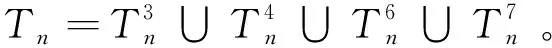
图2 三圈图的基图

当一条长为k的闭途径W经过图H每条边至少一次时，我们称图H能生成闭途径W。用记号∅G(H)表示G中H子图的个数，在不引起混淆情况下，用记号∅(H)表示。

下面给出在证明主要结论时用到的几个引理。

引理1[2]图G的第k阶谱矩等于G中长为k的闭途径的条数。

引理2[6]二部图只能生成长为偶数的闭途径。

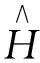
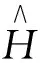
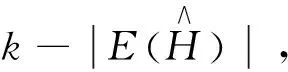
根据引理3，我们能得到下面推论。

推论1 令H是m圈图。若它能生成一条长为奇数k的闭途径W， 则|E(H)|≤k，等号成立当且仅当H是一个欧拉图。

推论2 若连通图G中恰有2个奇度点，且2个奇度点相邻，则G生成最短闭途径长度为|E(G)|+1。

证明设G中2个奇度点为u，v，令G′=G+uv，可知G′是欧拉图。根据推论1，G′生成最短闭途径长为|E(G′)|=|E(G)|+1。 由于G不是欧拉图，则G生成闭途径长度大于|E(G)|。故G生成最短闭途径长度为|E(G)|+1。

推论3 若连通图G中恰有4个奇度点u1，u2，u3，u4，且u1u2∉E(G)，u3u4∉E(G)，则G生成最短闭途径长度为|E(G)|+2。

证明令G′=G+u1u2+u3u4，可知G′是欧拉图。类似于推论2证明，G生成最短闭途径长度为|E(G)|+2。

2 本文的主要结果

定理1 能生成长为9的闭途径子图为C3，C5，C7，C9，K4，H1，…，H46，B(3，1，3)，B(3，1，4)，B(3，1，6)，B(3，2，6)，B(4，2，5)，B(4，3，5)，P(3，2，3)，P(3，2，4)，P(3，2，5)，P(4，2，5) (见图3)。

证明树子图、偶圈C4，C6，C8及分别以C4，C6，C8为基圈的单圈图，它们都是二部图。根据引理2，它们都不能生成长为9的闭途径。因此能生成长为9的闭途径子图一定含奇圈Ct，t∈{3，5，7，9}。K4是阶数最小三圈图，K5是阶数最小六圈图(其边数是10)，因此能生成长为9的闭途径子图一定是m圈图，m=1，2，3，4，5。下面分成5种情形来讨论。

情形1 生成长为9的闭途径子图是单圈图。

根据文献[6]中定理1.生成长为9的闭途径单圈子图是C3，C5，C7，C9，H1，...，H17。

情形2 生成长为9的闭途径子图是双圈图。

首先考虑双圈图不含悬挂树的情形。根据推论1，基图边数不超过9。

首先设双圈图为B(p，l，q)，这里q≥p≥3，l≥1。可知|E(B(p，l，q))|=p+q+l-1≥6，且p+q+l≤10。若(p，q)=(3，3)，则子图为B(3，1，3)，B(3，2，3)，B(3，3，3)，B(3，4，3)。若(p，q)=(3，4)，则子图为B(3，1，4)，B(3，2，4)，B(3，3，4)。若(p，q)=(3，5)， 则子图为B(3，1，5)，B(3，2，5)。若(p，q)=(3，6)， 则子图为B(3，1，6)。若(p，q)=(4，5)， 则子图为B(4，1，5)。根据推论1，可知B(3，4，3)，B(3，3，4)，B(3，2，5)都不能生成长为9的闭途径； 通过计算子图邻接矩阵9次幂的迹，可知B(3，2，3)，B(3，3，3)，B(3，1，5)生成长为9的闭途径条数都是0。

下面设双圈图为P(p，q，r)，这里r≥p≥q≥2。可知|E(P(p，q，r))|=p+q+r-3≥5，且p+q+r≤12。若(p，q，r)=(3，2，3)，则子图为P(3，2，3)；若(p，q，r)=(3，2，4)，则子图为P(3，2，4)；若(p，q，r)=(3，2，5)，则子图为P(3，2，5)；若(p，q，r)=(3，2，6)，则子图为P(3，2，6)。若(p，q，r)=(4，2，4)，则子图为P(4，2，4)；若(p，q，r)=(4，2，5)，则子图为P(4，2，5)；若(p，q，r)=(4，2，6)，则子图为P(4，2，6)。若(p，q，r)=(5，2，5)，则子图为P(5，2，5)。若(p，q，r)=(3，3，3)，则子图为P(3，3，3)；若(p，q，r)=(3，3，4)，则子图为P(3，3，4)；若(p，q，r)=(3，3，5)，则子图为P(3，3，5)；若(p，q，r)=(3，3，6)，则子图为P(3，3，6)。若(p，q，r)=(4，3，4)，则子图为P(4，3，4)；若(p，q，r)=(4，3，5)，则子图为P(4，3，5)。 根据推论1，可知P(4，2，6)，P(5，2，5)，P(3，3，6)，P(4，3，5)都不能生成长为9的闭途径；通过计算子图邻接矩阵9次幂的迹，可知P(4，2，4)，P(3，3，3)，P(3，3，5)，P(4，3，4)生成长为9的闭途径条数都是0。

下面考虑双圈图含悬挂树的情形。则基图的边数只能是5、6或7。

基图的边数为5。基图只能是P(3，2，3)。根据引理3， 它所有悬挂树边数和为1或2。若所有悬挂树边数和为1，此时图为H18，H19。若所有悬挂树边数和为2，由于P(3，2，3)不是欧拉图，根据引理3，此时图生成长为9的闭途径条数都是0。

基图的边数为6。基图为P(3，2，4)或B(3，1，3)。根据引理3， 它们所有悬挂树边数和为1。P(3，2，4)与一个悬挂树P2有3种不同粘合方式，依次得到图H20，H21，H22。B(3，1，3)与一个悬挂树P2有2种不同粘合方式，经计算粘合后图的邻接矩阵9次幂的迹都是0。

基图边数等于7。基图为B(3，2，3)，B(3，1，4)，P(3，3，4)，P(3，2，5)。根据引理3， 它们所有悬挂树边数和为1，且要生成长为9的闭途径，这些基图必须是欧拉图。只有B(3，1，4)是欧拉图，B(3，1，4)与一个悬挂树P2有4种不同粘合方式，依次得到图H23，H24，H25，H26。

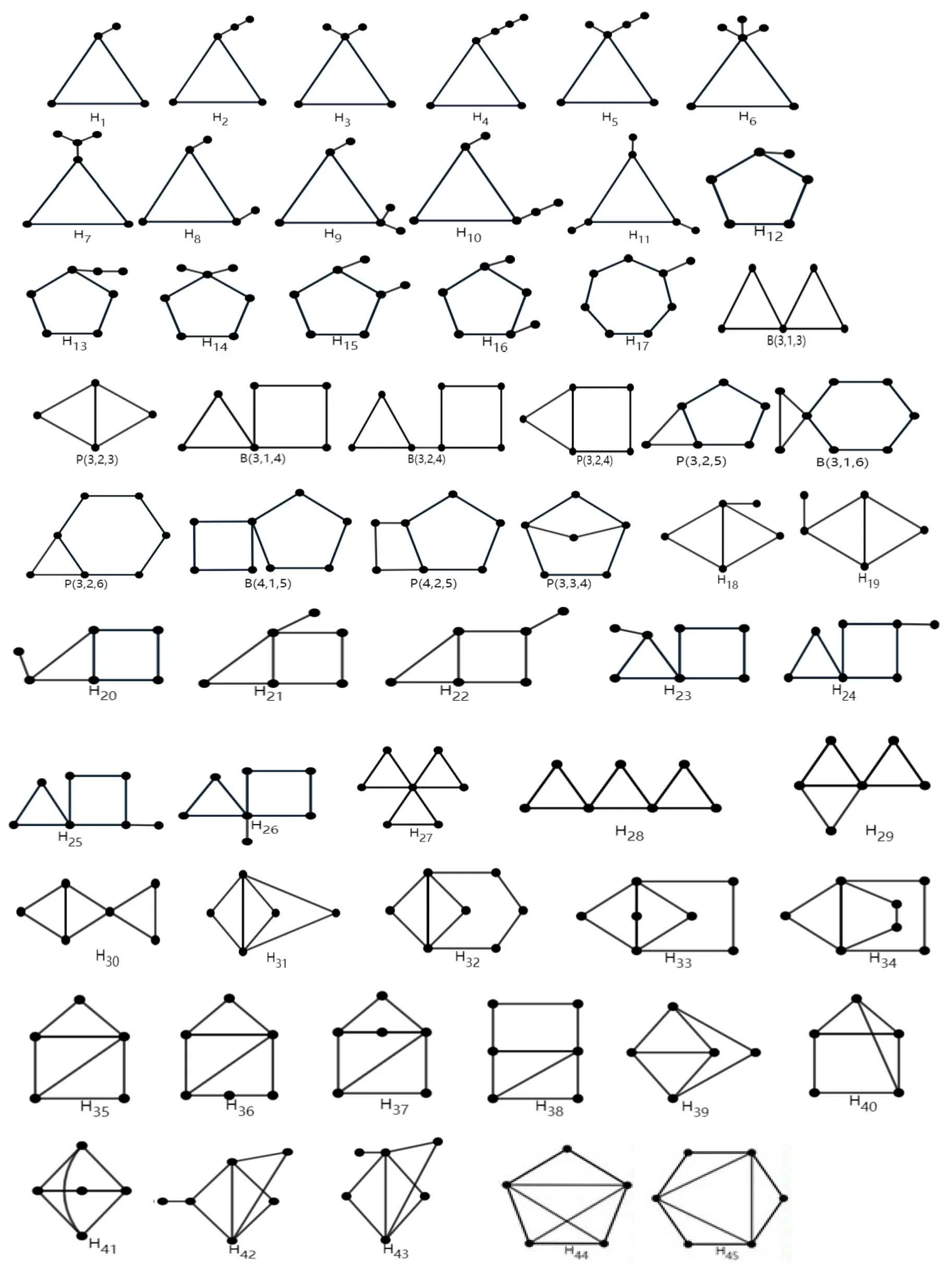
图3 所有能生成长为9的闭途径子图

情形3 生成长为9的闭途径子图是三圈图。

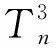
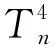
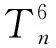
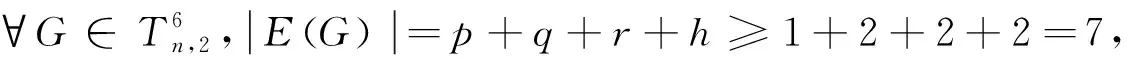
当{p，q，r}={1，2，2}，h=2时，图为H35；当{p，q，r}={1，2，2}，h=3时，图为H36；当{p，q，r}={2，2，2}，h=2时，图为H37；当{p，q，r}={1，2，3}，h=2时，图为H38。

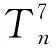
当{p，q，r}={1，2，2}，h=1时，图为K4；当{p，q，r}={1，2，2}，h=2时，图同构H39；当{p，q，r}={1，2，3}，h=1时，图为H40；当{p，q，r}={2，2，2}，h=1时，图为H41。

下面考虑三圈图含悬挂树的情形。则基图的边数只能是6或7。只有三圈图H31，H35，H39，H40，H41，K4符合条件基图。基图H31，根据引理3，所有悬挂树边数和恰为1。此时有1种不同方式粘悬挂树，得到图分别为H42，H43。H35，H39，H40，H41它们都不是欧拉图，根据引理3，以它们为基图的三圈图都不能生成长为9的闭途径。K4为基图的三圈图生成长为8，10，…的闭途径。

情形4 生成长为9的闭途径子图是四圈图。

当四圈图顶点数是5时，它的边数5+4-1=8即从K5中删除2条边。首先考虑这2条边是一个最大匹配。通过计算可知，该图生成0条长为9的闭途径。再考虑2条边不是最大匹配的情形，得到图H44。 当四圈图顶点数是6时，它的边数6+4-1=9。即从K6中删除6条边，根据引理3，这个图必须是欧拉图。可知图度序列为(4，4，4，2，2，2)。若有2个4度点不相邻，则它们与其余4个点都相邻，这时我们得到4个2度点，与度序列为(4，4，4，2，2，2)矛盾。因此3个4度点两两相邻。同理可证3个2度点是独立集合，此时图为H45。

情形5 生成长为9的闭途径子图是五圈图。

从K5中删除1条边，得到阶数最小五圈图。这个图度序列为(4，4，4，3，3)，可知它不是欧拉图。根据推论1，五圈图生成长为9的闭途径条数都是0。

综上所述，定理1证毕。

下面我们给出9阶谱矩的计算公式。首先我们设计了基于深度优先的搜索算法，利用该算法求解对于任意给定一个子图，由这个子图生成长为k的不同闭途径条数。这个算法为我们得到任意阶谱矩公式提供一种可能。算法代码，参看链接http：//qr61.cn/oK6EzX/q3CuHpU。

任意阶谱矩，只要能找到所有能生成阶闭途径的子图，用上述算法就能找到阶谱矩的公式。假设G中能生成长为k的闭途径所有子图为H1，…，Ht，我们能用算法确定每个子图生成长为k的比途径条数为Ci，则k阶谱矩

Sk(G)=c1φ(H1)+…+ctφ(Ht)，c1，…，ct∈Z+。

定理2 设G是n阶图，则

S9(G)=510φ(C3)+360φ(C5)+126φ(C7)+18φ(C9)+522φ(H1)+144φ(H2)+360φ(H3)+

18φ(H4)+36φ(H5)+108φ(H6)+36φ(H7)+180φ(H8)+36φ(H9)+18φ(H10)+18φ(H11)+144φ(H12)+18φ(H13)+36φ(H14)+18φ(H15)+18φ(H16)+18φ(H17)+288φ(H18)+216φ(H19)+

54φ(H20)+108φ(H21)+54φ(H22)+36φ(H23)+36φ(H24)+36φ(H25)+72φ(H26)+144φ(H27)+

72φ(H28)+216φ(H29)+108φ(H30)+1656φ(H31)+

108φ(H32)+108φ(H33)+108φ(H34)+324φ(H35)+

144φ(H36)+144φ(H37)+144φ(H38)+1872φ(K4)+

396φ(H39)+396φ(H40)+396φ(H41)+108φ(H42)+

216φ(H43)+3964φ(H44)+2884φ(H45)+ 288φ(B(3，1，3))+396φ(B(3，1，4))+36φ(B(3，1，6))+36φ(B(3，2，4))+72φ(P(3，2，6))+36φ(B(4，1，5))+144φ(B(4，3，5))+1584φ(P(3，2，3))+666φ(P(3，2，4))+72φ(P(3，2，5))+54φ(P(4，2，5))

证明由定理1知，生成长为9的闭途径子图C3，C5，C7，C9，K4，H1，…，H45，B(3，1，3)，B(3，1，4)，

B(3，1，6)，B(3，2，6)，B(4，2，5)，B(4，3，5)，P(3，2，3)，

P(3，2，4)，P(3，2，5)，P(4，2，5)。根据算法，我们得到9阶谱矩计算公式。故定理2成立。