ON CONTINUATION CRITERIA FOR THE FULLCOMPRESSIBLE NAVIER-STOKES EQUATIONS IN LORENTZ SPACES*
Yanqing WANG(王艳青)
Department of Mathematics and Information Science,Zhengzhou University of Light Industry,Zhengzhou 450002,China
E-mail :wangyanqing20056@gmail.com
Wei WEI (魏巍)+
Center for Nonlinear Studies,School of Mathematics,Northwest University,Xi 'an 710127,China E-mail: ww5998198@126.com
Gang WU(吴刚)
School of Mathematical Sciences,University of Chinese Academy of Sciences,Beijing 100049, China E-mail : wugang201 1 @ucas.ac.cn

1 Introduction
In this paper, we are concerned with the 3D full compressible Navier-Stokes equations

where ρ, u and θ stand for the flow density,velocity and the absolute temperature,respectively.The scalar function P represents the pressure, the state equation of which is determined by

and κ is a positive constant. µ and λ are the coefficients of viscosity, which are assumed to be constants, satisfying the following physical restrictions:

The initial conditions satisfy

It is clear that if the triplet(ρ(x,t),u(x,t),θ(x,t))solves system(1.1),then the triplet(ρλ,uλ,θλ)is also a solution of (1.1) for any λ ∈R+, where

The scaling of velocity u is the same as the incompressible Navier-Stokes system

In contrast with the pressure P = Rρθ in (1.1), the pressure Π in (1.6) is determined by ΔΠ = -divdiv(u ⊗u). The global well-posedness of the 3D Navier-Stokes equations (1.6) is an outstanding problem. It is well known that the solution u to (1.6) is regular on (0,T] if u satisfies
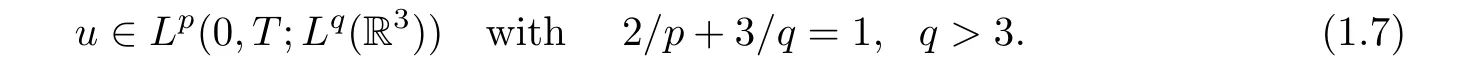
This is the so-called Serrin type regularity criteria for the incompressible Navier-Stokes system obtained in [27, 31]. Since the Lorentz spaces Lr,s(R3) (s ≥r) are larger than the Lebesgue spaces Lr(R3)and enjoy the same scaling as Lr(R3),Chen-Price[5],Sohr[32],and Kozono-Kim[20] presented an improvement of (1.7) by
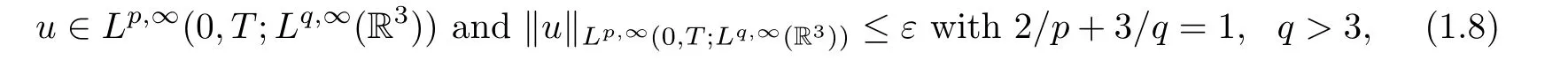
where ε is a positive constant. Alternative proofs of (1.8) are given in [3, 12, 35].
We turn our attention back to the full compressible fluid (1.1). The classical theory of compressible flow can be found in [10, 23]. Here, we are concerned with the regularity of local strong solutions to equations (1.1) established by Cho and Kim in [7] (for details, see Proposition 2.3 in Section 2). This type of strong solution allows the initial data to be in a vacuum. In the spirit of (1.7), many authors successfully extended Serrin type blow-up criteria(1.7) to the compressible flow (for example, [9, 15, 16, 18, 22, 22, 28, 29, 37, 38] and references therein). In particular, Huang, Li and Wang [15] proved the following sufficient condition for blow-up of solutions to (1.1):

It should be pointed out that the norms in (1.9)-(1.11) are scaling-invariant in the sense of(1.5). Inspired by (1.8), we shall prove the following result:
Theorem 1.1 Suppose that (ρ,u,θ) is the unique strong solution to (1.1). Then there exists a positive constant ε such that the solution (ρ,u,θ) can be extended beyond t = T provided that one of the following two conditions holds:
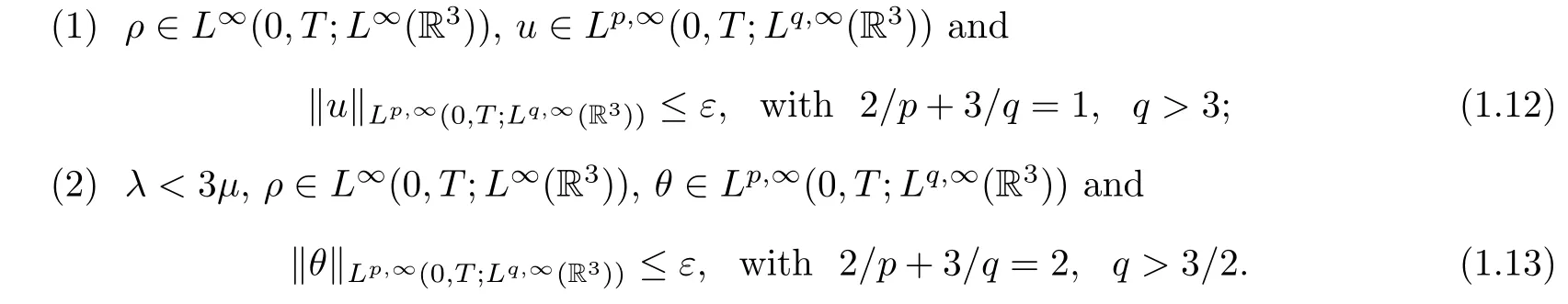
Remark 1.2 Theorem 1.1 generalizes both continuation criteria (1.10) and (1.11) to enable their space-time directions to be in Lorentz spaces.
Remark 1.3 Even if the results in this theorem reduce to the ones only involving space direction in Lorentz spaces, they are still new. In fact, it is known that the best blow-up criterion based on Lorentz spaces for compressible Navier-Stokes flows is
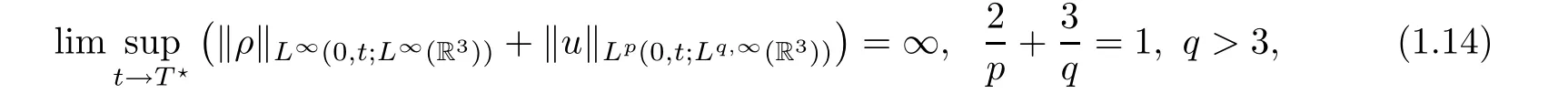
which was established for the isentropic compressible fluid by Xu and Zhang[38]. Hence, to the best of our knowledge,Theorem 1.1 is the first continuation criteria allowing the time direction to be in Lorentz spaces for the compressible fluid.
Remark 1.4 Since div u ∈L1(0,t;L∞(R3)) yields ρ ∈L∞(0,t;L∞(R3)), ρ ∈L∞(0,t;L∞(R3)) in this theorem can be replaced by div u ∈L1(0,t;L∞(R3)). Therefore, this theorem is an extension of (1.9).
The absolute continuity of the norm in Lorentz space Lp,l(0,T)(l <∞), together with Theorem 1.1, yields
Corollary 1.5 Suppose that (ρ,u,θ) is the unique strong solution to (1.1). Then the strong solution can be extended beyond t=T if ,for l <∞, one of the following two conditions holds:
(1) ρ ∈L∞(0,T;L∞(R3)), u ∈Lp,l(0,T;Lq,∞(R3)) with 2/p+3/q =1, q >3;
(2) λ <3µ,ρ ∈L∞(0,T;L∞(R3)),θ ∈Lp,l(0,T;Lq,∞(R3)) with 2/p+3/q=2, q >3/2.

Subsequently, we can apply the general Gronwall inequality in Lemma 2.1 and Lemma 2.2 to complete the proof. Finally, we would like to remark that it is still unknown whether (1.15)holds for the isentropic compressible Navier-Stokes system.
On the other hand, the authors of [34] recently obtained the following local regularity criteria in anisotropic Lebesgue spaces for suitable weak solutions to the incompressible Navier-Stokes system (1.6):

Here Q(̺):=B(̺)×(-̺2,0)and B(̺) denotes the ball of center 0 and radius ̺. This inspired us to consider the regularity of strong solutions to the compressible Navier-Stokes equations(1.1) in anisotropic Lebesgue spaces. Before formulating our result, we write

Remark 1.7 In contrast with(1.16),(1.18)requires the additional condition(1.17). This is due to the application of the Sobolev embedding theorem in anisotropic Lebesgue spaces.

The local existence of strong solutions to (1.20) in the sense of Proposition 2.4 was established by Choe and Kim in [8]. In addition, they showed that if T∗is the finite blow-up time, then

Our result concerning nonhomogeneous incompressible Navier-Stokes equations (1.20) is
Theorem 1.9 Assume that(ρ,u)is the unique strong solution to(1.20). Then there exists a positive constant ε such that the solution (ρ,u) can be extended beyond t=T provided that one of the following three conditions holds:
(1) u ∈Lp,∞(0,T;Lq,∞(R3)) and

Remark 1.11 Very recently, Wang [36] proved that (1.21) is also valid for nonhomogeneous incompressible Navier-Stokes equations with heat conducting. It is worth remarking that Theorem 1.9 also holds for this system. We leave the detail of this to interested readers.
The remaining part of this paper is organized as follows: in the next section,some materials involving Lorentz spaces and anisotropic Lebesgue spaces are listed. Several auxiliary lemmas are also given. Then, we recall the local well-posedness of equations (1.1) and (1.20). Section 3 is devoted to proving Theorem 1.1 and Theorem 1.6. In Section 4, we are concerned with lifespan of nonhomogeneous incompressible Navier-Stokes equations.
2 Preliminaries

It is well-known that
2.1 Some basic facts on Lorentz spaces
Next, we present some basic facts on Lorentz spaces. For p,q ∈[1,∞], we define

2.2 Some materials on anisotropic Lebesgue spaces

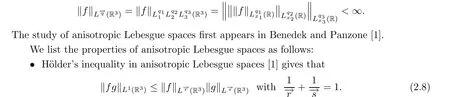
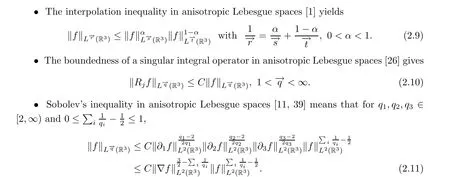
2.3 Auxiliary lemmas
The following powerful Gronwall lemma obtained by Bosia,Pata and Robinson in[3] helps us to prove Theorem 1.1:
Lemma 2.1 ([3]) Let φ be a measurable positive function defined on the interval [0,T].Suppose that there exists τ0>0 such that for all 0 <τ <τ0and a.e. t ∈[0,T], φ satisfies the inequality

Then φ is bounded on [0,T].
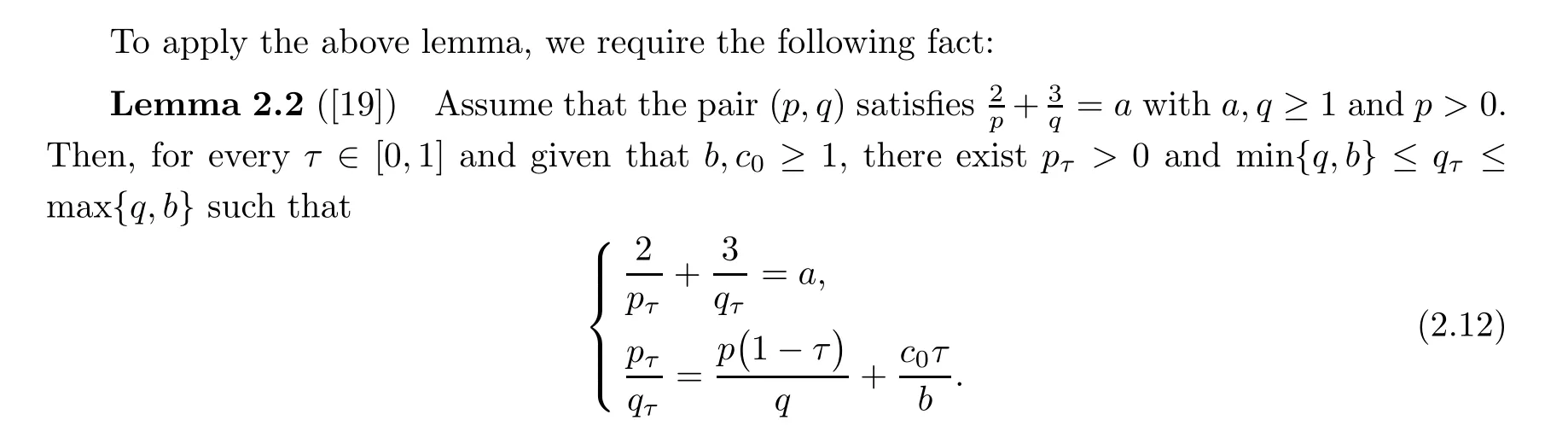
Finally,we recall the local well-posedness of strong solutions to the full compressible Navier-Stokes equations (1.1) and nonhomogeneous incompressible Navier-Stokes equations (1.20).Proposition 2.3 ([8]) Suppose that u0,θ0∈D1(R3)∩D2(R3) and
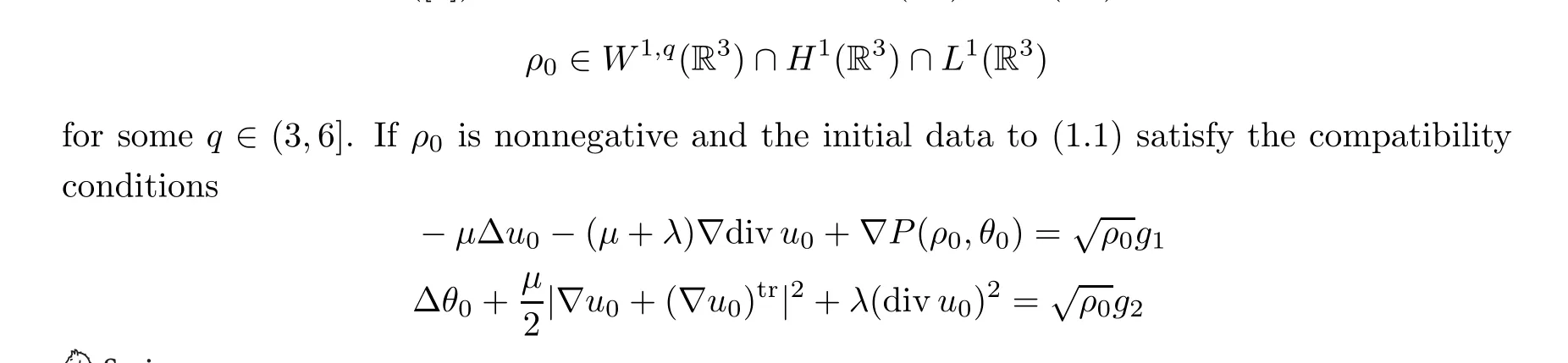
for vector fields g1,g2∈L2(R3), then there exist T ∈(0,∞) and a unique solution to (1.1)satisfying that
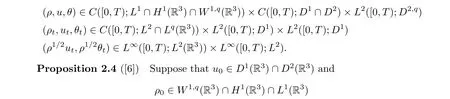
for some q ∈(3,6]. If ρ0is nonnegative and the initial data to (1.20) satisfy the compatibility condition

for vector field g ∈L2(R3),then there exist T ∈(0,∞)and a unique solution to(1.20)satisfying that

3 Full Compressible Navier-Stokes Equations
This section is devoted to proving Theorem 1.1.
Proof of (1) in Theorem 1.1 Multiplying (1.1)2by utand integrating over R3, we can write






In view of τ ∈[0,1], we know that δ ∈[0,1]. Finally, the proof is now based on applications of Lemma 2.1, (1.13) and (1.10). □
3.1 Continuation theorem in anisotropic Lebesgue spaces
Proof of(1)in Theorem 1.6 The interpolation inequality(2.9)in anisotropic Lebesgue spaces entails that

Combining this and Gronwall’s lemma, we are now able to complete the proof. □
4 Nonhomogeneous Incompressible Navier-Stokes Equations
We proceed with the nonhomogeneous incompressible Navier-Stokes equations in a fashion similar to the previous proof.
Proof of Theorem 1.9 Taking the L2inner product of the system with utand integrating by parts, we have that

Applying Lemma 2.1 to (4.2) and using (1.21), we complete the proof.
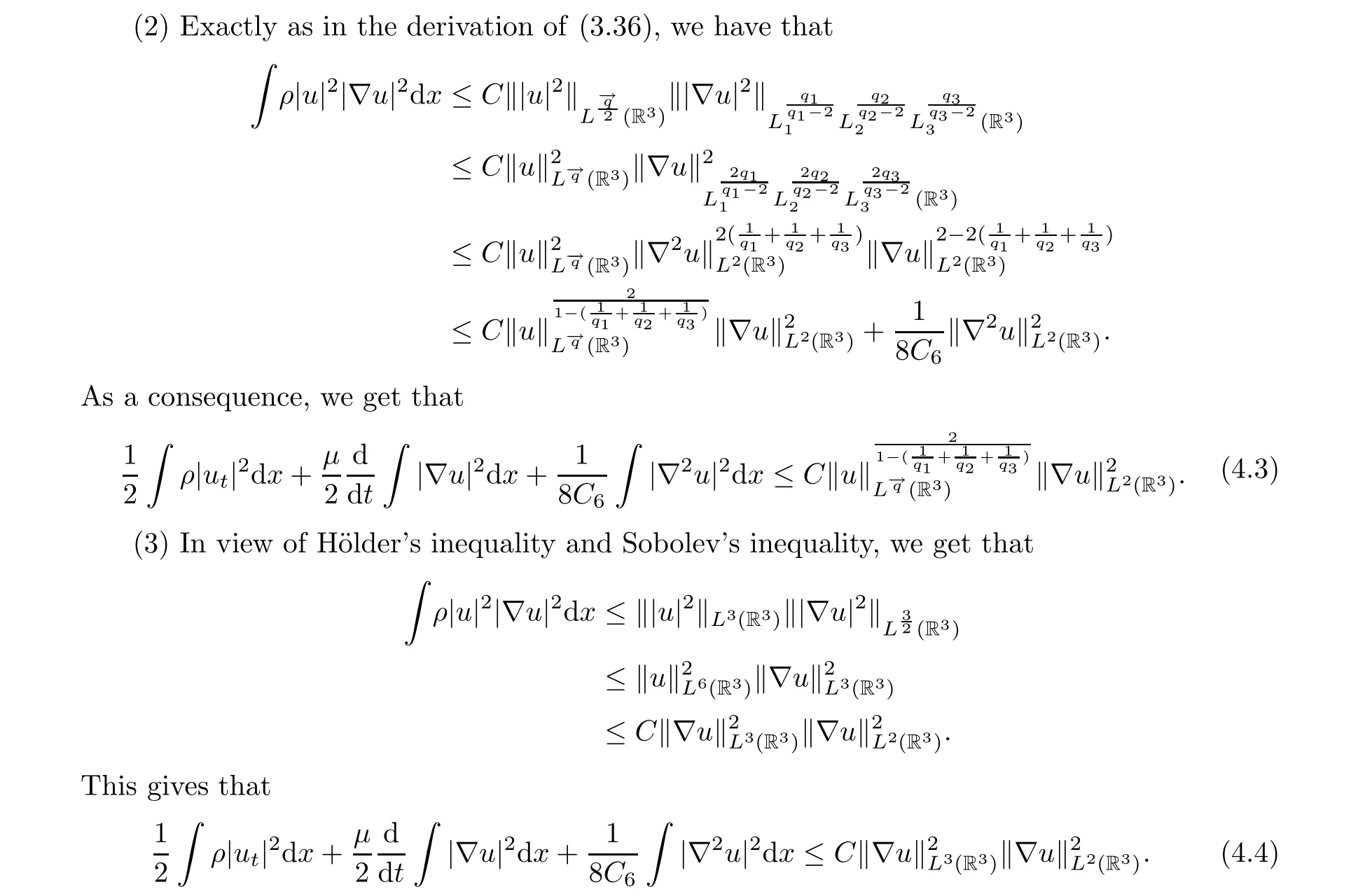
With (4.1), (4.3) and (4.4) in hand, and employing a classical Gronwall’s lemma, we complete the proof by (1.21).□
 Acta Mathematica Scientia(English Series)2022年2期
Acta Mathematica Scientia(English Series)2022年2期
- Acta Mathematica Scientia(English Series)的其它文章
- ARBITRARILY SMALL NODAL SOLUTIONS FOR PARAMETRIC ROBIN (p,q)-EQUATIONS PLUS AN INDEFINITE POTENTIAL∗
- SUP-ADDITIVE METRIC PRESSURE OF DIFFEOMORPHISMS*
- SHARP DISTORTION THEOREMS FOR A CLASSOF BIHOLOMORPHIC MAPPINGS IN SEVERAL COMPLEX VARIABLES*
- ON (a ,3)-METRICS OF CONSTANT FLAG CURVATURE*
- A NOTE ON MEASURE-THEORETICEQUICONTINUITY AND RIGIDITY*
- COMPLEX INTERPOLATION OF LP(C, HI)SPACES WITH RESPECT TO CULLEN-REGULAR*
