基于LASSO回归的 R-vine copula 模型构建及其在化工过程故障检测中的应用
邓红涛,贾 琼,李绍军,李 伟
(1.石河子大学,新疆 石河子 832000;2.华东理工大学 化工过程先进控制和优化技术教育部重点实验室,上海 200237)
过程安全和产品质量是目前化工过程被关注最多的两个问题,而过程监控是提高过程安全和产品质量的重要手段。随着集散控制和数据采集系统的广泛应用,工业过程采集数据的维度和数据量不断增加,导致基于经验知识和解析模型的方法在工业过程监控领域的研究受到了限制[1]。基于数据驱动的故障监控建模方法通过统计与分析过程数据来挖掘系统的特性,在描述未知机理模型和缺乏过程知识的复杂过程问题研究中备受学术和工业界关注。传统的数据分析方法有偏最小二乘法(PLS)[2]和主元分析法(PCA)[3],这两种方法适合分析具有线性、高斯分布特性数据。而处理非线性数据时常使用核方法来对这两种方法进行改进,进而形成核偏最小二乘(KPLS)法[4]、核主元分析(KPCA)法[5]等。这些方法主要是基于降维的方式将高维数据映射到低维特征空间,消除变量间的相关性,但在降维过程中数据携带信息量都会有一定的损失。
近年来,针对复杂数据的相关性研究中,copula理论得到了广泛的应用,将联合概率分布函数与边缘概率分布函数之间的相关性结构建立联系。由于多变量copula在构建维数较大的数据间的依赖性时缺乏灵活性,Joe[6]提出了pair-copula,该方法是将多变量copula用一系列的二元copula来表示,该方法在刻画高维数据的条件相关性、非对称性、尾部相关性等方面均体现出更大的灵活性,已经在金融、环境、工程等领域得到了广泛的应用。2015年Ren等[7]首先将vine copula函数引入到化工过程监控领域,提出了基于vine copula 相关性描述的多模态故障检测方法。Zheng等[8]利用D-vine copulas 混合模型实现了对复杂的工业过程监控。周南等[9]利用核密度估计法构建 R-vine copula 结构并用在工业过程故障检测中。由于二元copula函数类型众多,vine copula结构矩阵不固定,选取合适的vine copula结构矩阵和copula函数类型成为建模的关键环节。目前常规方法是利用贪婪算法计算所有可能矩阵结构下变量之间的相关关系,选择相关性最大的矩阵结构,然后根据赤池准则(AIC)选取copula函数类型和参数[10-12]。这种方法在处理高维的工业过程数据时,会出现计算量大、计算时间长的问题,其解也不能保证接近该高维组合优化问题的最优解。
笔者在构建R-vine copula模型时引入LASSO回归来统计变量之间的相关关系,根据变量间联系的强弱程度确定变量在R-vine矩阵中的位置,利用回归分析正则化路径选择R-vine copula矩阵结构。遵循R-vine矩阵构建规则和回归过程中惩罚力度调整变量在矩阵中的位置,确定R-vine结构矩阵模型,以获得一个与变量独立性有关的稀疏矩阵模型。该方法构建的矩阵结构独立于copula函数类型和参数,在处理高维度复杂工业过程数据时,利用稀疏模型和惩罚力度简化copula函数类型选择过程,缩短了建模时间,使统计建模具有更强的灵活性。该方法应用在TE(Tennessee Eastman)过程中表现出较好的检测效果。
1 R-vine copula 理论基础和LASSO回归
1959年Sklar第一次提出用copula函数分析复杂变量间的相关关系,将多维变量的联合分布函数用边缘分布函数和copula函数表示,但是这种copula函数面对高维数据时会出现参数过多而导致优化困难的问题[11]。1996年Joe[6]提出了vine copula结构。Vine copula结构分解具有较大的灵活性,分解策略较多[13-14]。2002年Bedford等[15]定义了R-vine copula 结构分解模型,相应的多元分布结构称为R-vine结构,可以更加灵活地表达变量之间的关系[16]。
1.1 构建R-vine结构矩阵规则
用树结构来表示vine结构,对于n维变量的R-vine分布,包含了n-1棵树,每棵树由节点和边组成。两个节点确定一条边,每条边用二元copula函数表示。由于vine copula结构分解模型多样,树型结构不唯一。为了更好地表示vine copula的结构,2013年Brechmann等[17]研究了一种R-vine copula结构模型,利用一个下三角矩阵M来表示R-vine分解模型,用矩阵M可以简单地表示出R-vine 结构中的树集T、节点集V和边集E。
对一个n维变量的vine copula结构,可以用一个n×n的下三角矩阵M表示,矩阵对角线元素m代表变量X={x1,x2,…,xn}中的xm。用mi,j表示第i行第j列矩阵元素,mi,j∈{1,2,…,n},i=(1,2,…,n),j=(1,2,…,i)。矩阵元素之间需要满足以下条件:
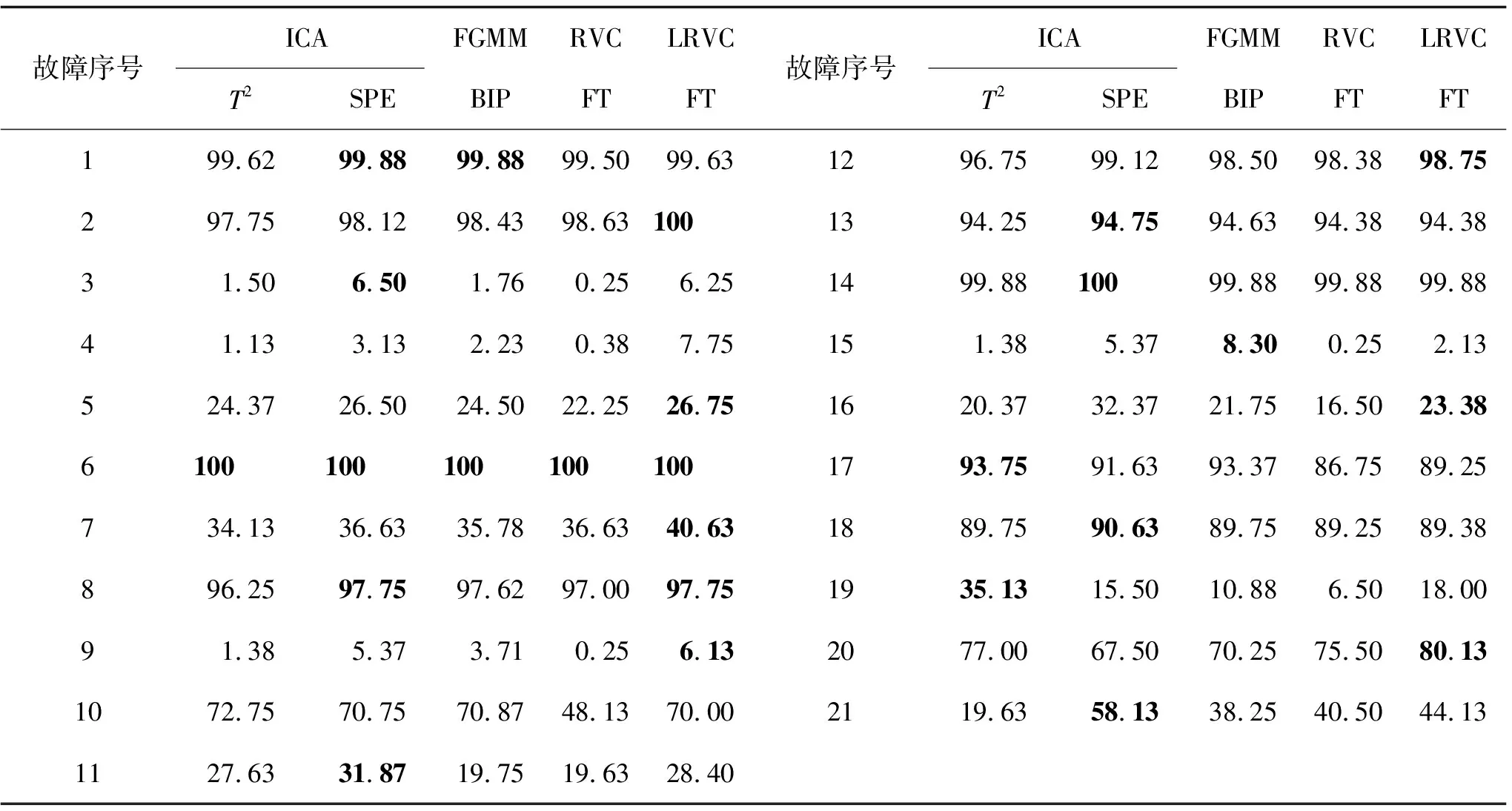
1){mj,j,…,mn,j}⊂{mi,i,…,mn,i},1≤i 2)mj,j∉{mi,i,…,mn,i},1≤j 3){mi,j,{mi+1,j,…,mn,j}}⊆{mk,k,{mw,k,…,mn,k}}。即如果矩阵元素集Q={mi,j,{mi+1,j,…,mn,j}},j=(1,2…,n-2),i=(j+1,…,n),那么一定存在包含或等于Q的元素集{mk,k,{mw,k,…,mn,k}},j 设满足以上规则的矩阵M中第i行第j列元素m集合为W。 根据以上条件可以发现矩阵中元素位置是互相约束的,如图1所示矩阵M,组成第2列的变量{4,2,1,3}包含在第1列{5,2,1,3,4}中;第2列对角线元素{4}不会出现在第3、4、5列中;第1列画圈元素组成元素集Q={3,4},那么至少第2列中存在包含Q的元素集{4,1,3}。 图1 5维变量的R-vine矩阵M 假设画圈元素m4,1为O,O和第1列中行数大于4的元素组成元素集Q={O,4}。列数大于1、行数大于等于4的元素和对角线元素(带上横线元素)组成的元素个数大于等于Q的元素集{4,1,3}、{3,2,1}、{2,1},这些元素集中包含元素4的只有{4,1,3},根据条件3可知画圈位置的元素O只能在变量集W={3,1}中选取。 利用R-vine的矩阵结构,不需要画树结构就可以快捷地表示出多维变量的联合密度函数[18]。矩阵元素mi,j和第j列元素可以表示树Tn-i+1的第i-j+1个二元copula函数cj(e),k(e)|D(e)(Fj|D(xj(e)|xD(e)),Fk|D(xk(e)|xD(e))),其中j(e)=mj,j,k(e)=mi,j,D(e)={mi+1,j,…,mn,j},i=(2,3,…,n),j=(1,2,…,i-1),F为条件累计分布函数。 n维变量的联合概率密度P可以表示为边缘概率密度f(xi)与copula密度函数c的乘积形式: (1) 式中:fi(xi)为第i个变量xi的边缘概率密度函数,cmj,j,mi,j|mi+1,j,…,mn,j为二元copula函数,F(xmj,j|xmi+1,j:mn,j)为xmj,j的条件累计分布函数。 图1所示矩阵M为R-vine结构矩阵,矩阵中元素m的值1-5代表变量X={X1,X2,X3,X4,X5}。矩阵M中画圈元素m4,1=3,对应二元copula为:c3,5|4,变量m1,1条件密度可以用第1列所有元素的二元copula函数之积和对角线元素的边缘密度表示: f(x5|x1x2x3x4)=f(x5)c4,5c3,5|4c1,5|3,4c2,5|1,3,4。 (2) 联合概率密度为: f(x1,x2,x3,x4,x5)=f(x1)f(x2|x1)×f(x3|x1x2)f(x4|x1x2x3)f(x5|x1x2x3x4)。 (3) 根据矩阵M求5维变量联合概率密度,即: f(x1,x2,x3,x4,x5)=f(x1)f(x2)f(x3)f(x4)f(x5)×c1,2c1,3c3,4c4,5c2,3|1c1,4|3c3,5|4c2,4|1,3c1,5|3,4c2,5|1,3,4。 (4) 在满足矩阵规则的前提下构造合理的R-vine结构矩阵M是构建R-vine copula模型的关键[19]。目前常用贪婪算法构建R-vine树的结构矩阵,计算树节点之间的相关性,按照最强相依性原则遍历所有可能的矩阵结构,寻找最大相关系数之和以构建R-vine结构矩阵,并在整个结构选择过程中迭代拟合copula函数及其参数。此方法计算时间长,计算量大,构建的模型结构复杂,容易出现过拟合现象。 线性回归表示变量间相互依赖的定量关系,变量x={x1,x2,…,xn}回归函数如下: (5) 式中φm为变量xm的回归系数。 LASSO回归是一种数据降维方法,善于处理变量的筛选。1996年Tibshirani[20]首次在普通线性回归模型中添加了惩罚项,通过改变惩罚项将一些作用比较小的变量线性系数压缩,最终变为零,从而获得稀疏解。这种基于惩罚方法对样本数据进行变量选择,防止了数据过拟合,不但可以用于线性关系,也可以用于非线性关系。回归损失函数公式如下: (6) 式中:hφ(x(t))是根据式(5)计算预测第t个样本的值,因变量y为真实样本值,q为样本个数,t=(1,2,…,q),λ为正则化参数,r为参数个数,k=(1,2,…,r)。随着λ增大,各变量的系数逐渐趋于零。 将LASSO回归算法用于构建R-vine结构矩阵,提出一种新的构建R-vine结构矩阵的方法[21]。如构建n维变量X={X1,X2,…,Xn}的R-vine结构矩阵M。 首先确定R-vine结构矩阵M中的对角线元素。将变量带入式(7),按照式(6)利用交叉验证方法确定过程变量xi(i=1,2,…,n)的LASSO回归方程。 (7) 式中:m=1,2,…,n,z=1,2,…,n,且m≠z。根据式(8)统计n个回归方程中变量xm的回归系数φm,z非零的个数uz,按照uz的升序将变量xm设为R-vine结构矩阵M的对角线元素,当出现次数相同时按照回归系数的和排序。 (8) 如图1所示,矩阵M确定对角线元素时,存在u5≤u4≤u3≤u2≤u1,那么对角线元素为{5,4,3,2,1}。 接下来按照从右往左、从下至上的顺序确定矩阵中的其他元素。如确定矩阵M中的变量mi,j,以矩阵对角线元素xmj,j为因变量y,根据R-vine结构矩阵构建规则,以满足元素集W的元素为自变量,带入式(5),根据式(9)利用最小回归角方法选择变量,当回归系数依次置为零时,惩罚项最大的变量即为mi,j。 (9) 式中:W为根据R-vine矩阵规则确定的此处可放置的变量集合,l是属于集合W的元素。 确定图1中矩阵M第5行第4列的元素,根据R-vine矩阵规则可知m5,4=1,然后按照从右往左、从下至上的顺序依次确定m5,3、m5,2、m5,1、m4,3、m4,2、m4,1、m3,2、m3,1、m2,1。确定画圈元素m4,1时,根据构建R-vine结构矩阵规则推出可用变量W={1,3},则以m1,1为自变量y,以m4,2和m5,5为因变量,按照式(5)利用LASSO回归计算回归系数,按照式(9)利用最小回归角方法调整惩罚项。当φ1=0时λ=λ1;φ3=0时λ=λ3。因为存在λ1<λ3,那么m4,1=3。 本研究中利用LASSO回归过程反映变量之间关系的特点,按照变量回归系数归零速度和惩罚项大小确定R-vine结构矩阵M,利用正常样本数据根据赤池准则确定R-vine copula模型中参数,构建模型,利用阈值法进行在线故障检测(如图2所示)。 图2 LRVC过程监控方法示意图 1)获得正常操作过程的训练样本集,按照第2节方法构建R-vine矩阵M。 2)根据R-vine矩阵M确定copula对和参数,构建R-vine copula模型。合适的copula对能够精确地描述变量数据间的相关关系。采用基于似然函数的赤池信息准则[23]选取最合适copula对类型。赤池准则是权衡被估计模型复杂度和拟合优越性的一种标准,其定义如下: (10) 3)确定检测阈值T。 计算样本点的联合概率密度,利用分位数法[7]求对应的联合概率密度中阈值T。该方法根据高密度区域与密度分位数理论构建广义贝叶斯推断概率指标(GLP),阈值T选取99%的控制限,监测时对比静态密度分位数表确定监测状态。 1)利用模型计算监测数据联合概率密度函数。 2)以阈值T为界限,小于阈值则为故障数据。 Eastman 公司依照实际的化工反应过程开发了TE测试平台,仿真数据具有非线性、时变和强耦合性等特征,能很好地模拟复杂工业过程,被广泛应用于控制、优化、过程监控与故障诊断的研究。TE数据集由训练集和测试集构成,数据集包含了正常状态数据和21种故障状态数据,每个样本都有52个观测变量,其中连续变量22个,操纵变量12个和成分变量19个。本研究所用数据可从http:∥web.mit.edu/braatzgroup/links.html下载,在离线状态下选取了正常工况下样本52个变量中的22个连续的过程变量构建R-vine copula模型,采用960个正常样本点来建立模型,每种故障状态的测试数据也选用960个样本点进行测试,对21个故障数据进行监测。将本研究中提出的方法LRVC与独立成分分析(ICA)、高斯混合模型(FGMM)、R-vine copula(RVC)等算法计算TE过程故障检测率进行比较,结果见表1,其中T2和SPE是ICA故障检测的统计指标,T2指标衡量样本向量在主元空间的变化,SPE指标衡量样本向量在残差空间的投影的变化,BIP是贝叶斯推理的后验概率(BIP)指标,FT指利用RVC模型和LRVC模型下的广义贝叶斯推断概率指标。表中粗体表示检测效果最好的值。 表1 TE过程故障检测率对比表 可以看出利用LASSO回归构建的R-vine模型监测结果优于贪婪算法构建R-vine矩阵建模,与FGMM、ICA方法[23-24]比较具有较高的检测率。LRVC模型的故障检测率都略高于利用贪婪算法构建矩阵的模型检测率,在故障2、4~9、12、16、20中都表现出较好的检测效果,其他故障的检测效果和其他方法相差不多。LRVC模型有13类故障的检测率都高于FGMM方法的检测结果,相比于ICA检测方法在故障2、4、5、7、9、12、20中都表现较好检测率。 TE过程中数据具有非高斯态的特性,FGMM方法是基于马氏距离判断数据是否异常,反映数据的非高斯特性能力较差;ICA方法在数据变换和特征提取的过程中会造成部分信息的损失。而LRVC方法利用LASSO回归建立R-vine矩阵构建模型,全面挖掘出数据变量之间的信息,在刻画非高斯、非线性方面有显著的优势,提高了故障检测的性能。图3为LRVC方法对故障8和故障12的监控图,横坐标为对联合概率密度P取对数。 图3 TE过程故障 8、12的LRVC监控图 醋酸脱水过程控制系统包括4个进料和90级塔板,用于建模的300组测试数据和500组训练数据来自分布式控制系统(DCS),包括温度、流量、压力等连续的21个监测变量。表2为核主元分析KPCA、FGMM、和LRVC 3种方法的检测率(fault detection rate,FDR)和误报率(false positive rate,FPR),可见LRVC方法在醋酸脱水过程监测中表现较好。 表2 醋酸脱水过程检测率和误报率 提出了一种基于LASSO回归构建 R-vine copula 模型的化工过程故障检测方法LRVC,与传统方法相比具有较好的检测效果。LRVC模型利用LASSO回归过程反映变量之间相关性的特性,依据回归过程惩罚力度构建R-vine矩阵,采用赤池准则进行copula类型选择构建R-vine copula模型。模型中利用LASSO回归统计多元变量相关性构建R-vine矩阵更能体现vine copula结构分解特性,适合高维变量数据分析。基于LRVC模型的过程故障检测方法充分利用了copula函数可以反映变量之间非高斯、非线性的特性,在不降维的情况下直接描述变量之间关系,具有更好的解释能力和适应性。此方法简化了构建R-vine矩阵过程,在超高维变量的建模过程中可以直接利用矩阵进行copula函数的选择,节省了建模时间。该方法在TE过程以及醋酸脱水过程中的应用表明其在工业过程故障检测中具有应用前景。
1.2 利用矩阵M表示联合密度函数
1.3 LASSO回归
2 利用LASSO回归构建R-vine矩阵
3 基于LASSO构建R-vine copula模型的故障检测方法
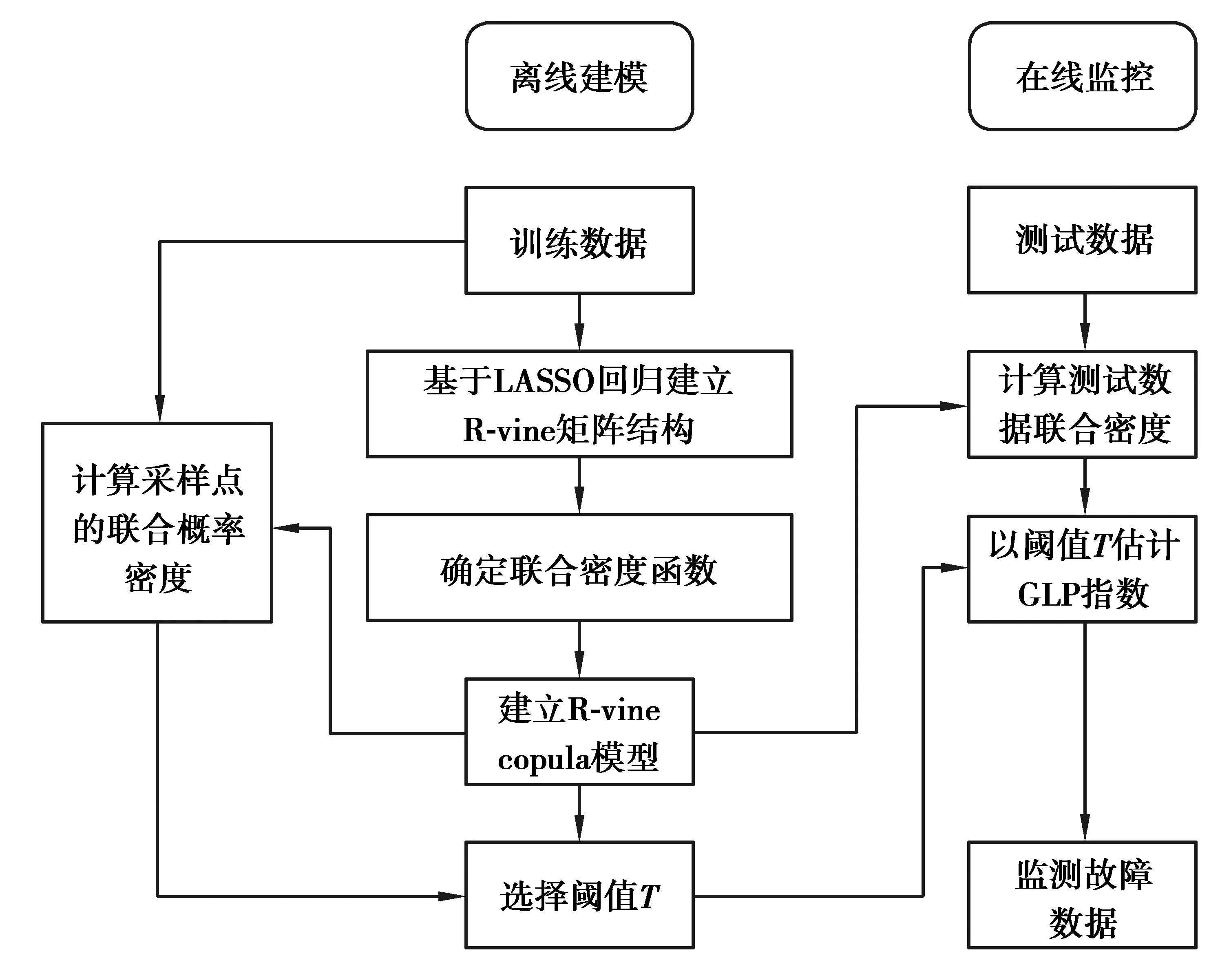
3.1 离线建模

3.2 在线监控
4 应用分析
4.1 TE过程

4.2 醋酸脱水过程

5 结 论

