等时圆
——求解物体沿光滑斜面滑行问题中的桥梁

王伟民，牟银勇

1.安徽省太和县宫集镇中心学校，安徽 太和 236652

2.重庆市育才中学，重庆 400050

1 引言

物体沿倾斜的光滑细杆从顶端由静止状态自由滑行至底端所用时间的长短，跟细杆的倾角和细杆的长短都有关系，细杆越长，细杆的倾角越小，物体沿细杆由顶端自由滑行至底端所用的时间就越长。可以证明，如果几根光滑细杆的顶端重合，底端位于以顶端为竖直直径一个端点的同一个圆周上，那么，物体沿各细杆由顶端自由滑行至底端所用的时间相等，都等于物体做自由落体运动下落与圆直径相等的距离所用的时间。这个圆被称为与光滑细杆对应的等时圆，该规律即为等时圆的性质。

2 等时圆性质的论证

如图1所示，设光滑细杆AB的倾角为α，AB两点位于竖直平面内⊙O的圆周上，且AC是⊙O的竖直直径，⊙O的半径为R。下面推导滑环P沿AB由顶端A自由滑行至底端B需要的时间跟⊙O半径R及其他各相关物理量之间的关系式。

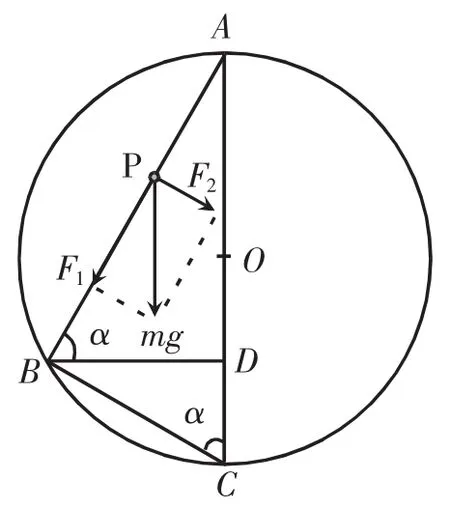
图1 等时圆的物理和几何关系

根据已知条件并结合圆的几何性质可知，细杆AB的长度为AB=2Rsinα，将滑环重力mg分解为沿细杆方向的力F1和垂直于细杆方向的力F2。显然，F1=mgsinα，所以，滑环沿细杆方向的加速度为a=gsinα。因此，滑环由A端自由滑行至B端需要的时间为

这一时间恰好为物体做自由落体运动下降与圆的直径2R相等的高度需要的时间，问题得证。

3 等时圆性质的应用

物体沿光滑细杆或光滑斜面由静止释放自由滑行问题中，给出合适的条件，可以求解相关的未知物理量。对于涉及这方面内容的题目，在求解问题的过程中，如果增添合适的辅助等时圆，往往可以使问题的解决变得简单明了。下面以两个具体例子进行说明。

3.1 求解两个滑动物体的相对滑动速度

例题1如图2所示，竖直平面内足够长的光滑细杆PA和PB的上端点重合，它们与水平面MN的夹角分别为α和。两个小环分别套在两根细杆上，由P点静止释放，求经时间t后两小环相对速度的大小。

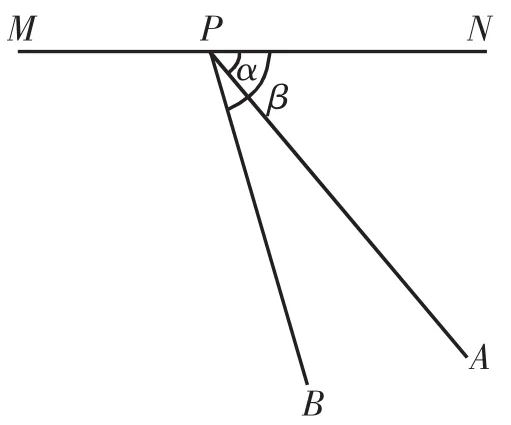
图2 小环在竖直面内的细杆上运动

3.1.1 采用矢量运算的方法进行求解

这道题的解法比较多，我们先采用矢量运算的方法进行求解。

解析如图3所示，设时间t后，套在两根光滑细杆的两个小环分别沿两根细杆下滑至C点和D点位置，设此时它们的速度分别为vC和vD，则两个速度的大小分别为

图3 例题1分析图

vC=gtsinα，vD=gtsinβ

将这两个速度分别在水平方向和竖直方向分解，并写成矢量式，有

以细杆PA上的小环为参照物，则细杆PB上小环的相对运动速度为

细胞持续缺氧,重要脏器的功能发生障碍,乳酸的清除能力降低,这是导致高乳酸血症的重要原因之一[5]。乳酸是体内葡萄糖无氧酵解的产物。患者的乳酸持续时间和血乳酸水平是判断病情严重程度和预后的重要指标。单纯监测某一时刻的血乳酸浓度,不能作为准确判断治疗措施的效果,不能准确反映机体的状态及疾病的发展情况。研究[6]表明:血乳酸水平越高,病死率越高;如血乳酸低于1.4mmol/L,则病死率为0;如血乳酸超过13 mmol/L,则病死率接近100%。因此,观察血乳酸水平的动态变化,计算血乳酸的清除率,可准确反映出病情演变的趋势。

所以，以细杆PA上的小环为参照物，细杆PB上的小环相对运动速度的大小为

用同样的方法可以求得两个滑杆上的小环相对加速度大小为a=gsin（β-α）。

可以发现，上面的推理过程非常麻烦，求解过程的大部分内容是数学中的三角变换，已经把物理问题的“物理味道”给冲淡了。那么，我们可否另辟蹊径，寻找相对简便的方法对问题进行求解呢？考虑到等时圆中，物体沿倾角不同的光滑斜面（或光滑细杆）从某个竖直圆周的最顶端（即该圆竖直直径的上端点）静止释放，滑行到斜面（或细杆）与圆周的另一个交点所用的时间相等，所以，我们可以尝试用增添辅助等时圆的方法来对问题进行求解。

3.1.2 采用添加辅助等时圆的方法进行求解

如图4所示，过P作竖直线PH，两个小环在光滑细杆PA和PB上同时由P点静止释放。假设在某时刻沿细杆PA向下自由滑行的小环到达C点，作圆心在PH上，并且过PC两点的圆⊙O（作PC的中垂线，与PH的交点便是需要作的圆的圆心位置）。显然，在指定时刻，满足条件的圆不仅存在，而且是唯一的。设⊙O交PB于点D，由等时圆的性质可知，当沿细杆PA自由滑行的小环到达C点时，沿细杆PB自由滑行的小环刚好到达D点。因为MN是⊙O的切线，由弦切角的性质可知，∠CDP=∠APN=α。如图5所示，如果在射线PH上O点下方任取一点I，以I为圆心、IP为半径作圆，⊙I分别交PA、PB于E点和F点，由等时圆的性质可知，在滑杆PA上滑行的小环滑行至E点时，在滑杆PB上滑行的小环恰好滑行至F点，易知，△PCD∽△PEF。这说明两个小环在由P点静止释放开始自由滑行时计时，之后的任意时刻，它们所在的两点与起始位置点组成的三角形都是相似的。所以，在任意时刻，两小环在空间内的相对方位始终保持不变。由初速度为零的匀变速直线运公式和v=at可知，运动时间一定时，从初始位置计时，运动一定时间后某时刻物体的位移正比于物体的加速度，这时刻物体的速度也正比于物体的加速度。在图5中，由正弦定理可知所以。因此，从开始滑行时计时，经过时间t之后，在滑杆PA上滑行小环的滑行速度为vC=gtsinα。故经时间t后两根滑杆上的两个小环的相对滑行速度为

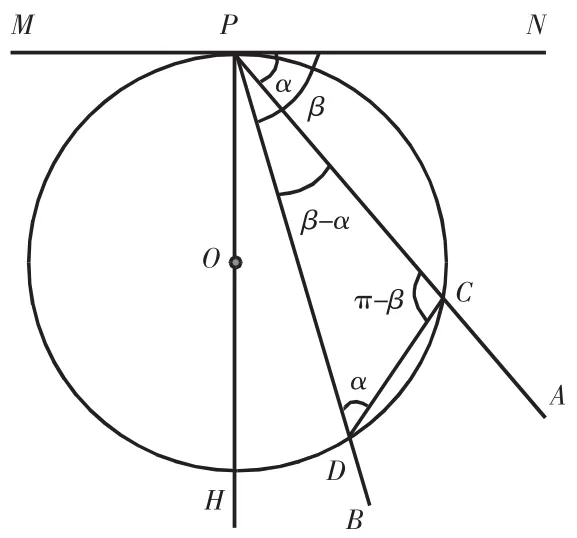
图4 利用等时圆分析小环的运动

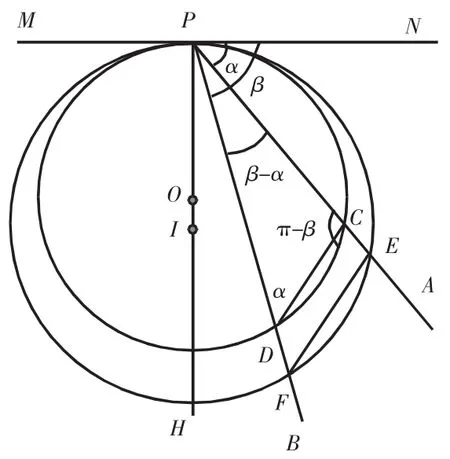
图5 利用等时圆分析小环运动的速度

3.2 求解物体滑行的最短时间

例题2如图6所示，OA是坡比为3：4的斜坡，在斜坡底端O点正上方45 m处有一固定点P。一光滑细杆PC底端C放在斜面上且可自由调节位置，细杆始终过点P，套在细杆上的小环由P点静止释放，试求小环沿细杆滑行至斜面的最短时间？（取g=10 m/s2）

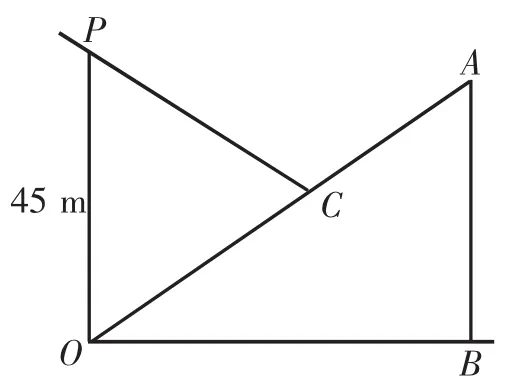
图6 小环在斜坡上的杆上滑行

分析如图7所示，作圆心在OP上、经过点P并且与OA相切的圆⊙I，交PC于D。易知，这样的圆不仅存在，而且该圆的位置和大小都是唯一确定的。设⊙I与斜面的切点为E，由图可知，斜面OA上的所有点，除了切点E在⊙I的圆上之外，其余各点全部在⊙I的外面。连接PE，若将PE、PC视为光滑细杆的话，由等时圆的性质可知，套在两根光滑细杆上的两个小环从P点同时静止释放，在细杆PC上的小环滑行至D点所用的时间与在细杆PE上的小环滑行至切点E所用的时间相等。因此，小环沿过切点E的细杆由P滑行至斜面所用的时间最短。

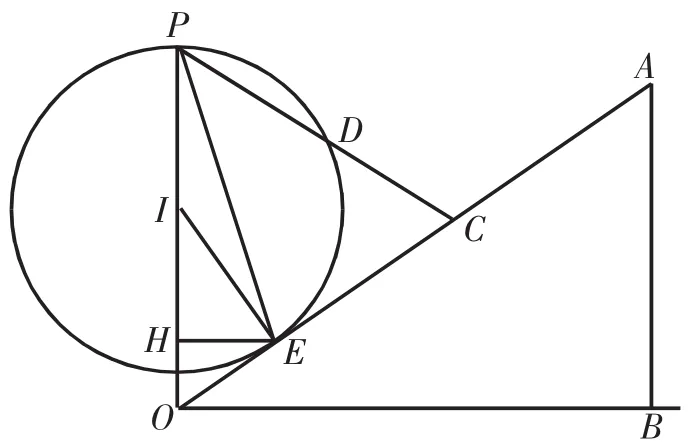
图7 利用等时圆分析小环的运动

解析作EH⊥OP，垂足为H。因为OA与⊙I相切，所以IE⊥OA，所以△IHE∽△IEO∽△EHO∽△OBA，所以这些相似直角三角形较短直角边与较长直角边之比都等于斜坡的坡比3：4。设⊙I的半径为r，则，所以

因此，小环在光滑细杆PE上向下自由滑行的加速度大小为

小环沿光滑细杆由P点滑行至斜面需要的最短时间为

对于例题2给出的问题，也可以采用建立合适坐标系的方式用解析法进行求解。对于经过P点的任意向右下方倾斜的光滑细杆，建立小环在细杆上由P点静止释放沿细杆自由滑行到斜面过程中，需要的时间与相关参数间的函数关系式，利用求导确定驻点的方法亦可确定问题的答案，但这样的方法解题过程将会非常复杂，而且学生不易理解。

4 两个例题对应问题的解法总结

可以发现，例题1和例题2分别对应两个不同类型的运动学问题。前者是两个滑环分别沿两个不同倾角光滑细杆同时开始滑行经历确定的时间后，求解它们的相对滑动速度；后者是求解滑环沿不同倾角光滑细杆从斜面上方的某个固定点滑行至斜面上的最短时间。虽然都采用了添加辅助等时圆的方法，但解决具体问题的方法也存在差别。前者借助等时圆构造相似三角形，利用相似三角形的性质并结合匀变速直线运动的运动学公式中速度与位移的定量关系进行解析；后者则借助等时圆，根据圆切线上的各点中唯有切点到圆上最高点的距离最短，并结合等时圆的性质进行求解。

当然，对于这两个问题，如果物理情境适当改变，则对应的物理问题也会发生相应变化，在条件允许的情况下，我们依然可以采用增添辅助等时圆的方法进行求解。比如，例题2对应的物理情境，我们可以将坡比已知的斜面改换为其他曲面，例如改换为圆心、半径确定（半径大于图7中⊙I的半径）的圆柱体的侧面，那么，我们仍然可以采用与例题2解法类似的方法进行求解，而且相比于其他方法解题过程更为简洁。

5 结语

等时圆，恰如一座桥梁，在运动学板块物体沿光滑斜面（或光滑细杆）由静止释放自由滑行问题中，将等时圆这座“桥梁”恰到好处地架设于已知条件和所求的问题之间，利用等时圆的性质，并结合圆的有关几何性质，有时可以起到化腐朽为神奇的作用，使常规解法下繁杂晦涩的求解过程变得简洁明快。