衔接：搭建从小学算式通往初中方程的“桥”

万涛 倪军

【摘要】中小学数学内容的衔接是构建整个义务教育体系的重要环节，是贯通核心素养表现的重要方式，是贯彻立德树人的重要途徑．由于中小学数学的学段目标不同、要求不同、衔接不清晰等原因，导致部分学生进入初中后，在数学学习中出现对知识不能自然过渡、对知识困惑不理解、对数学学习不适应等现象，因此，探索中小学数学内容之间的关联，搭建中小学数学之间的“桥”，把有关联的知识进行衔接，将中小学的核心素养贯通起来显得至关重要．

【关键词】衔接；教学模式；一致性；核心素养

1课标分析

在《义务教育数学课程标准（2011年版）》实施中，产生中小学数学内容的连续性不明确，程度衔接不清晰等问题，如“鸡兔同笼”和“三角形内角和”等．在《义务教育数学课程标准（2022年版）》（以下简称《课标（2022年版）》）中提到：“核心素养具有整体性、一致性和阶段性，在不同学段具有不同表现．小学阶段侧重对经验的感悟，初中阶段侧重对概念的理解．”[1]学段不同，学段目标的要求也不同，学段主题也有所不同．小学阶段主要以数与运算为主，初中阶段主要以数与式、方程、不等式和函数为主．教学要依据学生从小学到初中在认知、情感、社会性等方面的发展，合理安排不同学段内容，体现学习目标的连续性和进阶性，《课标（2022年版）》极其关注不同学段之间的衔接与联系.

2学情分析

部分学生在小学数学成绩很好，可是当进入初中后，一方面，学段目标变了，学习环境变了，教师的教学方式变了，这使部分小学毕业生未能很快适应初中的学习环境和教学方式，以至于部分学生在数学的学习上出现了明显不适应；另一方面，由于小学数学和初中数学在内容和目标上存在衔接不清晰、不明确之处[2]．一些初中教师对小学的数学内容、学段目标和知识体系不熟悉，对小学和初中的数学知识不能有效进行衔接，以至于部分学生不太适应初中数学的学习，这说明中小学的数学教材和教学都存在衔接不清晰的现象，所以，初中数学教师在教学时要关注学生在小学学习数学的学情，对中小学的教学内容进行有效衔接，帮助学生实现由“初等数学思维”向“高层次数学思维”的过渡，在促进中小学数学教学内容有效衔接的同时，构建中小学数学知识之间的连续性、整体性和一致性，培养学生应有的数学核心素养，使学生在数学学习中，体验数学知识产生的自然性、合理性和必要性，使学生经历知识发生和发展的过程，明白知识的来龙去脉，有效提升学生学习数学的兴趣，建立学生学好数学的信心，养成良好的学习习惯，形成质疑问难、自我反思和勇于探索的科学精神.

3备课思考

古代著名的数学趣题——“鸡兔同笼”：今有雉兔同笼，上有三十五头，下有九十四足，问雉兔各几何？意思是有若干只鸡兔同在一个笼子里，从上面数有35个头，从下面数有94只脚，问笼中分别有多少只鸡和兔？本节课要通过这个趣题，搭建从小学算式通往初中方程的“桥”．

3.1为何搭建“桥”——衔接的必要性

小学生在苏科版六年级下册第三单元“解决问题的策略”中学习“鸡兔同笼”，是以数和算式为主．由于一只鸡的脚数和一只兔的脚数不同，学生根据学习乘法时积累的基本活动经验，会自然想到假设全是鸡，也就是假设每只兔也有2只脚，这样就会得到70只脚，但是题目给的是94只脚，少了24只脚，因为假设每只兔有2只脚，少算了2只脚，少的24只脚，应该是12只兔少的脚，所以笼中有12只兔和23只鸡．当然也有同学联想到假设全是兔的方法，最后也得到有12只兔和23只鸡（如图1）．

初中生在苏科版七年级上册第4章“一元一次方程”中学习“鸡兔同笼”，是以等量关系和方程为主，由于鸡的头数＋兔的头数＝35头，鸡的脚数＋兔的脚数＝94足，设鸡有x只，则兔有（35－x）只，则鸡的脚数是2x，兔的脚数是4（35－x），由等量关系得到2x＋4（35－x）＝94，解方程得到x＝23，从而得到有12只兔和23只鸡．

由于小学数学中字母表示数的内容非常少，需要使用方程的场景也少，并且小学教材中并没有过多强调方程的背景，几乎都只是介绍了简易方程这种方法，比如：4＋x＝9，可能小学有这样类似的背景：小明有4元钱，妈妈再给他多少元，小明就有9元？解决这样的问题，本质上需要的是减法运算，没必要用到方程，所以，学习简易方程反而无法让学生意识到学习方程的必要性．

学生在初学方程时，总觉得用小学的算式挺好理解的，为什么要用方程呢？用算式的方法和列方程的方法究竟是两种不同的解题方法，还是从算式可以自然过渡到方程，两者之间是否存在一定的关联？这种关联应该怎么衔接？

小学的算式和初中的方程究竟有什么关联，笔者调查了很多初一上学期的学生，发现学生并不清楚，甚至有些学生给出了这样的解释：“小学只学过算式，当然只能用算式来做，初中学习了方程，当然采用方程来思考，如果在初中还用小学的方法，老师不会给分．”一些初中教师在教学过程中，也没有把小学算式和初中方程这两者之间进行自然衔接，没有搭建从小学的算式到初中的方程的“桥”，导致学生不知其所以然，只能被动去接受知识，因此搭建从小学算式到初中方程的“桥”是非常有必要的[3]．

3.2怎样构思“桥”——衔接的连续性

要想通过“鸡兔同笼”这节课，把小学的算式和初中的方程自然衔接起来，首先要了解小学生积累了哪些基本数学活动经验，通过调查发现90%以上的学生都自然联想到整数乘法的学习，都采用假设全是鸡或者假设全是兔的方法．而初中生学习方程后，解决“鸡兔同笼”问题，采用的是寻找等量关系，根据等量关系列出方程，然后解方程的方法．很显然，两者之间没有必然的联系，需要搭建一座“桥”把两者衔接起来，打通两者之间的关联，体现中小学数学知识学习的连续性．

衔接1代数式和方程的衔接

要想列出方程，前提是要找出等量关系，比如“鸡兔同笼”中的等量关系：鸡的头数＋兔的头数＝35只，鸡的脚数＋兔的脚数＝94只，鸡的头数×2＝鸡的脚数，兔的头数×2＝兔的脚数，遇到鸡的头数，兔的头数，鸡的脚数，兔的脚数都不知道时，我们想到用字母来表示数，用代数式来表示这些未知量．

衔接2数和代数式的衔接

小学生大多都采用假设全是鸡或者假设全是兔的方法，而初中的方程也是假設，只不过是设未知数，是假设有a只鸡，有（35－a）只兔．当然这里的a并不是35只鸡，也不是0只鸡，如何由假设全是鸡（即35只鸡）过渡到假设有a只鸡呢？

我们通过假设全是鸡，最后得到笼子里并不全都是鸡，这只是一个假设而已，那既然这样，可不可以假设有34只鸡和1只兔呢？通过这样的问题引发学生思考，学生通过计算并且同意这个假设后，再思考：可不可以假设有33只鸡和2只兔呢？引发学生再次证实．这样就慢慢搭建了从小学算式到初中代数式的“桥”，把数和代数式自然地衔接在一起（如表1）．

3.3何时搭建“桥”——衔接的合理性

“鸡兔同笼”这节课何时上比较合适呢？小学生在很长一段时间接触的都是具体的数，接触字母表示数的内容比较少．在初中学习了用字母表示数，学生逐渐理解由具体的数到抽象的式，能用代数式表示一些数量关系，接着又学习了整式的运算，这时开展“鸡兔同笼”这节课的学习，一方面，学生有了对数与式的理解，掌握了从具体到抽象的转化思想和整式运算的知识，这时候搭建从小学算式到初中方程的“桥”，是对学生从代数式到方程的衔接，具有明确的连续性，同时也为后面学习一元一次方程做好铺垫，打好基础．

“鸡兔同笼”这节课是根据小学和初中内容结构之间的关系，找到两者的衔接点，并且在合适的时候进行衔接——学生在初中学习了代数式的有关知识还没有开始学习方程，这个时候对学生开展“鸡兔同笼”的探究是建立在小学生学习数运算经验的基础上，慢慢发展提升的，根据学生学习力提升的规律来设计这样的课，这节课在时间上体现出衔接的合理性．

3.4怎样搭建“桥”——衔接的自然性

小学数学的学习主要以数与运算为主，初中数学的学习主要以代数式、方程、不等式和函数为主，两者的内容结构不同，解决“鸡兔同笼”的方法也有所不同．在小学用算式的方法，假设35只全是鸡，得到只有70只脚，根据脚数变少了，可以推算出兔的只数，还有其他学生假设35只全是兔，得到有140只脚，根据脚数变多了，也可以推算出鸡的只数，这是小学常用的算术方法，这节课笔者在此环节提出一个问题：我们一定要假设全是鸡，或者假设全是兔吗？解决这个问题，能假设不全是鸡，或者不全是兔吗？比如我们可不可以假设鸡有34只，兔有1只呢？试试看．

学生之前并没有想过这个问题，感到很好奇，有的学生开始尝试：假设有34只鸡，1只兔．34×2＝68，1×4＝4，68+4=72＜94，94－72＝22，少了22只脚，说明34只鸡中，把一部分兔当成了鸡，由于一只兔当成鸡少2只脚，22÷2＝11，所以34只鸡里有11只兔当成了鸡，再加上原来的1只兔，一共有12只兔，35－12＝23，所以鸡有23只．有的学生接着尝试：假设笼子里有33只鸡，2只兔，用类似的方法，也得到12只兔和23只鸡．

学生尝试后，进行了思考：我们假设全是鸡，假设全是兔，假设有34只鸡和1只兔和假设有33只鸡和2只兔，最后都能算出是23只鸡和12只兔（如表1）．也就是说，无论假设有多少只鸡（只要小于或等于35只），都可以得到鸡有23只，兔有12只.那我们就不需要一个一个去假设了，很自然地，学生想到用字母表示数，如果假设有a只鸡，那么就有（35－a）只兔．则a只鸡有2a只脚，（35－a）只兔有4（35－a）只脚，用含有a的代数式来表示．

对于初一的学生来说，这虽然不是一种新的方法，但是确是一个新的提法，或者是一个新的认识，是一个新的解决问题的思路，学生会产生好奇心.不管怎么假设，都可以仿照小学的方法把它算出来，由此可知，无论对鸡的只数怎么假设，结果永远是不会变的．很自然地，学生就能从小学的计算渐渐地想到鸡的只数其实是可以任意假设的，既然可以任意假设，那么可以怎么假设呢？这与初中刚学到的用字母表示数联系起来，学生自然地会想到一种方法，假设鸡有a只，兔有（35－a）只，a只鸡有2a只脚，（35－a）只兔有4（35－a）只脚，全部用含有a的代数式来表示．这样就形成了从算式到代数式非常自然的过渡．

（1）如果2a＋4（35－a）＜94，说明有一部分兔当成了鸡，由于一只兔当成一只鸡少2只脚，94－2a－4（35－a）＝2a－46，（2a－46）÷2＝a－23，所以有（a－23）只兔子当成了鸡，再加上原来的（35－a）只兔，a－23＋35－a＝12，所以一共有12只兔．

（2）如果2a＋4（35－a）＝94，说明正好有a只鸡，（35－a）只兔，直接算出a即可．

（3）如果2a＋4（35－a）＞94，说明有一部分鸡当成了兔，由于把一只鸡当成一只兔多2只脚，2a＋4（35－a）－94＝46－2a，（46－2a）÷2＝23－a，所以有（23－a）只鸡当成了兔，再加上原来的a只鸡，一共有鸡23－a＋a＝23只．

然后，学生观察（1）2a＋4（35－a）＜94；（2）2a＋4（35－a）＝94；（3）2a＋4（35－a）＞94．发现第（2）个最直接，最简明．因为正好是a只鸡，（35－a）只兔，第（2）个是等式，这是描述实际问题中的相等关系较为简明的一种形式，含有等号的式子是刻画现实世界数量关系的有效模型，这就是方程．这样就形成了从代数式到方程非常自然和合理的过渡．

3.5搭“桥”的目的——衔接的整体性

把义务教育阶段的核心素养进行有机衔接，这是教育者需要研究的一个问题.在《课标（2022年版）》中，数学课程和目标的描述强调整体性，课程目标的整体性决定了课程实施过程中，教师必须具备整体性视角，把数学学习看作具有内在一致性的整体结构.整体性视角是教师分析教材和设计学习过程的一个新的视角，可以帮助学生更好地理解学习，使得学生学得有趣、学得轻松、学得深刻．

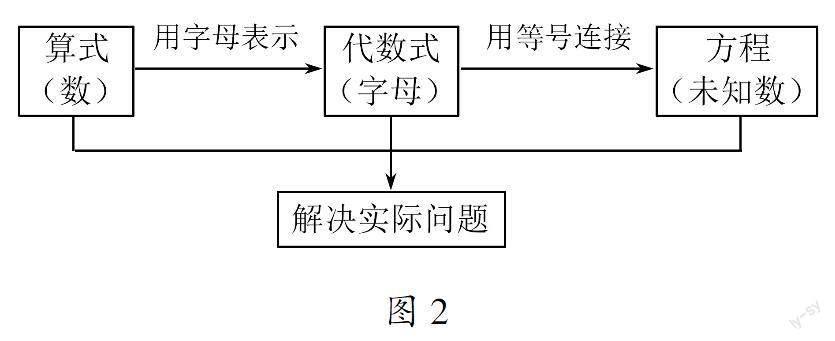
“鸡兔同笼”这节课，目的在于通过搭建小学算式到初中代数式，再到初中方程的“桥”，有了“桥”就产生了知识之间的关联，就形成了知识的整体架构（如图2）．教师教学没有一个整体观，学生对知识的学习浮于表面，不会进行融会贯通，主要原因之一就是教学的“碎片化”，忽视知识之间内在的关联．所以，教师教学要注重知识的内在联系，要具有整体观，要把每堂课教学的知识置于整体知识的体系中，注重知识的结构和体系，引发学生感受并体验数学知识的整体性．

3.6搭“桥”的好处——衔接的一致性

从教材的编排来说，大多采用螺旋上升的方式编排，渐进式深入，后续知识的学习都是在先前知识学习的基础上进行的，知识之间存在一致性．

从数学知识的角度来说，很多数学知识的学习具有一致性，比如：数与式的一致性，线段和角的一致性，三角形和四边形的一致性，方程和函数的一致性等等．

从学生学习的角度来说，很多数学知识的学习也具有一致性，比如：“鸡兔同笼”这节课，无论是从算式到代数式，还是从代数式到方程，让学生感觉到数学的学习并不散乱，而是具有规律性和一致性．

通过算式计算和通过代数式计算是一致的，小学生从假设全是鸡的计算和初中学生假设有a只鸡的代数推理计算可以说是完全一致的，不同之处在于一个是数的运算，一个是式的运算；一个是具体的，一个是抽象的；一个是特殊的，一个具有一般性．

从代数式到方程的过程中，出现从不等式到等式，其本质也具有一致性，代數式2a＋4（35－a）与94的关系：2a＋4（35－a）＞94，2a＋4（35－a）＝94，2a＋4（35－a）＜94．发现只有把不等式转化为等式，解决问题才最简单方便，当然解不等式和解方程的过程也具有一致性．

4教学反思

“鸡兔同笼”这节课，学生亲历从算式到代数式，再从代数式到方程的过程，学生积极主动去思考去探索，最后自然总结出：算式是由已知得到未知，是倒推，是逆向思维，一步只能得到一个结果，步骤比较多，比较复杂；代数式更具有一般性，它可以表示所有的假设，代数式计算和数的计算是一致的；而方程需要设未知数，找等量关系，理解题意比较容易，它把未知和已知都参与列方程中，列方程比较简单，方程是把很多步算式进行的一个整合；用方程比较方便、简明、清晰．这节课，无论是从算式到代数式，还是从代数式到方程，通过这样的必要性、连续性、合理性、自然性、整体性、一致性的教学设计，学生在教学中主动去体验和探索新问题，理解了知识间的来龙去脉，找到了知识之间的关联，提升了学生的代数推理能力，培养了学生良好的学习习惯，通过搭建的一座座“桥”把学生的旧知和新知有效衔接起来．

学生的学习是教育的最终目标，也是核心目标，教师在教学过程中，遇到知识内容、目标、表述上衔接不清晰、不明确，知识衔接不自然的时候，要深挖教材，找到知识发生发展的根源，为学生搭建通往新知的“桥”，为学生的学习助力，帮助学生更好地理解数学．

参考文献

[1]中华人民共和国教育部．义务教育数学课程标准（2022年版）[M]．北京：北京师范大学出版社，2022：5-6．

[2]曹一鸣．新版课程标准解析与教学指导（2022年版）[M]．北京师范大学出版社，2022.8：12-14．

[3]万涛．理清困惑，使教学更自然——对“因式分解”一课的教学体验[J]．中学数学杂志，2021（12）：24-28．

作者简介万涛（1984—），男，安徽临泉人，中学高级教师;南京市鼓楼区初中数学学科教学带头人，多次获得南京市教育案例一等奖和鼓楼区青年教师基本功大赛一等奖;主要从事初中数学体验教学和模式研究.

倪军（1967—），男，江苏宝应人，江苏省数学特级教师，江苏省优秀教育工作者，江苏省教学新时空名师课堂特聘专家，江苏省乡村教师培育站初中数学专家指导组成员;主要从事数学教育和研究工作;主持多项省重点规划课题，发表多篇论文．