New solitary waves and exact solutions for the fifth-order nonlinear wave equation using two integration techniques
Ahme H.Arnous ,Mohmm Mirzzeh ,Lnre Akinyemi ,Arzu Akulut
a Department of Physics and Engineering Mathematics, Higher Institute of Engineering, El Shorouk Academy, Cairo, Egypt
b Department of Engineering Sciences, Faculty of Technology and Engineering, East of Guilan, University of Guilan, Rudsar-Vajargah, Iran
c Department of Mathematics, Lafayette College, Easton, Pennsylvania, USA
d Department of Mathematics Computer, Faculty of Art Science, Eski ¸s ehir Osmangazi University, E ¸s kisehir, Turkey
Keywords: Enhanced Kudryashov method Riccati equation Water waves Fifth-order nonlinear model Solitons
ABSTRACT In this paper,we discussed the enhanced Kudryashov’s and general projective Riccati equations techniques for obtaining exact solutions to the fifth-order nonlinear water wave (FONLWWE) equation.Using the enhanced Kudryashov’s method,we were able to achieve solitary wave and singular soliton solutions.Solitary-shock hybrid wave,singular soliton,and periodic wave solutions were discovered when we employed the general projective Riccati equations approach.We can say the given methods are effective and powerful for obtaining exact solutions.Our findings in this paper are critical for explaining a wide range of scientific and oceanographic applications involving ocean gravity waves and other related phenomena.
1.Introduction
Nonlinear evolution equation (NLEE) and wave equations are partial differential equations including first or second-order derivatives with respect to the time variable.Nonlinear partial diffrential equations (NLPDEs) have a very important place in plasma physics,optics,hydrodynamics,quantum electronics,fluid mechanics and so on.Since the solution of NLPDEs is complex and difficult,there has been a rise in interest in these equations in recent years.Many mathematicians have introduced methods for solving these equations like the inverse scattering approach [1],the tanh method [2],the symmetry reduction [3],the modified Kudryashov method [4],the exponential method [5],the generalized Kudryashov method [6],the new auxiliary equation method[7],the generalized exponential rational function method [8],Hirota bilinear method [9],extended simple equation method [10],sub-equation method [11],the improved-expansion method[12],the Riccati-Bernoulli Sub-ODE method [13],the improved generalized Riccati equation mapping method [14],and so on[15–35].
The fifth-order nonlinear water wave equation (FONLWWE),which was constructed by Olver as an evolving version of the classical Boussinesq model [36],has been the focus of this study.The FONLWWE foru=u(x,t) is considered as [37] :
whereci,i=1,...,5 are constants with the coefficientsc1andc2are independent of the depth in which the horizontal velocityu(·) is measured.This equation comes from the water wave problem for long,small amplitude waves over the shallow horizontal bottom.Lots of researchers studied with the FONLWWE such as Hosseini et al.derived W-shaped and other solitons by Kudryashov methods [37].Lu and Wang obtained the analytical soliton solutions by using special truncated expansions [38].Hosseini et.al.applied the invariant subspace scheme for obtaining exact solutions of the given model [39].Solitary wave solutions are obtained for the model using the modified extended tanh-method reported by Ali and Soliman in [40].Kaya used the Adomian decomposition method for finding the solitary waves in [41].The main idea of the present study is to revisit and improve the previous studies already conducted on the suggested model.To achieve this,we applied two different methods to get novel exact solutions of Eq.(1) with the help of enhanced Kudryashov’s and general projective Riccati equations methods.The modified Kudryashov technique [4,42] and the generalized Kudryashov method [6] are two versions of Kudryashov methods that have been described in the literature.When we compared these approaches to the present enhanced Kudryashov method,we can see that the auxiliary equations employed are different,and the balance number obtained is also different.The outcomes in this study are new,and they may be useful in understanding the dynamics of physical behaviors.The application of these mathematical tools to the suggested model has never been presented in the literature,and they may be useful in understanding the dynamics of physical behaviors.
The rest of this paper is structured as follows: In Section 2,the enhanced Kudryashov’s method will be described and then applied to the given model.In Section 3,the second method namely the general projective Riccati equations method will be described and also applied to the given model.The graphical illustration and discussion will be detailed in Section 4.In the last section,conclusions will be given.
2.The enhanced Kudryashov’s method (EKM)
Consider the NLEE as follows:
wherexandtare independent variables anduis dependent variable.The following are the EKM’s main steps [43,44]:
Firstly,we will use the following wave transformation for reduced Eq.(2) to a nonlinear ordinary differential equation (NODE):
wherekandvare constants to be determined later,U(ζ) denotes the amplitude component of the soliton solution andvis the speed of the soliton.When we apply the specified wave transformation to Eq.(2),we get the reduced NODE as:
According to the procedure,the exact solutions of the Eq.(4) may be examined as
whereλ0,λij(i,j=0,1,...,M) are constants that are calculated later.The functionsR(ζ) andQ(ζ) take the form below:
The solutions of Eqs.(6) and (7) are expressed as
wherea,η,b, andχare arbitrary constants.
The homogeneous balance approach allows us to calculate the balance numberM.So,in Eq.(4),we can calculateMby equating the highest power of the nonlinear term(s) with the highest power of the highest order derivative.Thereafter,we derive a polynomial ofR′(ζ),R(ζ), andQ(ζ) by substituting Eq.(5) into Eq.(4) together with Eqs.(6) and (7).In this polynomial,we collect all terms with the same powers and equate them to zero to generate a system of algebraic equations that can be solved using Maple or Mathematica to extract the unknown parametersk,v,a,b,η,χ,λ0,λij,(i,j=0,1,...,M).Lastly,the exact solutions of (2) are obtained.
2.1.Application of EKM
We will apply EKM to the suggested model in this subsection.Applying the given method to the given model,we will reduce the equation with the help of wave transformation.For this situation,If we substitute (3) into (1),we get following NODE:
Also,Eq.(10) can be rewritten as
Here,A1can be used to determine the value of the soliton speedvas follows:
According the balance method,If we balanceU(4)withUU′′,we getM=2.Thus,exact solution is written in the following form
Substituting Eq.(14) into Eq.(11),together with Eqs.(6) and (7).Then,we acquire some polynomials withQ(ζ),R(ζ) andR′(ζ).Later,we gathered all the terms of the same powers and set them to zero.Finally,we solve an obtained system of algebraic equations by the Mathematica or Maple and results in the following.
Consequently,the exact solution of Eq.(1) is given as follows:
Settingχ=±4a2in solution Eq.(16).Consequently,we have

Fig.1. The 3D and 2D wave profile of Eq.(17) with c1=c2=c3=c4=c5=0.1 and k=0.55.
Consequently,the exact solution of Eq.(1) is given as follows:
Settingχ=±4a2in solution Eq.(20).Consequently,we have
Consequently,the exact solution of Eq.(1) is given as follows
If we setη=±bin Eq.(24),we get
Consequently,we obtain the exact solution of Eq.(1) as follows
If we setη=±bin Eq.(28),we get
The recovered solitons of the obtained exact solutions are solitary wave and singular soliton solutions in all results.
3.The general projective Riccati equations method (GPREM)
In this section,we describe the GPREM [45,46].The main steps are given as follows:
According to the method,we can assume that Eq.(4) has exact solution as follows:
whereα0,βi, andαi,(i=0,1,...,M)are constants to be computed.The functionsφandψsatisfy the following NODEs:
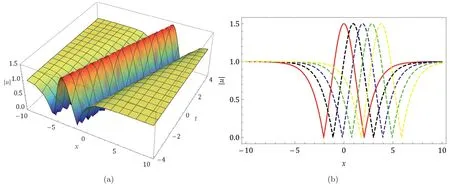
Fig.2. The 3D and 2D wave profile of Eq.(21) with c1=c2=c3=c4=c5=0.1 and k=0.50.

Fig.3. The 3D and 2D wave profile of Eq.(40) with δ=0.6,c1=c2=c3=c4=c5=0.1 and k=0.4.
where
whereσ >0 andδare arbitrary constants.The solutions of Eq.(32) are listed as follows:
The balancing approach allows us to calculate the positive integer numberM.In the preceding part,we have discussed this balancing approach.We generate a polynomials ofφandψby substituting Eq.(31) into Eq.(4) together with Eqs.(32) and (33).We gather all terms with same powers in these polynomials and equate them to zero to create a system of algebraic equations that can be solved using Maple or Mathematica to acquire the unknown parametersk,v,σ,δ,α0,αi,andβi,(i,=0,1,...,M).Lastly,the exact solutions of Eq.(2) are obtained.
3.1.Application of PREM
We obtainedM=2 in the previous section and so we get
Substituting Eq.(38) into Eq.(11) without ignoring Eqs.(32) and(33).Then we haveφandψpolynomials.We can solve these polynomials by gathering all terms with the same powers and equating them to zero,generating a system of algebraic equations that can be solved using Maple or Mathematica to yield the following outcomes.
Then,the corresponding solutions of Eq.(1) are
Then,the corresponding solutions of Eq.(1) are
Then,the corresponding of solutions Eq.(1) are
Then the corresponding solutions of Eq.(1) are
The obtained solutions are solitary-shock hybrid wave solution for the first result,while the other solutions considered as singular soliton and periodic wave solutions.
4.Graphical illustration and discussion
The most effective way to grasp the actual physical behavior of real-world situations is through graphic representation.In this section,we have provided the absolute graphical behavior of certain solutions of the considered model.In particular,the graphs of solutions in Eqs.(17),(21),(40),and (44).Using appropriate values of parameters,Figs.1,2,3 depicted the bright solitons while Fig.4 represents the periodic solution.The 2D plots are depicted with differenttin all graphs wheret=0 (solid red),t=1(dashed blue),t=2 (dashed black),t=3 (dashed green),andt=4(dashed yellow) respectively.The enhanced Kudryashov’s and general projective Riccati equations techniques were significantly used in this study to portray various dynamical wave patterns of computed analytical wave solutions to the considered equation.As a result,a huge number of wave solutions have been generated that may be utilized to explain the underlying wave profiles of complicated physical phenomena in disciplines including ocean and optical physics,hydrodynamics,nonlinear dynamics,plasma physics,marine engineering,and many more.
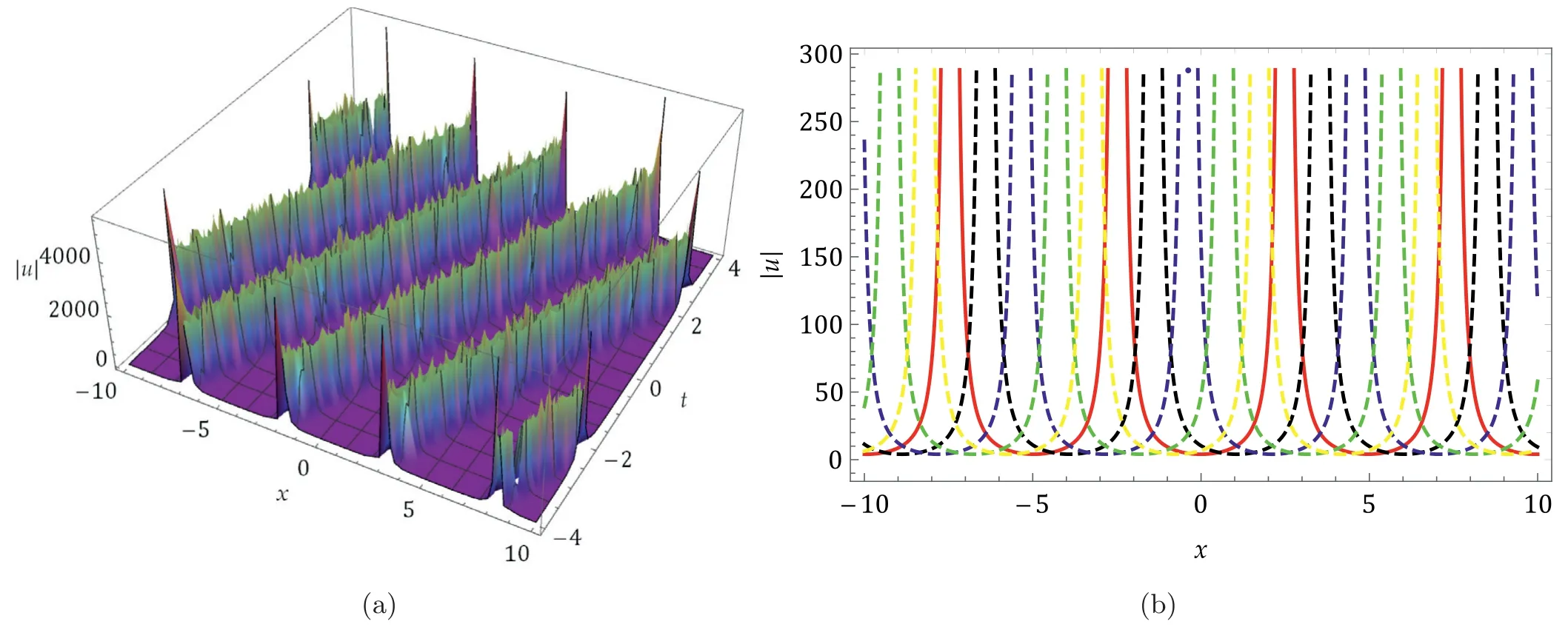
Fig.4. The 3D and 2D wave profile of Eq.(44) with δ=0.001,c1=c2=c3=c4=c5=0.1 and k=0.4.
5.Conclusions
In this work,two different techniques,the enhanced Kudryashov’s and the general projective Riccati equations methods have been applied to FONLWWE for obtaining the exact solutions.We obtained solitary wave and singular soliton solutions with the help of the enhanced Kudryashov’s method.When we used the general projective Riccati equations method,solitary-shock hybrid wave solution,singular soliton and periodic wave solutions were obtained.Also,based on our knowledge,we can use the obtained exact solutions in some physical and ocean engineering phenomena.Different methods can be applied to the given model in future research works.The methods presented are helpful,powerful,and successful for generating exact solutions to NLPDEs,and they may be applied to a variety of NLPDEs,including fractional order NLPDEs.Finally,we concluded that the obtained results in this study are new,and that,to the best of our knowledge,the application of these mathematical tools to the proposed model has not been previously reported in the literature,and that they may be useful in understanding the dynamics of physical behaviors.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
 Journal of Ocean Engineering and Science2023年5期
Journal of Ocean Engineering and Science2023年5期
- Journal of Ocean Engineering and Science的其它文章
- Numerical treatment of temporal-fractional porous medium model occurring in fractured media
- Optimal Kalman-like filter for a class of nonlinear stochastic systems
- Dynamic quantitative risk assessment of LNG bunkering SIMOPs based on Bayesian network
- New soliton wave solutions of a (2+1)-dimensional Sawada-Kotera equation
- Review of enhancement for ocean thermal energy conversion system
- Prediction of residual tensile strength of glass fiber reinforced polymer bars in harsh alkaline concrete environment using fuzzy metaheuristic models
