均值方差保费原理下带有时滞的鲁棒最优再保险和投资策略
胡景铭, 刘 伟, 阎 方, 胡亦钧
(1.新疆大学数学与系统科学学院,乌鲁木齐 830046; 2.武汉大学数学与统计学院,武汉 430072)
0 引言
保险公司的最优再保险和投资策略一直是保险精算学术界及业界十分关注的问题。作为保险中的保险,再保险可以使保险公司突破资金和规模的限制,尽可能的拓展业务。保险人通过购买再保险将部分索赔风险转移给再保险公司,控制损失,实现公司的稳定经营。此外,保险人通过将公司的资产投资于金融市场,以提高收益,实现资金的增值保值,降低通货膨胀所带来的风险。近几十年来,很多学者运用随机控制理论对保险公司的最优再保险和投资问题进行了广泛研究。例如,Browne[1]、David Promislow 和Young[2]、Hipp 和Taksar[3]、Liang 等[4]、Zhao 等[5]、Zhang 等[6],其中Liang 等[4]研究了风险资产价格模型中收益率服从均值回复O-U 过程下的最优再保险和投资问题,以终端时刻期望效用最大化为优化准则,得到了最优策略和相应值函数的显式表达式。Zhang 等[6]采用广义均值方差保费原理,以终端时刻期望效用最大化和最小破产概率为优化准则对最优再保险和投资策略进行了研究。
保险公司的历史业绩往往会对当前的财富产生影响。如果一个保险公司的历史业绩优秀,获得了更多的收益,该保险公司可能将部分收益通过股息等形式派发给股东。反之,如果一个保险公司的历史业绩不佳,为了实现最终的业绩目标,往往需要进一步的内外部融资。鉴于这种时滞现象的客观存在,在研究保险公司最优再保险和投资问题时,有必要将时滞效应融入进最优再保险和投资策略中。Shen 和Zeng[7]首次将时滞效应引入保险公司的最优再保险和投资问题,通过与过去财富相关的瞬时资金流入或流出函数对时滞效应的影响建模,给出了最优再保险和投资策略的显式表达式。A 和Li[8]在时滞效应下最优再保险和投资问题的研究中进一步考虑了风险资产模型为Heston 模型,再保险形式为超额损失再保险。Deng 等[9]在可违约的市场下,研究了带有时滞效应的保险公司最优再保险和投资问题。Zhang 和Chen[10]、Li 和He[11]和Bai 等[12]分别对服从跳跃扩散模型的风险资产,保险公司博弈和CEV 模型的最优再保险和投资问题,在时滞效应下进行了研究。
另一方面,上述的大多数研究均基于一个假设:即假设概率空间上的概率测度是已知的。然而,概率空间上单一的概率测度往往不能精确地反应市场的真实情形,概率测度的偏差会对最优策略产生影响。这种概率测度不精确所导致的不确定性就是所谓的模型不确定性。关于模型不确定性下最优控制问题的研究,Maenhout[13]研究了最优投资和消费问题,给出了在模型不确定性下随机控制问题的求解方法。Yi 等[14]研究了模型不确定下的最优再保险和投资问题。Guan 和Liang[15]假设风险资产由无风险资产、债券、通胀保值债券和股票组成,研究了保险公司最优再保险和投资策略。Deng 等[16]研究了广义均值方差保费原则下保险公司的鲁棒最优再保险和投资问题。
本文提出一种新的最优再保险和投资模型,在该优化模型中同时考虑了模型的不确定性和保险公司的时滞效应。此外,风险资产的收益率是随机收益率模型。在终端时刻期望效用最大为优化准则下,本文利用随机控制理论,通过求解相应的HJB 方程,得到了最优再保险和投资策略和相应值函数的显式表达式。同时,本文给出了验证定理。最后,通过数值分析,讨论了模型主要参数对最优策略的影响,数值分析也验证了本文所提模型和所获结果是有效的。
本文其余安排如下:第1 部分叙述模型和假设条件;第2 部分为本文的主要结论;第3 部分讨论模型中主要参数对最优策略的影响;第4 部分是本文的总结。
1 模型和假定
假设(Ω,F,P)是一个完备的概率空间,{W(1)(t),W(2)(t),W(3)(t)}是定义在其上的三个标准布朗运动,F={Ft}t∈[0,T]是由{W(1)(t),W(2)(t),W(3)(t)}产生的σ-代数流,T >0 为终端时刻。假定金融市场中的交易可持续进行,所有资产可以无限分割,且保险人在t时刻做出的任何决策都基于Ft。
假设保险公司盈余过程为M(t),满足
其中m >0 为保费率,h0>0 为索赔率,σ0>0 为索赔过程的波动率。假设保险公司通过购买比例再保险来转移部分索赔风险,记q(t)∈[0,1]为自留比例。根据广义均值–方差保费原理[6],支付给再保险公司的保费为
其中Λ >0,Λ0>0 为再保险公司的安全载荷系数。令η= (m −h0)/σ20为保险公司的安全载荷系数,满足基本条件0≤η ≤Λ。由q(t)∈[0,1]及q(t)满足的净利润条件
得到
记
此时,保险公司盈余过程可表示为
保险公司可以将盈余投资于由一个无风险资产和一个风险资产组成的金融市场。设无风险资产的价格S0(t)表示为
其中r >0 为无风险利率。风险资产的价格S(t)服从
其中k1>0 为风险资产的波动率。风险资产预期收益率a(t)为均值回复O-U 过程,
其中k >0,βa >0, ¯a >0 为常数。设W(1)(t)和W(2)(t)之间相互独立,W(2)(t)和W(3)(t)之间的相关系数为ρ。
记X(t)为保险公司在t时刻的财富,Y(t)和Z(t)分别代表过去时间[t −h,t]的历史综合业绩和历史逐点业绩,即
其中δ ≥0,h >0 为常数。假设g(t,X(t)−Y(t),X(t)−Z(t))为资金流入或流出,其中X(t)−Z(t)表示过去时间[t −h,t]上的绝对收益或损失,X(t)−Y(t)表示过去时间[t −h,t]上的平均收益或损失的均值。这种与历史财富相关的瞬时资金流入或流出可能出现在以下情况。当X(t)>Z(t),X(t)>Y(t)时,保险公司历史业绩良好,可能将部分收益作为股息发给股东。这是资金流出的情况,即g >0。相反,当X(t)<Z(t),X(t)<Y(t)时,保险公司历史业绩不佳,可能需要通过注资,来弥补过去的损失,以实现最终的业绩目标。这相当于资金的流入,即g <0。设保险公司初始财富为x0,A(t)为投资于风险资产的金额,令Xπ(t)为再保险–投资策略π(t) :={(A(t),q(t)) :t ∈[0,T]}下的财富过程,则带有时滞的保险公司财富过程Xπ(t)可以描述为
对于任意的t ∈[−h,0],Xπ(t) =x0>0,即保险公司在[−h,0]期间未进行投资和保险业务。历史综合业绩的初始值为Y π(0)=x0(1−eδh)/δ。
假设瞬时财富流入或流出函数为线性的,即
其中B >0,C >0 为常数。
有关最优再保险和投资问题的研究,大多数基于一个假设:即假设概率空间上的概率测度是已知的。然而,该概率空间上单一的概率测度往往不能精确地反应市场中的真实情形。本文考虑模型的不确定性,将传统问题中的概率测度称为参考测度,并通过测度变换的方法引入一系列与参考测度等价的测度,进而求解稳健的最优策略。定义等价测度Q的集合
定义1 对于任意的t ∈[0,T],策略π(t) :={(A(t),q(t)) :t ∈[0,T]}称为可接受的,如果它是Ft-循序可测的,且满足:
(i)q(t)∈[¯q,1];

其中U(·)表示效用函数,Et,x,y,a[·]是给定Xπ(t) =x,Y π(t) =y,a(t) =a的条件期望,Q∗是最稳健的等价测度。
记Π为所有可接受策略的集合。

则V(t)是概率测度P下的鞅。由Girsanov 定理,概率测度Q下的布朗运动为
此时,模糊厌恶型保险公司的盈余过程为

其中ϕi为模型厌恶系数,描述决策者对模型准确性的不确定程度。关于相对熵和鲁棒控制问题可参考文献[13–15]。
2 最优控制问题求解

一般带有时滞的最优控制问题是无限维的,为了使问题是有限维且可解的,假设
本文以终端时刻的期望效用最大化为优化准则,同时,采用的效用函数为指数效用。由于定义的值函数与效用函数有关,因此值函数的具体形式应与效用函数有关,即值函数的具体形式应为指数函数。此外,本文参考文献[4]的研究及方程中a(t)与x、y的关系,风险资产预期收益率a(t)在值函数中为如下形式。为证明所求解的方程就是值函数,本文将通过验证定理(即定理2)提供理论支持。求解值函数的形式为

根据一阶条件,可得

根据(13)式和(14)式,解得
根据(12)式,有β=Ceδh,B −βδ= (r −B −C+β)β。将A∗(t)、q∗1(t)和(13)式代入HJB 方程(14),整理可得
由x+βy/= 0,有x+βy前系数为0,即lt+l(r −B −C+β) = 0。根据终端条件l(T)=1,解得
进一步,考虑方程如下形式的解
其中边界条件为G(a,T)=0。对G(a,t)求各阶偏导数,有
令
有
将Gt、Ga和Gaa代入(18)式,整理得
由a2/=0,且K(T)=0,解得
其中
由a/=0,且J(T)=0,解得
其中
由L(T)=0,解得
令
由于λ、n、ϕ1均非负,q∗1(t)随时间t单调递增。根据净利润条件,保险公司自留水平q∗(t)∈[¯q,1],其中
因此,再保险策略q∗(t)可以分为三种情况:

其中l(t)、f、K(t)、J(t)和L1(t)分别由(16)式、(17)式、(19)~(21)式给出。
由L(¯t)边界条件确定。
定理1 对于鲁棒控制问题(10),满足财富过程(8)式和(9)式的最优投资策略为
其中t ∈[0,T]。

相应的值函数为(23)式。

则定理1 中给定的H(t,x,y,a)是值函数,π∗(t) ={A∗(t),q∗(t)}是鲁棒最优策略,最稳健的等价测度如下
定理2 的证明,可参考文献[17–19]。
3 敏感性分析
3.1 再保险策略分析
图1 分析了时滞参数δ对再保险策略q∗(t)的影响。随时滞参数δ增加,再保险策略q∗(t)减少。当δ增加,保险公司会购买更多的再保险,减小自留的保险业务。由于历史综合业绩Y(t)和资本流入或流出函数g(t,Xπ(t)−Y π(t),Xπ(t)−Zπ(t))的定义,当参数δ增加,资本流出增加。因此,保险公司减少自留比例。图2 分析了时滞参数h对再保险策略q∗(t)的影响,再保险策略q∗(t)随时滞参数h增加而减少。当h增加,保险公司将减少自留份额。保险公司考虑更长时间的历史业绩,会增加历史业绩对终端财富的影响程度。因此,保险公司将更加谨慎,购买更多的再保险以减少自留风险。图3 分析了时滞参数β对再保险策略q∗(t)的影响。时滞参数β越大,再保险策略q∗(t)越小。当β增加,保险公司将采用更为保守的再保险策略,购买更多的再保险。当β增加,历史综合业绩Y(t)会对终端财富效用产生更大影响。所以保险公司为降低风险,减少自留比例。

图1 时滞参数δ 对再保险策略q∗(t)的影响

图2 时滞参数h 对再保险策略q∗(t)的影响

图3 时滞参数β 对再保险策略q∗(t)的影响
图4 分析了参数ϕ1对再保险策略q∗(t)的影响。随参数ϕ1增加,再保险策略q∗(t)减少。当ϕ1增加,保险公司将减少自留风险。由于模糊厌恶程度增加,保险公司将不愿意承担较大的索赔风险。图5 分析了市场参数r对再保险策略q∗(t)的影响,再保险策略q∗(t)随市场参数r的增加而减小。利率越大保险公司自留比例越小,利率增加保险公司将更愿意把风险转移给再保险公司,从而获得更多收益。图6 分析了时滞效应和鲁棒因素对再保险策略q∗(t)的影响。考虑时滞效应和鲁棒因素后再保险策略q∗(t)减少,保险人会采取更为稳健的再保险策略,只愿意保留较小风险。这也充分说明时滞效应可以增加保险公司财富的稳定性,鲁棒可以降低模型不确定性带来的风险。

图4 参数ϕ1 对再保险策略q∗(t)的影响

图5 市场参数r 对再保险策略q∗(t)的影响
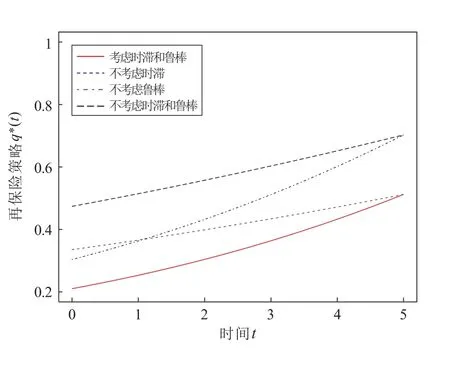
图6 时滞和鲁棒对再保险策略q∗(t)的影响
3.2 投资策略分析
图7 分析了时滞参数δ对投资策略A∗(t)的影响,投资策略A∗(t)随δ增加而减少。当δ增加,保险公司将减少风险资产的投资。由于δ增加,保险公司资本的流入或流出增加。保险公司为使财富更为稳定,从而减少风险资产的投资。图8 分析了时滞参数h对投资策略A∗(t)的影响。时滞参数h越大,投资策略A∗(t)越小。考虑历史财富时间的增加,风险资产投资将减少。考虑更长时间的历史业绩,会增加资本流入或流出对终端财富的影响。因此,保险公司将持有更少的风险资产。图9 分析了时滞参数β对投资策略A∗(t)的影响。随β增加,投资策略A∗(t)减少。时滞参数β越大,风险资产投资越少。β增加会增加历史业绩对终端财富的影响,然而保险公司希望减少风险资产波动带来的风险。因此,减少风险资产投资。

图7 时滞参数δ 对投资策略A∗(t)的影响
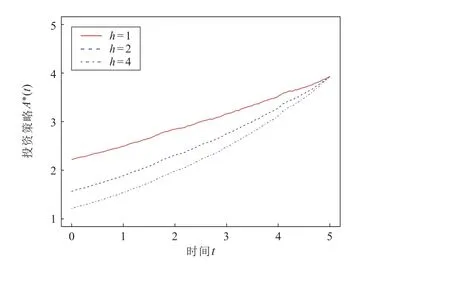
图8 时滞参数h 对投资策略A∗(t)的影响

图9 时滞参数β 对投资策略A∗(t)的影响
图10 和图11 分析了参数ϕ2和ϕ3对投资策略A∗(t)的影响。参数ϕ2和ϕ3越大,投资策略A∗(t)越少。当ϕ2和ϕ3增加,保险公司将减少风险资产的投资。保险人对风险资产模型的不确定程度更大,从而不愿意承担较大的金融市场风险,并且参数ϕ2对投资策略有较大的影响,而参数ϕ3对投资策略的影响较小。图12 分析了时滞效应和鲁棒因素对投资策略A∗(t)的影响,时滞效应和鲁棒因素导致投资策略A∗(t)减少。考虑时滞效应和鲁棒因素后,保险公司将减少金融市场带来的风险,使模糊厌恶性保险公司的财富更具稳健性、确定性。

图10 参数ϕ2 对投资策略A∗(t)的影响

图11 鲁棒参数ϕ3 对投资策略A∗(t)的影响

图12 时滞和鲁棒对投资策略A∗(t)的影响
图13 分析了利率r对投资策略A∗(t)的影响,投资策略A∗(t)随利率r增加而减少。当利率r增加,保险公司将减少风险资产的投资。很直观,利率增加无风险资产可以获得更多的收益,从而减少风险资产的投资。图14 分析了风险资产模型中的波动率k1对投资策略A∗(t)的影响。波动率k1越大,投资策略A∗(t)越少。当k1增加,保险公司将采用更保守的投资策略。波动率越大表示金融市场风险越大,从而减少的风险资产投资。

图13 市场参数r 对投资策略A∗(t)的影响
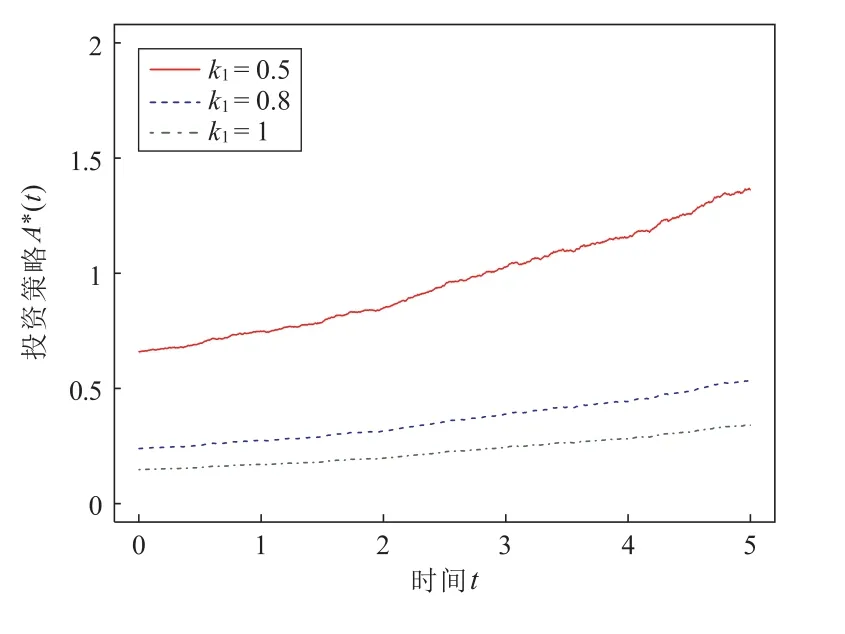
图14 市场参数k1 对投资策略A∗(t)的影响
4 结论
本文考虑了带有时滞效应的保险公司鲁棒最优再保险和投资问题。保险公司购买比例再保险来转移部分索赔风险,并且投资于由一种无风险资产和一种风险资产组成的金融市场。其中,风险资产预期收益率服从均值回复O-U 过程,描述金融市场的预期收益发生偏差带来的风险。运用动态规划原理,以终端财富的指数效用期望最大为优化准则,得到了最优再保险–投资策略和相对应值函数的显式表达式,并且给出验证定理。最后,通过数值分析说明模型中主要参数对最优策略的影响。
本文发现再保险策略不仅依赖于保险市场的参数,还依赖于无风险资产的参数,然而风险资产的参数和风险资产预期收益率的参数对再保险策略没有影响;投资策略依赖于无风险资产的参数,风险资产的参数和风险资产预期收益率的参数,然而保险市场的参数对投资策略没有影响。考虑时滞效应和鲁棒因素会对最优再保险–投资策略产生较大的影响,考虑时滞效应可以增加保险公司财富的稳定,考虑模型不确定性能有效降低概率测度不精确带来的风险。这些结论为保险公司风险控制和资产分配提供理论依据。

