题不在多有悟则灵
——谈一道高考题的探究

2010-02-02 02:31傅阿勇虞金龙绍兴市第一中学浙江绍兴312000

●傅阿勇虞金龙 (绍兴市第一中学浙江绍兴 312000)

●傅阿勇虞金龙 (绍兴市第一中学浙江绍兴 312000)

近几年高考试题稳中有变，变中求新，每年都有几道考题与“旧题”似曾相识．教师在讲课时应该遵循“少而精”的原则，对重点、热点问题应进行专门、集中的讲解和探究，要“挖得深，讲得透”．本文谈谈一道高考题的探究，旨在抛砖引玉．

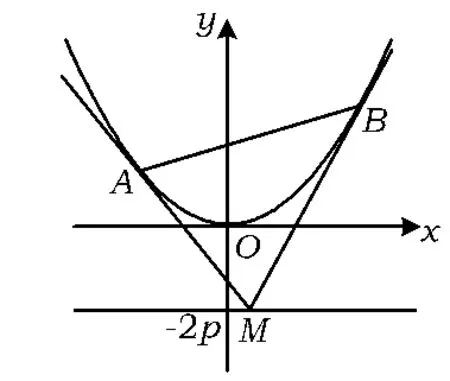
图1

题目如图1，设抛物线方程为 x2=2py(p＞0)，M 为直线y=－2p上任意一点，过点M引抛物线的切线，切点分别为 A，B，求证:点 A，M，B 的横坐标成等差数列．

因此点A，M，B的横坐标成等差数列．

教师往往讲到此为止，但笔者以为这样为讲题而讲题，上课的效果会大打折扣．若能仔细悟题，则可以大大提高课堂教学的有效性．

1 悟其解题方法，寻找一题多解

进行一题多解可以启发和引导学生从不同角度、不同思路、运用不同的方法来解答问题，有利于充分调动学生思维的积极性，提高学生综合运用已学知识解答数学问题的能力;有利于锻炼学生思维的灵活性，促进学生知识与智慧的增长;有利于开拓学生的思路，引导学生灵活地掌握知识之间的联系，培养和发挥学生的创造性．

教师在教学时要认真研究解题过程，对解题过程出现的一些特征、结果进行推广，变特殊为一般，让学生在更高的角度上、更高的层次上重新认识问题，这样做有助于促使学生对问题产生新的认识，有助于培养学生的探索精神与创新意识，对提高数学课堂教学的有效性有着十分重要的作用．

结论1设抛物线方程为x2=2py(p＞0)．若M(x0，y0)是抛物线外任意一点，过点M引抛物线的切线，切点分别为A，B，则点A，B，M的横坐标成等差数列．

结论3P(x0，y0)是抛物线x2=2py上任意一点，过点P作抛物线的切线，切点分别为A，B，则直线AB的方程为x0x=p(y+y0)．

证明设 A(x1，y1)，B(x2，y2)，由结论 2 可知，过点A，B的切线方程分别为

因为点 A(x1，y1)，B(x2，y2)都在直线 x0x=p(y+y0)上，而过点A，B有且只有1条直线，所以直线AB的方程为x0x=p(y+y0)，结论3成立．

同理可得以下一般性结论．

结论4设抛物线方程为y2=2px(p＞0)．若M(x0，y0)是抛物线外任意一点，过点M引抛物线的切线，切点分别为A，B，则点A，B，M的纵坐标成等差数列．

结论5P(x0，y0)是抛物线y2=2px上任意一点，过点P作抛物线的切线，则切线的方程为y0y=p(x+x0)．

结论6P(x0，y0)是抛物线y2=2px上任意一点，过点P作抛物线的切线，切点分别为A，B，则直线AB的方程为y0y=p(x+x0)．

在教学中，要对命题进行不同方向、不同情形、不同背景的变式，充分揭露问题的本质，揭示不同知识点的内在联系，把不熟悉的知识变为熟悉的知识，做到举一反三，可以有效减轻学生负担，大大提高课堂教学的有效性．

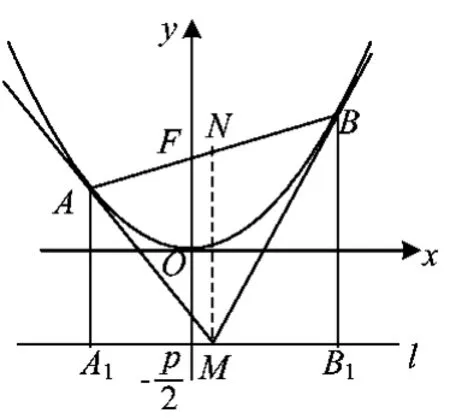
图2

如图2，取AB中点为N，连结MN．设过点M与y轴垂直的直线为 l，过点 A作AA1⊥l，过点 B 作 BB1⊥l．由例题结论可知MN是梯形ABB1A1的中位线，当 AB过抛物线焦点F，点M在准线y=－上时，

|AB|=|AF|+|BF|=|AA1|+|BB1|=2|MN|，此时以线段AB为直径的圆过点M，即MA⊥MB，由此可以得到一个很好的变式:

(1)点M必在准线上;

(2)FM⊥AB;

(3)MA⊥MB;

(4)|FM|2=|FA|·|FB|．

证明略．

抛物线是圆锥曲线的一种，运用类比思想可以在椭圆、双曲线中得到如下结论:

(2)略．

这样可以把不熟悉的切线问题变为熟悉的焦点弦问题，由此又可以得到下面的变式．

类似结论还有很多，这里不再一一举例．

在高三数学复习中，对例题要进行多方面的感悟，悟其解题方法、悟其解题过程、悟其解题特征、悟其类比思想，举一反三，触类旁通．不仅要做一题懂一题，而且要做一题懂一片，这样才能使复习起到最大的作用．