存贷款利率隐含期权定价的蒙特卡罗模拟及其改进
刘凤琴,马俊海,戈晓菲
(1.浙江财经学院信息学院,浙江 杭州 310018;2.浙江财经学院金融学院,浙江 杭州 310018)
一、引 言
随着我国金融市场的不断开放和利率市场化进程的推进,市场利率的波动越来越频繁和激烈,给我国商业银行带来了新的机遇和挑战:利率的频繁波动将使商业银行面临更大的期权性风险。因此研究银行等金融机构资产、负债隐含期权的定价技术对我国商业银行在产品开发和风险管理等方面都具有重要的理论及现实意义。在隐含期权的定价方面,国内外学者取得了许多重要研究成果。从国际上所取得的研究成果来分析,Brent W.,Richard(1998)利用蒙特卡罗方法对亚式期权中的隐含期权进行了定价分析,并通过参数估计得出了含有亚式期权的债券的价格[1];Brooks R(1996)还通过横截面数据对利率水平和CDs中隐含期权价值作了敏感性分析[2];Hatem Ben-Ameur(2006)的研究发现隐含期权的风险还可能来源于资产负债凸性的改变而导致资产、负债价格发生不可预期的改变,同时对存款当中的隐含期权进行了研究,分析了定期存款中存在有利于存款人选择或不选择提前支取的特权及行使特权的时间特征[3]。国内的隐含期权研究近几年发展也很快,郑振龙等(2004)则对存贷款产品中隐含期权的定价作了详细的研究,他们用无套利定价方法为存贷款产品中隐含期权进行了定价,并得出了我国银行存贷款利差过低的结论[4];夏和平等 (2007)就隐含期权条件下银行资产、负债利率风险控制进行了研究,指出了隐含期权条件下银行资产、负债的利率风险控制策略[5]。
由上分析可知,近些年来国内外关于银行隐含期权定价问题的研究取得了一定的研究成果,但是仍然主要集中在对含有隐含期权的利率风险的测量方面,而对于存贷款中隐含期权的定价则缺乏研究,特别是基于利率动态变化的存贷款的提前执行情况。另外在研究方法上,前人提出的无套利分析方法、微分方程法等都是基于一系列苛刻的假设,在更复杂的情况下 (如加入利率的跳跃因子)可能无法得出精确的解。而蒙特卡罗模拟方法基于其自身的优点及可解决多维证券定价的特点,将成为此类金融产品定价发展的趋势所在。本文即提出使用蒙特卡罗模拟技术对贷款中的隐含期权进行定价,利用仿真的方法模拟出在不同的利率水平下的各期权的实际价值。
二、可提前偿付存贷款的执行边界分析
(一)定期存款中隐含期权的执行边界分析
将定期存款中的隐含期权视为一种美式期权,具有很强的期权特性[6]。投资者在到期日之前都可以执行此期权使自己的收益最大化,因此有必要对投资者何时行使该期权进行界定。如存款者在0时刻跟银行签订了一个T年期定期存款合约,合约的利率为R0,T,活期利率为h0,T。若始终维持此合约,则到期时的本利和为eR0,TT(采用复利计算)。若在t时刻,银行突然宣布上调利率至Rt,T,假设投资者的投资期间不变,为0-T,投资者的投资目标是要使期间的收益最大化。
则维持该存款合约的到期本息和会超过在t时刻提前支取并签订另一合约所获得的本息和,因此存款人会选择维持该合同。
则表明在t时刻提前支取,获得0至t时刻的活期存款利息与本金,并重新签订0—T年期的定期存款,在0至T时刻所得的本金与利息和大于按0时刻的利率计算的本息和,则为使自己的收益最大化,该存款人会选择提前支取并转存。
将以上两种情况相结合,在t时刻,投资者在T期末总收益可以表示为:

所以该期权的执行条件为:

期权的执行价格为:eR0,T*T。该期权表示一个利率看涨期权,其中eR0,T*T表示0-T内不含期权的贷款利率本利和。在期权执行之后,借款人可重新申请一个期限为T-t的贷款,自然又获得了一个期权,即在 T-t期间又可以进行提前支取并按新利率签订新合同,此时的执行价格为eRt,T(T-t)。因此对于存款人来说,一个定期贷款可以分解为一个基本的债权和若干个美式看涨期权,此期权的执行与否,完全取决于存款利率的变化。
(二)可提前偿还贷款中隐含期权的执行边界分析
假设当期一个投资者同银行签订一份期限为T的贷款合同,连续复利贷款利率为r0,T,贷款金额简化为1,违约金为α,假设贷款人贷款期间不变为0-T。如果贷款者没有提前偿还贷款,则其总成本为er0,T*T(为简化起见,假设贷款为到期一次性偿还)。如果在时刻t,市场利率突然发生改变,则在余下的时间T-t,新的贷款利率表示为:rt,T。
则维持该项贷款的到期本利和会超过在t时刻提前偿还的本利与违约金两项之和按照新利率计算的到期本利和。因此贷款人会选择提前偿还贷款,缴纳违约金,并按新利率rt,T申请本金为T-t的新贷款。
则维持原有定期贷款的成本低于提前偿还,缴纳违约金并两项金额重新签订新贷款的总成本,借款人会维持原有贷款合同不变。
将以上两种情况相结合,在t时刻,借款人贷款期末总成本可以表示为:
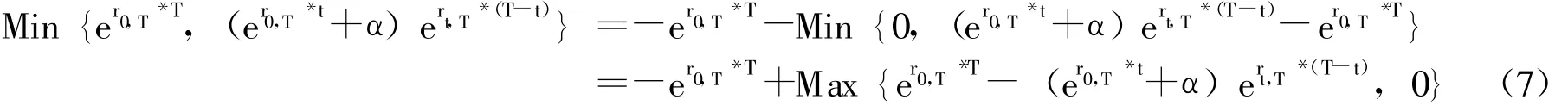
所以该期权的执行条件为:

三、银行期权定价的蒙特卡罗模拟过程
利率的动态特征对于利率的预测及相关衍生产品的定价具有重要意义,因此对利率模型的估计也提出了许多不同的方法,其中以极大似然法 (MLE)和广义矩估计法 (GMM)的理论研究和实证支持最具代表性,其中已有文献证明,对于复杂利率模型的估计,MLE方法的精确性优于GMM方法[7],故本文拟采用MLE方法对模型参数进行估计。基于模型对中国金融市场利率的适应性,同时考虑到模型估计的便利性,本文使用CIR模型,并在此模型中加入跳跃项,表示市场的突发事件(如政策的突变、股市崩盘等)对利率过程带来的影响。
CIR模型认为,在风险中性世界中,短期利率的变化过程遵从:

其中,r表示短期瞬时利率,k表示利率均值回复速度,θ表示长期均值,σ表示波动率。在本论文中,我们在该短期利率变化中加入跳跃项,即单因子瞬时短期利率均值回归漂移——跳跃模型,可以表示为:

其中k表示向均值调整的速度,u(t)表示时刻t的利率长期均值,σ(t)则表示波动率,W(t)代表布朗运动。J代表服从某些分布的随机变量,为避免突发的深度跳跃使利率出现负值情况,我们这里假设J服从 (a,b)的均值分布,dP则代表强度为λ的泊松分布。
关于模型的参数估计,可以参看刘凤琴等 (2009)关于参数估计及其蒙特卡罗检验[8]。本文在此主要分析其价格的蒙特卡罗估计过程。
(一)蒙特卡罗模拟过程的基本步骤
蒙特卡罗模拟的实质是通过随机抽样的样本均值来近似代替随机分布的总体期望值,从而得到对随机分布数学期望的实际估计的数值分析方法。蒙特卡罗模拟就是通过模拟这些数学期望或积分来估计标的变量的[9],其步骤如下:
1.风险中性测度下模拟出标的变量在有效期内的样本路径
在前文分析的理论基础上,我们在CIR模型中加入跳跃项J,使之更符合实际情况中利率的不连续变动,即有:

将此模型用离散化进行模拟,取△t=1个月,模拟在当前初始利率状态下,经过5年即60个月的时间后,利率可能经过的路径,重复利用此模拟方法,可以模拟此利率路径图。
2.各样本模拟路径上的隐含期权价值的计算
根据该利率变动的特点,在每一条利率样本路径上均可能涉及到存款的提前支取情况,因此在一条路径中可能存在多个期权执行情况,但基于美式期权执行的最优策略问题,其间只存在一个最佳执行点,则此最佳执行策略时的期权值的贴现值即为该条模拟上隐含期权的期权值。即期权值为:

其中,C为期权的价值,r为无风险利率,X为此存款未被提前执行时的利息总和,ST为存款进行转存后所得的最大利息和。
3.对所模拟出的样本路径上的相应期权值求平均值
对所模拟出的样本路径上相应期权值求平均值,得到此定期存款中隐含期权估计值。即:

(二)对偶变量方差减少技术应用
按传统的蒙特卡罗模拟方法进行,需要很大的次数N值,才能得到满足精度要求的隐含期权c的估计值,这将消耗大量的计算时间,为了使这种方法更具有适用性,即减少计算量和缩小误差,提出了很多优化方法:如对偶变量技术、控制变量技术、重点抽样法、时刻匹配法等。本文使用对偶变量技术,该方法的实质是:每次模拟运算期权价值的两个值,第一个C1通过正常方法得到,第二个C2是通过改变抽样样本的符号计算出来的 (如果ε是用来计算第一个期权值的样本,则-ε用来计算第二个值的样本)。由该模拟运算得出的期权价值是这两个计算值的平均值[10]。将对偶变量法引入蒙特卡罗模拟的步骤是:
(1)风险中性概率测度下模拟出标的变量Y在衍生证券有效期内的样本路径,并采取相同的随机变量生成标的变量X在衍生证券有效期内的样本路径,即Y的利率路径为:

其中dwt值是通过 ti-ti-1Z即 ΔtZ来模拟,Z~N(0,1)服从正态分布;J服从均值为 (a,b)的均值分布,dP为强度λ的泊松分布,也是通过随机抽样来抽取。因此,假设在一次利率模拟中dwt的抽样值为a,Jdp的抽样值为b,则变量X的利率路径可表示为:
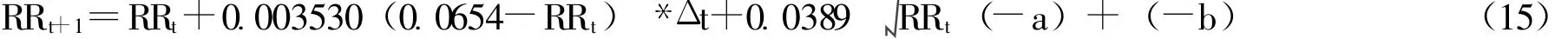
(2)根据该衍生证券的性质,估计出第i条样本路径上的基于利率RR的X隐含期权与基于利率R的Y存款隐含期权的贴现盈利收益;
(3)对所模拟出来的X与Y样本收益上盈利收益求平均,得到该衍生证券的估计值。
四、实证模拟
(一)案例描述及实施过程
在这里我们选择定期存款隐含期权为研究对象加以分析。以2007年11月21日公布的五年期存款利率0.0585为初始利率,计算从该时期开始的五年期存款中的隐含期权值。贴现利率取一年期定期存款利率值:0.0414。为了计算定期存款中隐含期权的价格,我们可以根据前面估计出来的参数模拟出未来存款利率的变动,并计算每次利率变动路径下的期权收益,最后求出收益的均值并按照原先利率进行贴现,就可以得到隐含期权的价格[7]。根据央行2007年11月21日对人民币利率的调整,现行的存款基准利率分别为:

表1 2007年11月21日央行公布的存款基准利率
(二)蒙特卡罗模拟方法估计期权价值的步骤
1.利率路径的模拟
根据前述参数估计方法,我们可以得出参数值的取值为:
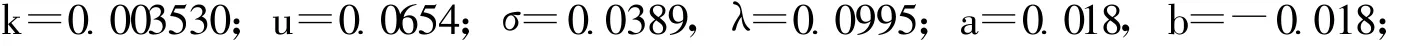
则此定期存款利率的跳跃扩散模型离散化公式为:
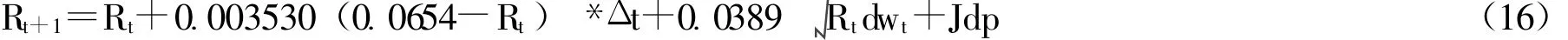
Rt取现存的五年期定期存款利率 0.0585;△t以月为单位,即1/12;布朗运动 dwt可用来模拟,其中Z~N(0,1)正态分布,可在Matlab里实现标准正态分布的样本抽样;J服从均值为 (-0.018,0.018)的均值分布,dP为强度λ为0.0995的泊松分布,均通过Matlab中命令的识别抽样完成。
2.计算出在期权被执行时的价值

若此客户选择在t时刻提前支取存单,在t时刻的利率水平为rt,T=rt,60,活期存款利率为h0,T,则其再存款的利息之和为则其选择提前支取存款并以另一利率转存的前提条件是:初始存款总收益小于转存后利息总收此式中的t即为理性的提前偿付日期。期权的价值为:C=e-rtmax(ST-X,0)。另外,考虑美式期权的最优执行策略问题,在一条利率模拟路径上,使期权值最大的时间点作为执行期权的时间点,再将此值用时间价值进行贴现,即可得出此期权的价值。如此根据利率的一次模拟,即可形成一次存款及其提前支取行为。
图1是模拟10000次的过程中,各条路径上相应的隐含期权值。由此可见,在10000次的运行中,定期存款中的隐含期权执行与否是随着利率模拟路径的变化而变化的,在有些利率路径变化过程中,不执行期权为宜,而在有些利率路径图中,执行期权是明智的选择。
3.对所模拟出的样本路径上的相应期权值求平均值
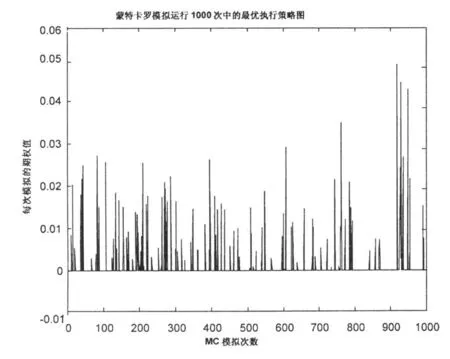
图1 5年期定期存款中隐含期权的被执行情况模拟
根据大数定理,将模拟运行多次(5000次以上),运行结果的平均值即为所求值。并分别通过模拟1000次、2000次、5000次、10000,分析其收敛情况如图2。
由上图2可看出,该隐含期权值在模拟运行2000次以内时,期权的波动较大,且并不稳定,而大约在运行3000次后一直到10000次,期权值渐渐趋于稳定,最后的期权值为0.0015。模拟运行后,期权值的估计值趋向于平稳,得出此估计值为:c=0.0015;即5年以上利率为0.0585的定期存款,存款期限为5年时,其隐含期权的价值为0.15%。即根据无套利定价理论,商业银行的5年期存款利率应为:原存款利率-隐含期权价格:0.0585-0.0015=0.0570。
(三)对偶变量技术应用
从图2中可以看出,蒙特卡罗模拟明显的不足就是对于一些复杂的衍生证券,为得到精确的结果,需要进行很多的模拟次数,否则将产生较大的估计方差。如上例中,需要运行程序大约3000次才真正得以收敛。根据对偶变量技术原理,我们对蒙特卡罗模拟方法进行改进,得到其稳定性能图,将其与传统蒙特卡罗模拟方法进行比较如下:
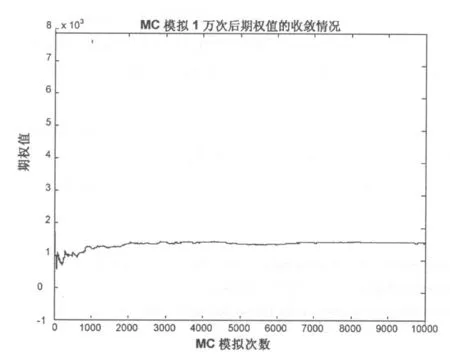
图2 MC模拟1000、2000、5000、10000次的期权值收敛情况
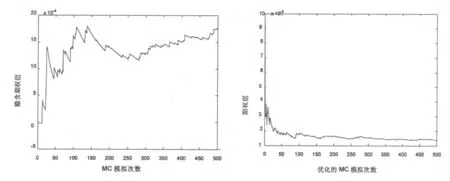
图3 传统的MC方法与优化的MC方法分别运行5000次得出期权值的波动比较
其中,图3中左图是传统的蒙特卡罗模拟运行5000次的情况,右图是加入对偶变量技术的蒙特卡罗模拟运行5000次的情况。由此可以比较得出,加入方差减少技术的蒙特卡罗模拟方法,其收敛速度大大加快,即有效克服了蒙特卡罗模拟收敛速度慢的问题。而两种模拟方法得出的期权值都是一样的,即0.0015。
五、结论分析
本文主要研究结论包括三个方面:一是可提前支取存款是一种复杂的隐含期权。对投资者而言,定期存款可以分解为一个基本债权和若干个美式看涨期权的多头;对银行而言,定期存款可以分解成一个基本债务和若干个美式看涨期权的空头。二是运用蒙特卡罗模拟能比较有效解决商业银行存款中隐含期权的定价问题,且加入方差减少技术的蒙特卡罗模拟方法可以大大降低其误差,提高其模拟收敛效率。三是在目前的利率水平和利率管制体制下,中国银行机构的存款利率相对偏高,其存款利息成本高于风险收益,存在缺口。
由于本文研究内容具有很大的复杂性和综合性,而且研究的领域也比较新,隐含期权理论还不是很成熟,有些观点与国内外学者还未达成一致,所以给本文的研究带来一定的困难,对存贷款中隐含期权的应用研究存在许多不足,还处于起步阶段,有很多的问题有待进一步研究和探讨。
[1]Brent W.,Richard J.,Embedded.Options in the Mortgage Contract[D],Working Paper,1998,Pennsylvania University.
[2]Brooks R.Computing Yields on Enchanced CDs,Financial Service Review.1996,5(1):31-42.
[3]Hatem Ben-Ameur,Michele Breton,Lotfi Karoui.A Dynamic Programming Approach for Pricing Options Embedded in Bonds[J],Journal of Economic Dynamics&Control.2006
[4]郑振龙,林海.银行资产负债中隐含期权的定价[J].金融研究,2004,(7).
[5]夏和平,周茂彬,王小明.存贷款业务中的隐含期权对我国商业银行利率风险的影响 [J],金融研究,2007,(9):138-150.
[6]刘畅,徐承龙,谢志华.提前还贷及其隐含期权的分析[J],应用数学与计算数学学报,2006,(12):25-30.
[7]Longstaff,F.A,Schwartz,E.S.Valuing American Options by Simulation:Simple Least squaresapproach[J],Review of Financial Studies,2001,14(1):113-147.
[8]刘凤琴,戈晓菲.利率跳跃扩散模型的理论估计与蒙特卡罗模拟检验 [J].管理工程学报,2009,(4):91-96.
[9]马俊海.金融衍生证券定价的数值分析方法 [M]:浙江人民出版社,2002.97-101.
[10]Paul Glasserman.Monte Carlo Methods in Financial Engineering[M],高等教育出版社 (影印版)2008.

