ANALYTIC SOLUTION FOR WAVE DIFFRACTION OF A SUBMERGED HOLLOW SPHERE WITH AN OPENING HOLE*

DONG Man-sheng

State Key Laboratory of Ocean Engineering, Shanghai Jiao Tong University, Shanghai 200030, China, E-mail: dongms@sjtu.edu.cn

School of Civil Engineering, Hefei University of Technology, Hefei 230009, China

MIAO Guo-ping, ZHU Ren-chuan, FAN Ju

State Key Laboratory of Ocean Engineering, Shanghai Jiao Tong University, Shanghai 200030, China

ANALYTIC SOLUTION FOR WAVE DIFFRACTION OF A SUBMERGED HOLLOW SPHERE WITH AN OPENING HOLE*

DONG Man-sheng

State Key Laboratory of Ocean Engineering, Shanghai Jiao Tong University, Shanghai 200030, China, E-mail: dongms@sjtu.edu.cn

School of Civil Engineering, Hefei University of Technology, Hefei 230009, China

MIAO Guo-ping, ZHU Ren-chuan, FAN Ju

State Key Laboratory of Ocean Engineering, Shanghai Jiao Tong University, Shanghai 200030, China

An investigation is carried out on the interaction of surface waves with a submerged sphere having an opening hole in finite-depth water in this article. Based on the linear wave theory, the method of multipole expansions is used to obtain the fluid velocity potential in the form of double series of the associated Legendre functions with the unknown coefficients of an infinite set. In terms of the body surface boundary condition and the matching condition between the inner and outer flows at the hole, the complex matrix equations for the coefficients of the series are established. The infinite sets of matrix equations are solved by truncating the series at a finite number. The hydrodynamic pressure on the structure surface and the exciting forces acting on the structure are graphically presented. The dynamic pressure on the wave front surface of the sphere varies slightly with angle of opening hole increasing, while that on the wave back surface does obviously. When the angles of opening hole are increasing, the absolute values of the complex exciting forces tend to fall as a whole.

diffraction, surface waves, submerged sphere, multipole potential

1. Introduction

Due to extensive applications to the offshore and ocean industries, there has been a mass of work on the interaction of a sphere with waves. There are predominantly two kinds of methods to solve theseissues theoretically, i.e., the method of multipole expansions and the method of integral equations. The method of multipole expansions is based on a one-parameter family of solutions of the boundary value problem[1-3], which consists of two terms of a singular solution of the Laplace equation and integral component. The integral-equation method is based on Green’s function, which uses series and integral representations for Green’s function.

Thorne[4]introduced the method of multipole expansions for both spherical and cylindrical structures in finite and infinite depths. Wang[5], using the multipole expansions of Thorne, investigated the radiation and diffraction problems for submerged spherical vehicles, and discussed their free motions and different metacentric heights in infinite-depthwater. Linton[1]worked on the radiation and diffraction of water waves by a submerged sphere in finite-depth water with the multipole method, and predicted the free surface elevation in the vicinity of the sphere. Wu et al.[6], with the multipole expansions, investigated the exciting forces acting on a water and presented a solution for wave induced drift forces based on the linear potential theory. The combination of curvilinear coordinates and Integral Transform (IT) was used to obtain an asymptotic representation for the diffraction field near a sphere in infinite water depth by Dorfmann[7]. Using the generalized integral transforms, Dorfmann et al.[8]constructed two spectral systems and introduced two spectral functions to obtain the solution for Diffraction Problem (DP).

Besides two kinds of methods, there are other methods for this problem, such as numerical methods[9-12], eigenfunction expansions[13]and panel method[14]. For DP, specially two-dimesional DP, numerical methods are popularly used. Wang at el.[9]investigated numerically viscous flow past a rotating sphere by solving the three-dimensional Navier-Stokes equations using the finite element method. They were focused on the character of flow in the near wake.

For some reasons, in some specific areas the spherical structure may not be a whole sphere, but with an opening hole. According to the existing literature, the authors have not found an investigation on diffraction of waves by a sphere with an opening hole.

In this article, an analytical procedure for the diffraction of surface waves by a submerged sphere with an opening hole is presented. The flow potential is expanded in terms of an infinite series of the associated Legendre functions with unknown coefficients. Using the body surface boundary condition and matching the inner flow and the outside flow at the hole, we set up the complex matrix equations for the coefficients of the series. By solving these equations, we obtain unknown coefficients, the velocity potential, and consequently the exciting forces.

2. Formulation of the problem

2.1Elementary formula

It is assumed that the fluid is homogeneous, inviscid and incompressible and the fluid motion is irrotational. A surface wave with the frequencyσand small amplitudeAis applied on a hollow sphere of the radiusasubmerged in water of the finite depthd. The wave is parallel to thex-axis at the time of the incidence on the sphere and is propagating along the positivex-direction.

Two sets of coordinate systems are taken. One is a right-handed Cartesian coordinate system (x,y,z), in which thexyplane coincides with the undisturbed free surface and thez-axis is taken vertically downwards from the free surface . The geometric centre of the sphere is located at the point (0,0,h). The other set is the spherical coordinate system (r,θ,ψ) with the origin at the geometric centre of the sphere. Figure 1 shows the brief sketch of geometry for the problem.

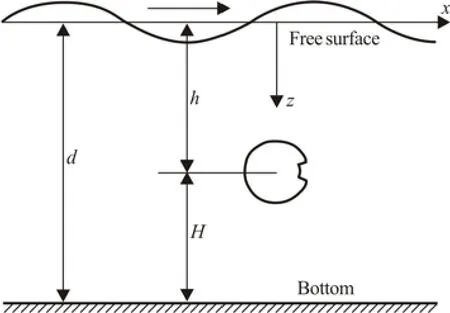
Fig.1 Sketch of geometry for the problem

The relationship between the coordinate systems is given by

It is assumed that a rectangular opening hole is situated at the wave back surface of the sphere. The longitudinal range of angle is −ψh≤ψ≤ψh, and the latitudinal range of angle is π/2−θh≤θ≤π/2+θh.

For an incompressible and inviscid fluid, and for the small amplitude wave theory with irrotationalmotion, a velocity potentialΦ(r,θ,ψ,t)can describe the fluid motion, written as

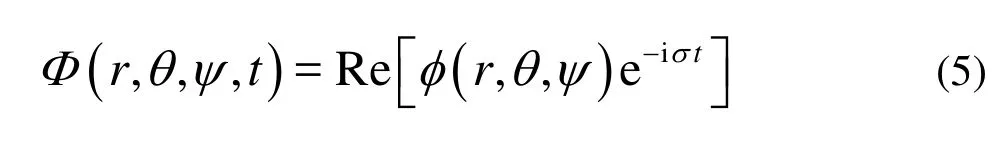
where Re stands for the real part,φis a time independent potential andσis the wave frequency.

Bernoulli’s equation gives the hydrodynamic pressureP(r,θ,ψ,t)as

2.2Velocity potential outside the sphere

The velocity potentialφoutside the sphere can be decomposed into the incident potentialφ1and the diffraction potentialφD. Thusφcan be written asφ=φI+φD. The time-independent pressurepcan be presented as a sum of the incident pressurepIand the diffraction pressurepD, i.e.,p=pI+pD.

To obtain the velocity potentialφ, the following boundary value problem is to be solved

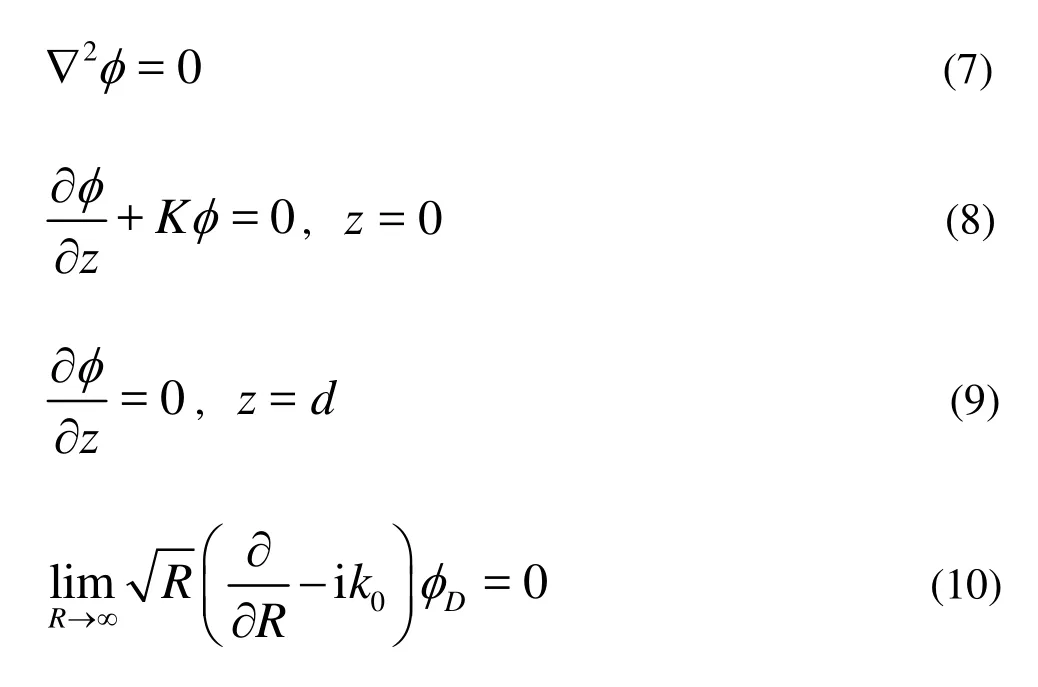
whereK=σ2/gandk0is the finite-depth wave-number defined by the dispersion relation

The diffraction potential must satisfy the body surface boundary condition

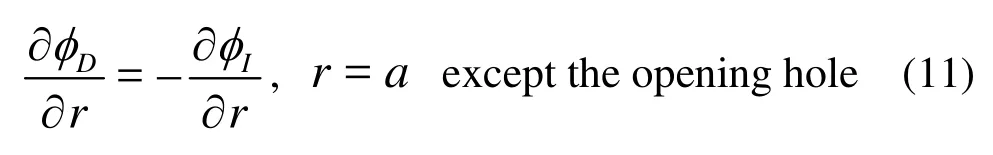
2.3Velocity potential inside the sphere

The velocity potential inside the sphere is denoted byφinner. Governing equation reads

The inner velocity potential must satisfy the inner surface boundary condition

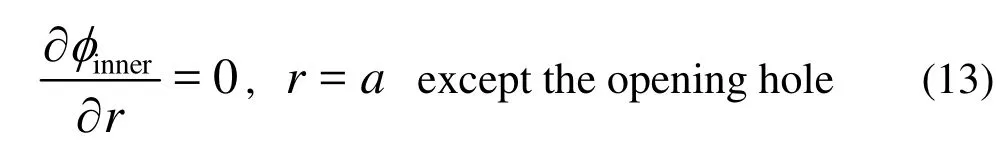
The matching condition of the outside flow field and the inner flow field reads

They can be further written as

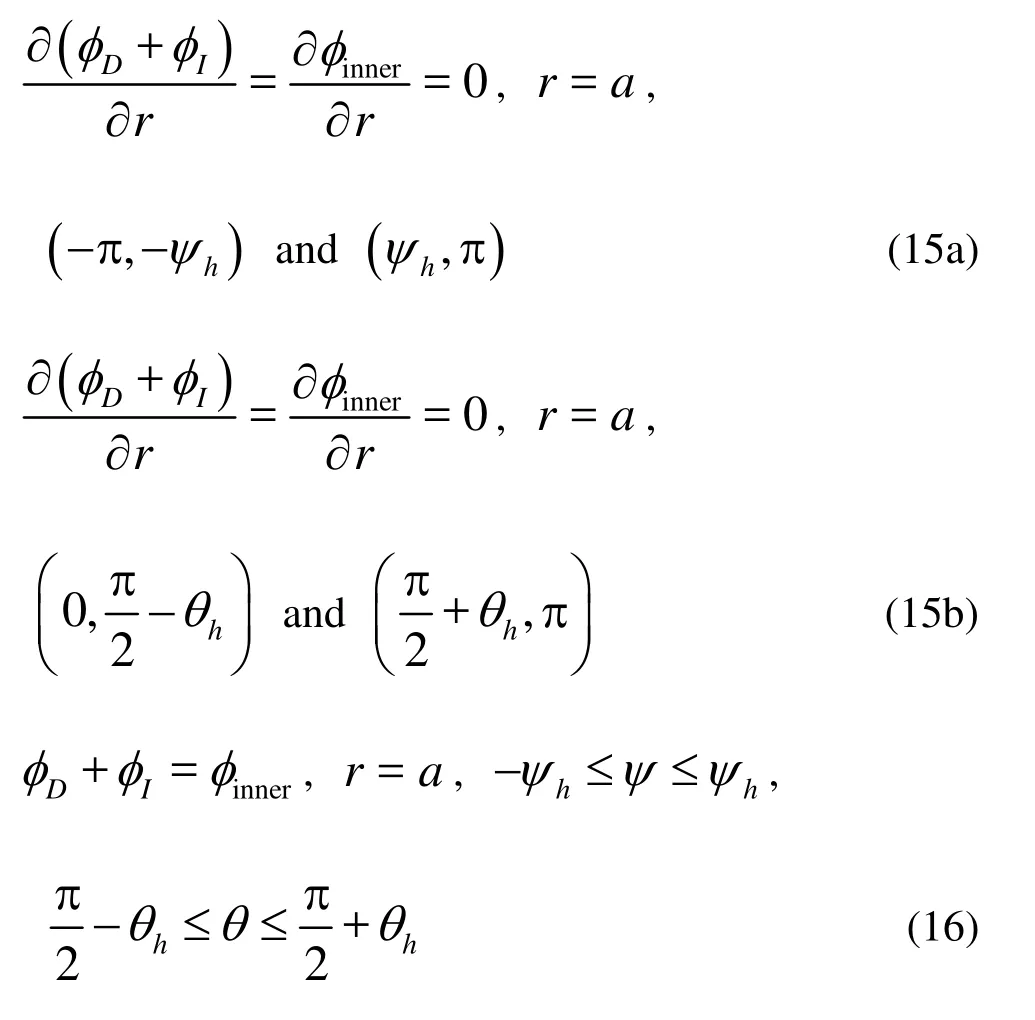
3. Multipole expansions

3.1The inner potentialBy using the method of separation of variables,the inner velocity potentialφinnercan be expressed as

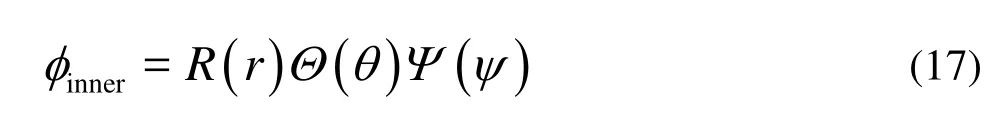
Using separation of variables for Eq.(12) we can obtain the inner velocity potentialφinner

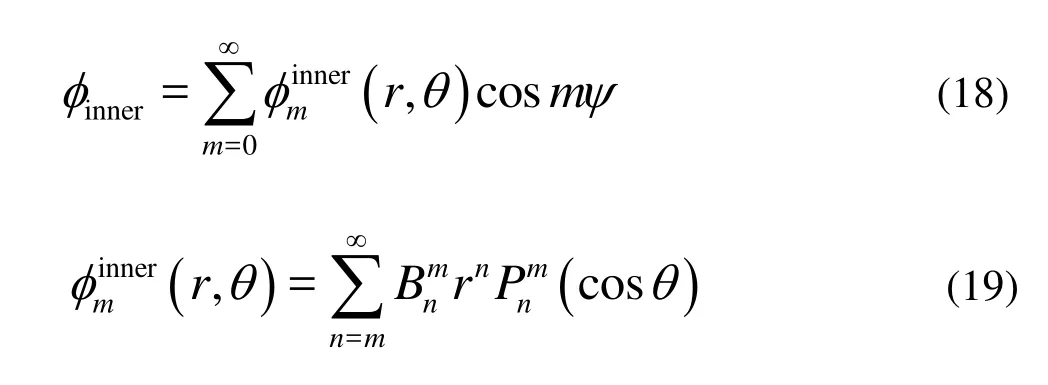
We take the first derivative ofφinnerwith respect torand have

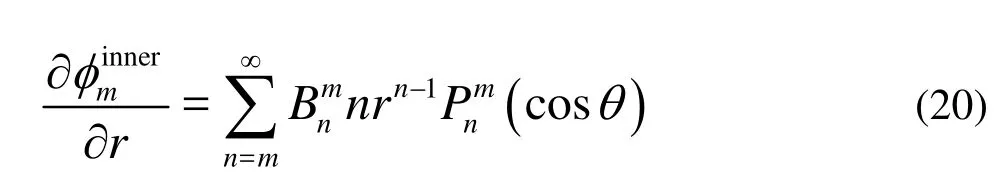
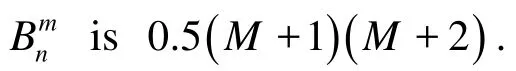
3.2Outer potential

The incoming wave with the amplitudeAand frequencyσ, propagating in the positivex-direction, can be expressed by the incident velocity potential

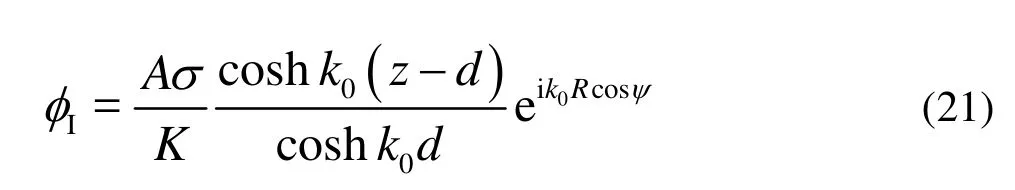
According to Linton[1]and Rahmann[2], the incident potential can be expressed in terms of the associated Legendre function as

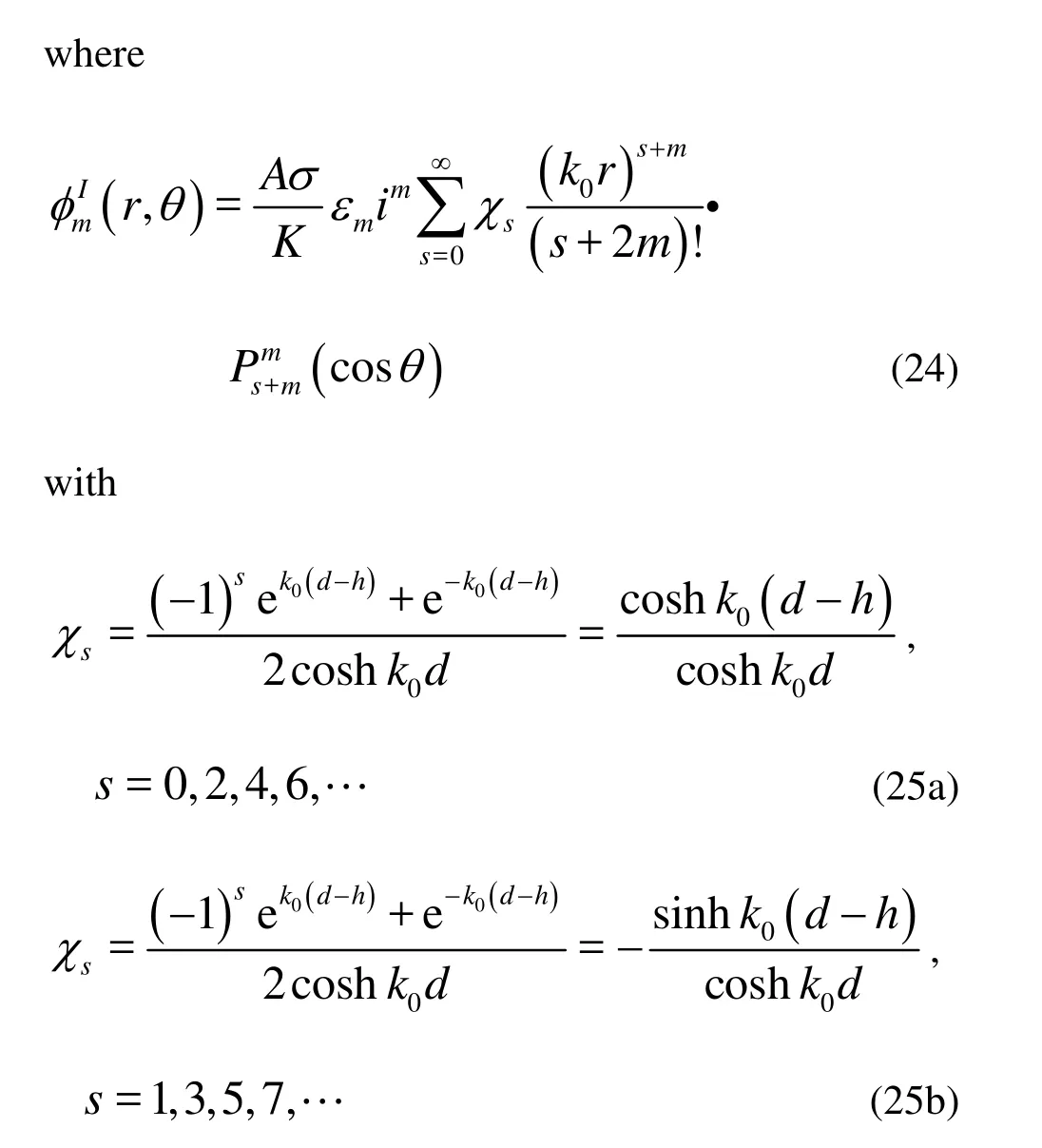
The diffraction velocity potentialDφmust satisfy Eqs.(15) and (16). We can express this potential as

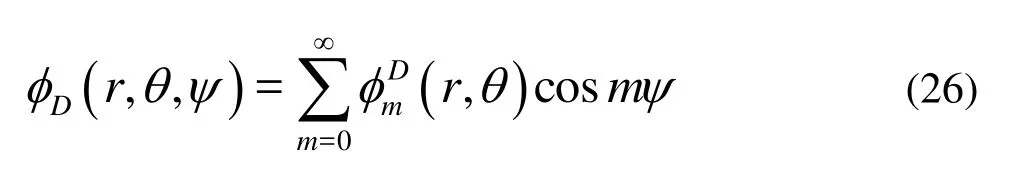
where theψ-independent potential is

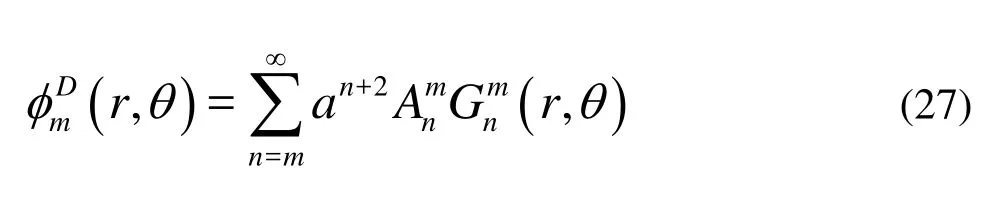
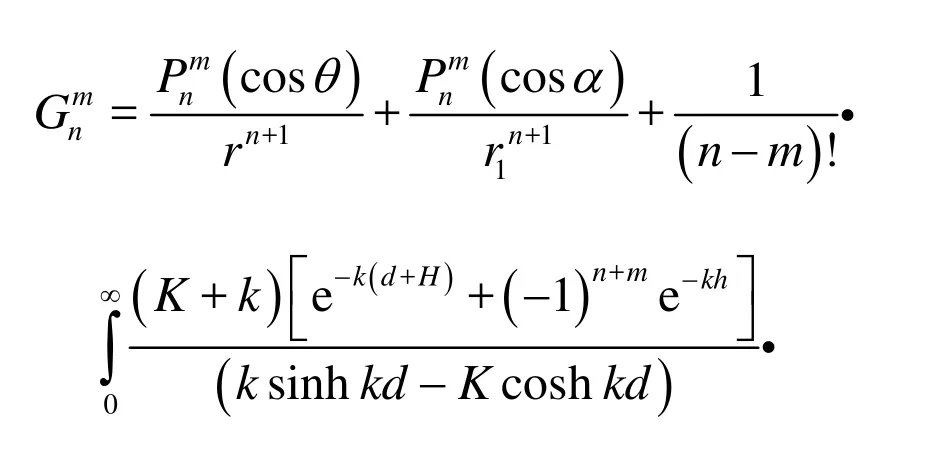
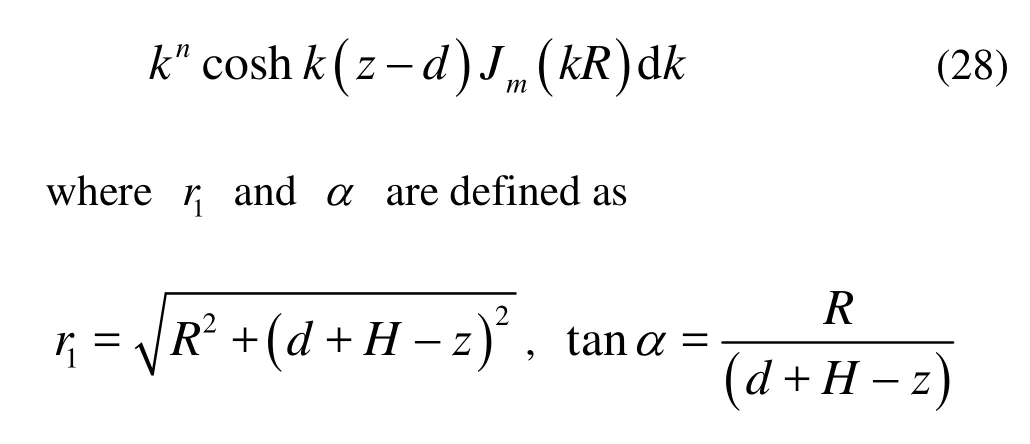
The line of integration in Eq.(28) passes under the singular point of the integrand atk=k0.

The second and third terms in Eq.(28) can be expanded into a series of the associated Legendre functions by

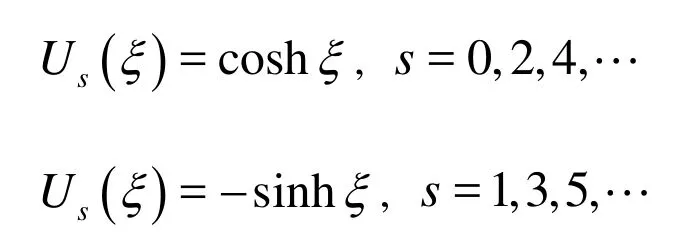
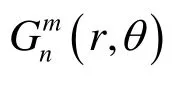
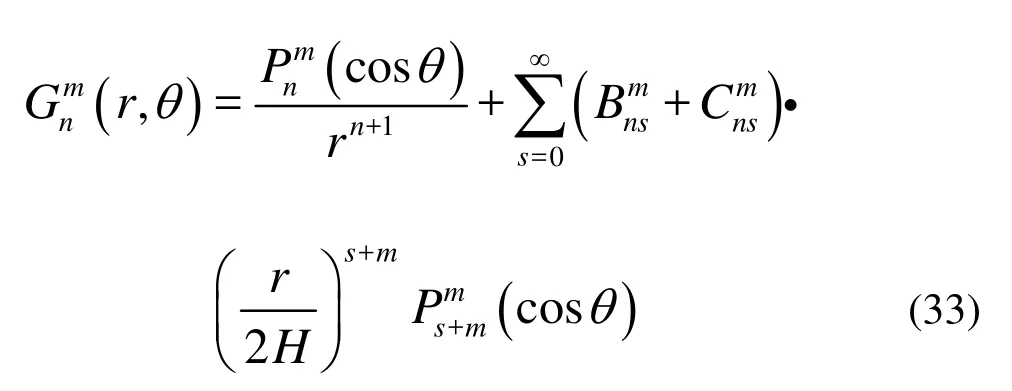
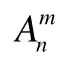
3.3Matching the inner and outer flow fields

There are two matching conditions for the hollow sphere surface, including the opening hole. In other words, the velocity potentials satisfy both the body surface condition and the opening hole condition, i.e., Eqs.(14) and (34).

On the hollow sphere wall surface, both sides of Eq.(14) are equal to zero, which are satisfied by functions introduced below. At the opening hole, the normal derivatives of the inner and outer field potentials are equal.

Further we define a functionG

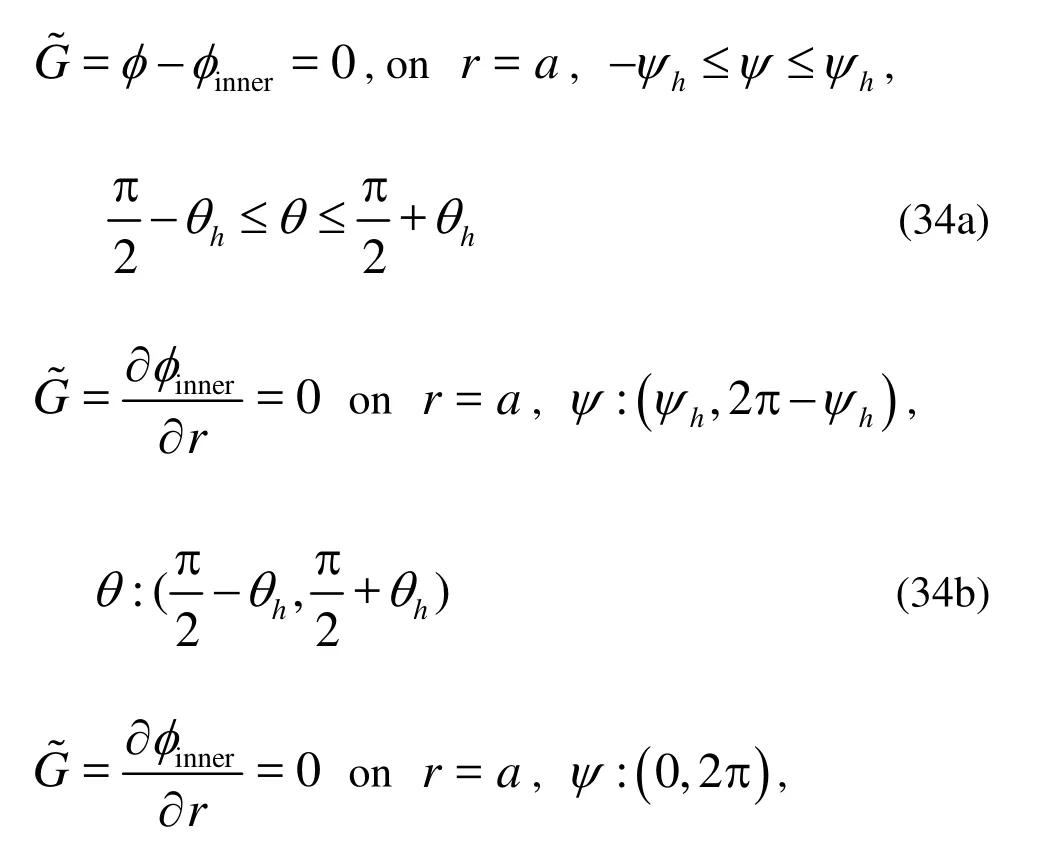
According to the matching condition of Eq.(14), we have

The associated Legendre functions have orthogonality relationships, when θ is in the range from 0 to π. Then we can obtain

and δnsis the Kronecker delta function.

We discompose the sphere surface into three sections (0,π/2−θh), (π/2−θh,π/2+θh) and (π/2+θh,π)in the latitude direction. The opening hole is at (π/2−θh,π/2+θh). The boundary of (0,π/2−θh)and (π/2+θh,π)is wall boundary. According to the matching condition of Eq.(34), we have

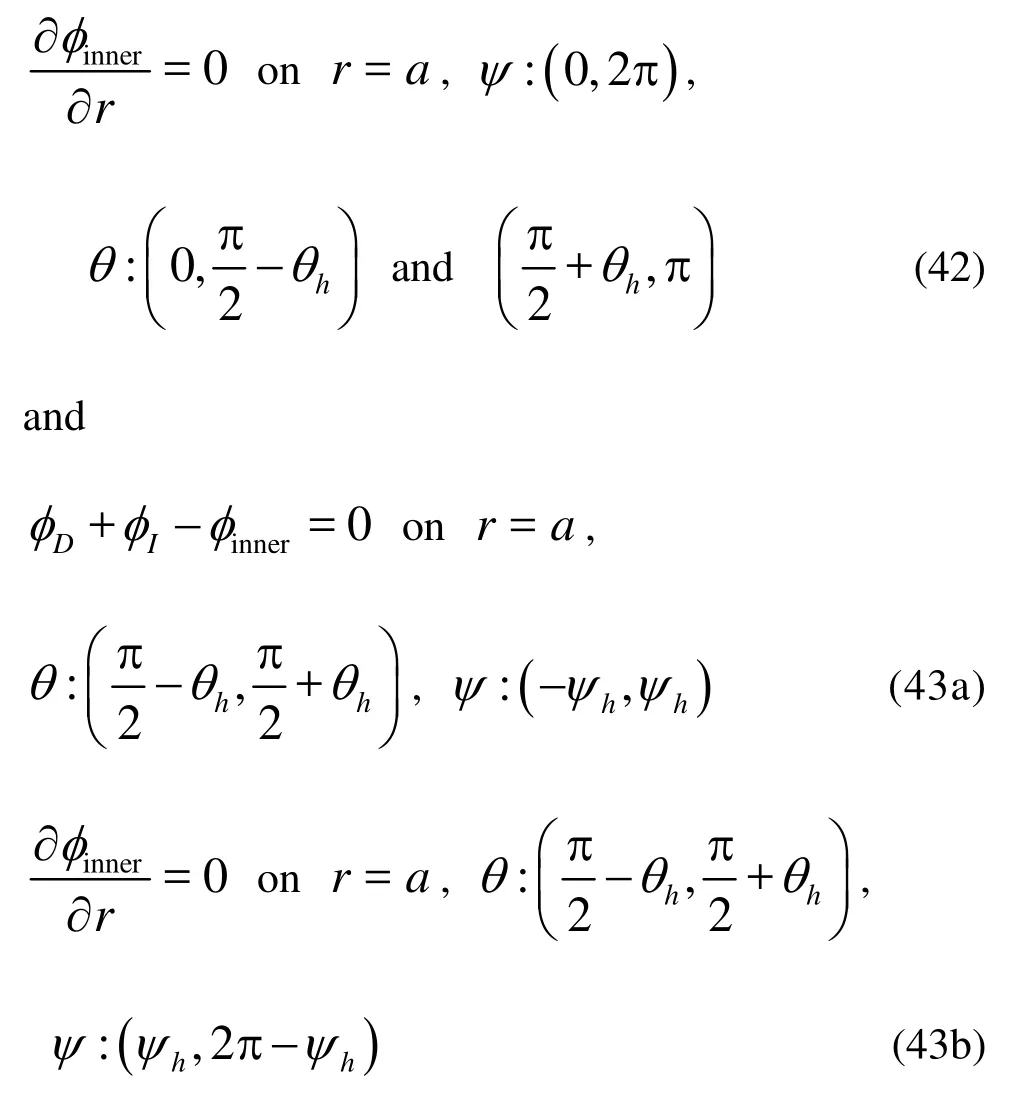
Equations (42) and (43) are multiplied by coskψ, and integrated from 0 to 2π. According to the orthogonality properties ofmψcosine functions at the extent (0,2π), noticing Eqs.(18), (19), (20), (23), (24), (26), (27) and (33), we have

回到村路上，没买到米的牛皮糖步子越走越慢。眼皮耷拉着，目光不离脚尖，寻着路走，好像丢了钱。看看走到自家的八斗丘旁，牛皮糖忽然中了邪，眼睛一亮，手舞足蹈起来。后来就跨过那条两尺高的田埂，跳到了八斗大田中，蹲了下来。五月的大田里空空荡荡，零星的苜蓿花瘦弱地开放着。这里那里的硬土上开着坼，像无数条蚂蝗巴在饱经沧桑的皮肤上。一条污渍斑斑的水沟，从猴头岭上的工业园下来，巨蟒一般越过八斗丘，拐进旁边一条水渠，扭向洞庭湖。牛皮糖从不抽烟，他蹲在那里没有事干，就只是专注地盯着那条沟，一动不动，把一种心事涂抹在迷蒙的田野上，很久。

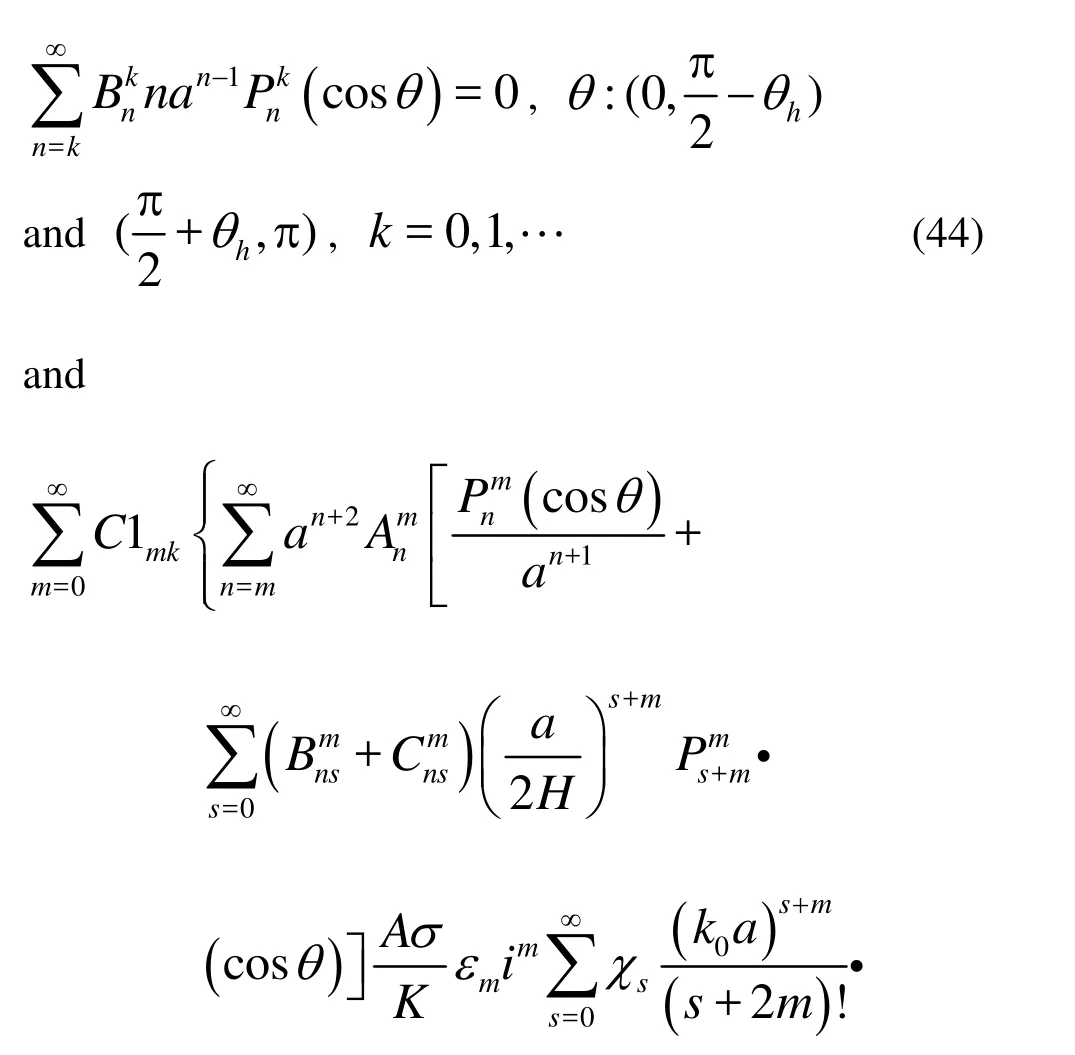
In terms of the orthogonality of the associated Legendre polynomials in theθinterval of 0 to π, Eqs.(44) and (45) are multiplied by(cosθ)sinθand integrated forθover the interval [0,π]. Noticing the definition extent of these equations, we define

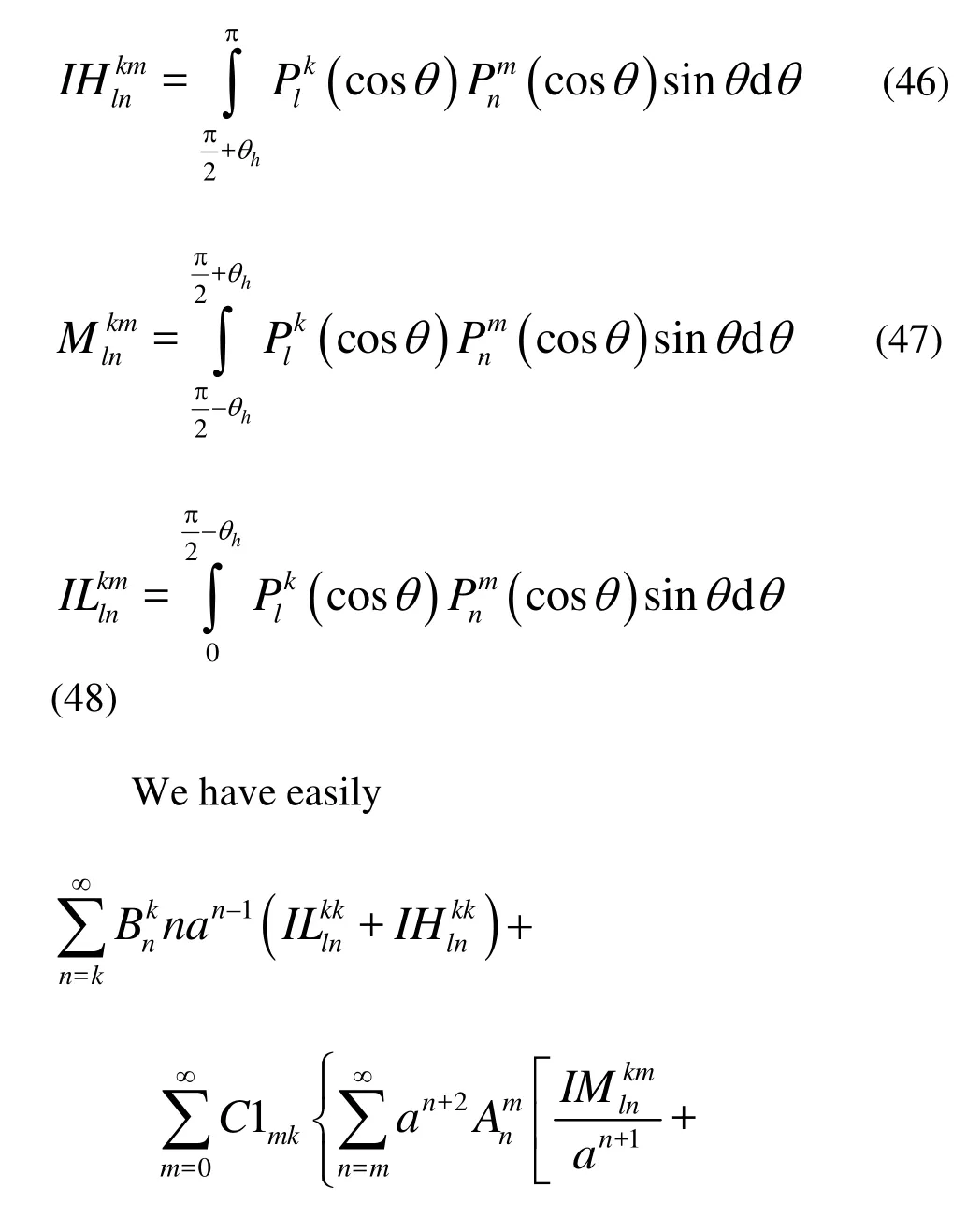
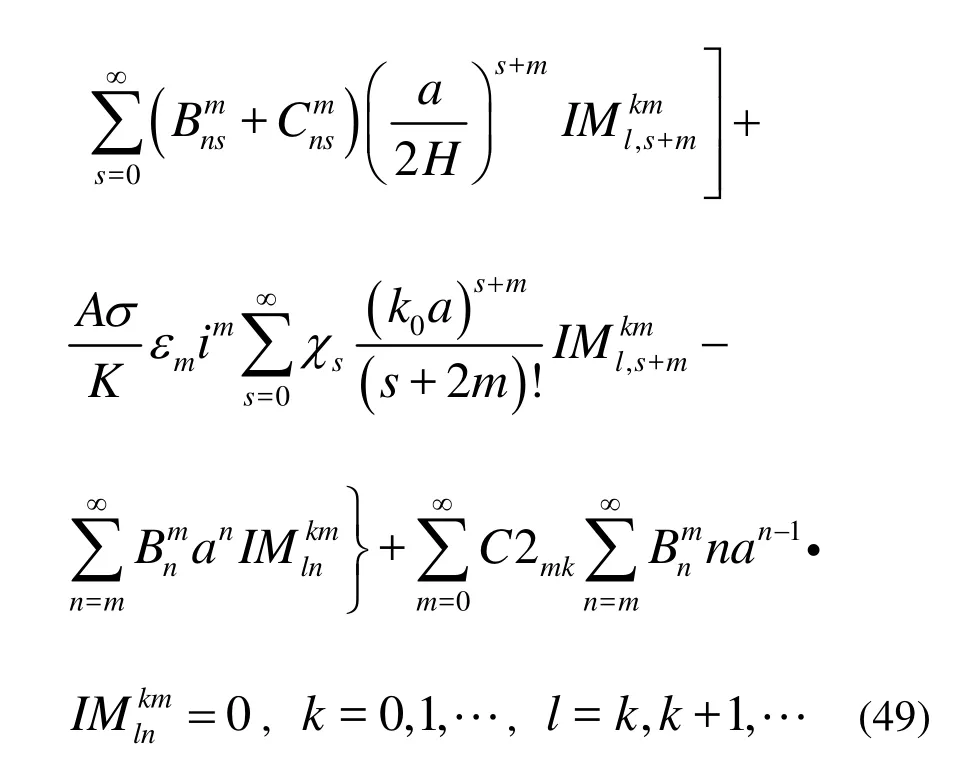
Equation (49) is similar to Eq.(37) in unknowns. Ifkis truncated toM, there are 0.5(M+1)(M+2) linear equations with unknown coefficientsand. Thus there are (M+1)(M+2) linear equations with unknown coefficientsandfor Eqs.(37) and (49). Obviously, the number of unknown coefficients is also (M+1)(M+2). Through solving these equations we can determine the unknownsandand accordingly obtain the inner and outer velocity potentials.

4. Exciting forces

The total exciting forces on the sphere by the incident and diffraction potentials can be calculated by integrating the total pressurePover the body surfaceΩ

Herenis the normal vector out of the body surface having the components

nx=sinθcosψ,ny=sinθsinψandnz=cosθ

5. Numerical computation

The rapid convergence of the infinite seriessolutions in terms of the associated Legendre functions has been found with respect to the diffraction parameterKa. So we can solve the infinite equations by truncating the series at a finite numbern=N. Rahman[2]indicated thatN=5 gave the accuracy to four significant digits. In this articleN=4 was taken to make numerical computation.

Fig.2 Theopressure on the wave front surface of the sphere at 180 in the logitudinal direction due to diffraction of the incident wave Ka=0.5, h/ a=2, d/ a=5 and t=0

Numerical analysis was conducted to observe the distribution of the dynamic pressure on the sphere surface and the relationship between wave-exciting forces on the structure and angles of opening hole. Main parameters of numerical simulation are as follows:a=3, the submergence parameterh/a=2, the depth parameterd/a=5, the wave amplitude parameterA/a=0.15, and opening hole angles from 0 to 0.4 at interval 0.1 for wave-exciting forces and 0, 0.1, 0.3, 0.5 for the dynamic pressure.

Fig.3 The pressure on the wave back surface of the sphere at 0oin the logitudinal direction due to diffraction of the incident wave Ka=0.5, h/ a=2, d/ a=5 and t=0

Figures 2 and 3 show the dynamic pressure on thesphere surface at angles of 0oand 180oin the longitudinal direction due to diffaction of incident waveKa=0.5,h/a=2,d/a=5 andt=0, respectively. We can see that the dynamic pressure on the wave front surface of the sphere, i.e., at longitudinal 180o, varies slightly with the opening hole angles increasing, while that on the wave back surface, i.e., at longitudinal 0o, does obviously and the hydrodynamic pressure changing is weak.

Due to the symmetry of the problem we immediately haveFy=0. Figure 4 shows the absolute values of the complex exciting forcesFxandFzversus opening hole angles for the fixed submergence whenθh=ψh. We can see that the forces induced by long wave are obviously smaller than those by short wave. When angles of opening hole are increasing, the absolute values of the complex exciting forces tend to fall as a whole.

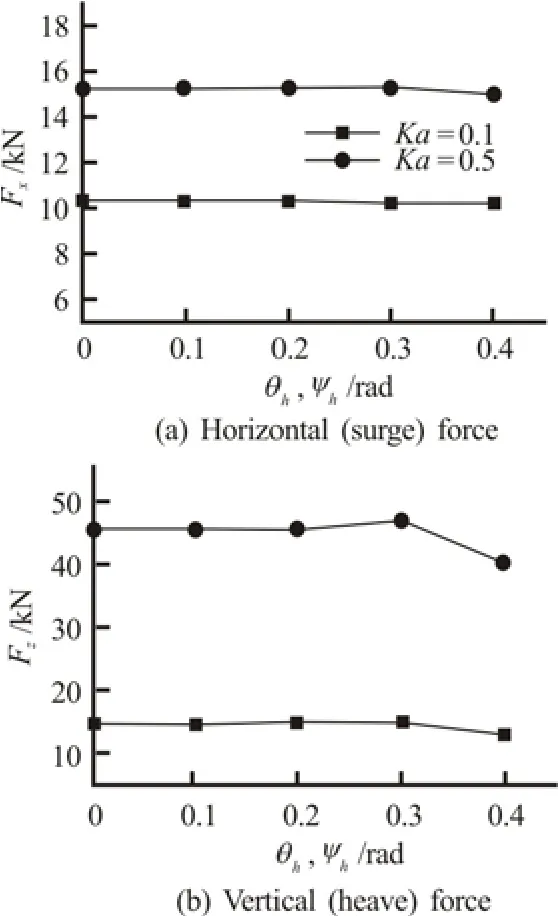
Fig.4 Absolute values of the complex exciting forcesFxandFzversusθh,ψhdue to diffraction of the incident wave,h/a=2,d/a=5

6. Conclusions

The above method in this article can be applied to optimization analysis for nonholonomic spherical structures in ocean engineering. Wang et al.[15]indicated a proper bulbous bow can significantly reduce wave-making resistance of high speed warship. We can optimize bulbous bow with a notch by the presented method. In addition, this work may serve as a benchmark to check different numerical schemes for validation.

[1] LINTON C. M. Radiation and diffraction of water waves by a submerged sphere in finite depth[J].Ocean Engineering,1991, 18(1): 61-74.

[2] RAHMAN M. Simulation of diffraction of ocean waves by a submerged sphere in finite depth[J].Applied Ocean Rasearch,2002, 23(6): 305-317.

[3] RATOCK TAYLOR R., HU C. S. Multipole expansions for wave diffraction and radiation in deep water[J].Ocean Engineering,1991, 18(3): 191-224.

[4] THORNE R. C. Multipole expansions in the theory of surface waves[J].Proceedings of Cambridge Philosophical Society,1953, 49(4): 707-716.

[5] WANG S. Motion of a spherical submarine in waves[J].Ocean Engineering,1986, 13(3): 249-271.

[6] WU G. H., WITZ J. A. and Ma Q. et al. Analysis of wave induced drift forces acting on a submerged sphere in finite water depth[J].Applied Ocean Research,1994, 16(6): 353-361.

[7] DORFMANN A. A. Diffraktion von wasserwellen an einer Kugel[J].Applied Mathematics and Mechanics,1996, 76(8): 471-478.

[8] DORFMANN A. A., SAVVIN A. A. Water waves diffraction by a submerged sphere and dual integral transforms[J].Journal of Computational and Applied Mathematics,1998, 91(1): 1-30.

[9] WANG Yan-xing, LU Xi-yun. Finite element analysis of viscous flow past a rotating sphere[J].Journal of Hydrodynamics, Ser. B,2001, 13(2): 83-88.

[10] ZHU S. P., MITCHELL L. Diffraction of ocean waves

around a hollow cylindrical shell structure[J].WaveMotion,2009, 46(1): 78-88.

[11] HU Ke-lin, DING Ping-xing. Numerical study of wave diffraction effect introduced in the SWAN model[J].China Ocean Engineering,2007, 21(3): 495-506.

[12] MARTYUSHOV S. N., MARTYUSHOVA Y. G. Numerical simulation of shock wave diffraction on the sphere in the shock tube Source[C].Numerical Analysis and Its Applications - 4th International Conference.Lozenetz Bulgaria, 2009, 408-414.

[13] SHI Qiang, YOU Yun-xiang and MIAO Guo-ping. Diffraction of water waves by a vertically floating cylinder in a two-layer fluid[J].China Ocean Engineering,22(2): 181-193.

[14] GAO Zhi-liang, ZOU Zao-jian. A three-dimensional desingularized high order panel method based on Nurbs[J].Journal of Hydrodynamics,2008, 20(2): 137-146.

[15] WANG Zhong, LU Xiao-ping. Research on high speed surface warship with bulbous bow[J].Journal of Hydrodynamics, Ser. A,2006, 21(6): 789-795(in Chinese).

November 3, 2009, Revised April 5, 2010)

* Project supported by the China Postdoctoral Science Foundation (Grant No. 20090460636), the Shanghai Postdoctoral Scientific Program (Grant No. 09R21413600), the Specialized Research Fund for the Doctoral Program of Higher Education (Grant No. 20090111120016), and the National Natural Science Foundation of China (Grant No. 50639020).

Biography:DONG Man-sheng (1973-) Male, Ph. D., Associate Professor

MIAO Guo-ping,

E-mail: gpmiao@sjtu.edu.cn

2010,22(3):295-304

10.1016/S1001-6058(09)60058-5