一种Loop细分小波的边界处理方法

赵 罡， 季宝朋， 白 杰

（北京航空航天大学机械工程及自动化学院，北京 100191）

一种Loop细分小波的边界处理方法

赵 罡， 季宝朋， 白 杰

（北京航空航天大学机械工程及自动化学院，北京 100191）

细分小波近年来发展迅速，在计算机图形显示、渐进网格传输和网格多分辨率编辑等领域获得了广泛的应用。Bertram提出的 Loop细分小波是基于提升格式的双正交细分小波的典型范例，它所针对的对象均为网格的内部顶点。目前尚未发现相关文献提及细分小波对于边界的处理。该文在Loop细分小波算法的基础上，给出了一种Loop细分小波边界处理的方法，经验证效果令人满意。

计算机应用；Loop细分曲面；细分小波；曲面边界处理

Loop细分模式是一种基于三角网格模型的细分方法[1]。随后，Hoppe等人对Loop细分方法进一步拓展，拓展的Loop算法具有任意性、整体连续性、算法稳定性和可伸缩性等，因此受到越来越多的关注。

近年来，小波技术在曲面造型中的应用也越来越广泛，对小波的多分辨率和“数学显微镜”等特性的应用，能够实现物体的快速造型和灵活修改[2-4]。随着对Loop细分曲面的研究进一步加深，Bertram于2000年给出了基于提升格式构造双正交 Loop细分小波的算法[5]，这在很大程度上提升了Loop细分曲面的形状可调节性。但是，到目前为止，笔者所看到的关于Loop细分小波的文献都只提到了对于网格内部顶点的小波分解和小波重构方法[5-6]，尚未见到针对非闭合曲面边界的小波分解和重构方法，而在工程应用中，非闭合曲面大量存在。针对有边界的非闭合网格，也有文章做了简单的处理，没有考虑内部点对边界的影响[7]。但对于类似面具（如图 1）这种非闭合网格，若仍然对其进行简单的边界处理而不考虑内部点对边界的影响，会造成小波分解结果的不合理性，所以对于边界如何进行有效的Loop细分小波处理显得尤为重要。

图1 非闭合曲面示例

1 双正交Loop细分小波介绍

1.1 Loop细分方法

细分曲面是多边形网格的极限状态，在曲面造型中应用很广。1987年Utah大学的Loop提出一种基于三角网格的细分模式[1]，所生成的曲面是箱样条(Box spline)曲面的推广。Loop模式采用1-4三角形分裂，只生成E-顶点和V-顶点（如图2所示）。

图2 1-4细分示意图

顶点计算规则如下：

即顶点本身与其所有相邻顶点的加权和，其自身的权值为nnβ-1，而邻点权值为

图3为Loop细分曲面实例。

图3 Loop细分曲面实例

1.2 基于提升格式的Loop双正交细分小波

细分曲面的小波分解过程可以看作将网格曲面上的细节特征分层去除的过程，而小波重构过程可以看作将细节特征添加到网格曲面的过程。Martin Bertram提出的Loop双正交小波是细分小波的典型范例[5]。

最简单的Loop细分曲面小波重构公式如下

e为小波顶点，v为尺度顶点，n为尺度顶点的邻点个数。

相对应的Loop细分曲面小波分解过程为其重构过程的逆过程。但如文献[5]中所述此种细分小波变换不能产生令人满意的效果，Bertram称其为“懒小波变换”(Lazy wavelet synthesis)，同时Bertram在文献[5]中给出了正交化的小波分解和重构方法。

提升格式是快速构造双正交小波的有效工具[8]。基于提升格式的正交化 Loop细分小波分解公式如下

提升格式的正交化Loop细分小波重构公式如下

其中，n为顶点v的邻点个数；iω为细分正交化系数，其计算过程和常用正交化系数参见文献[5]，在此不再赘述。图4为Loop细分小波分解实例。

图4 对重构网格执行loop细分小波分解的过程

2 边界处理

2.1 边界处理方法介绍

Bertram 提出的 Loop细分小波的构造中，只给出了对网格内部点的处理方法，而对非闭合网格的边界没有给出相应的处理。秦开怀等介绍过一种边界处理方式[8]，但此方法将边界当成分离曲线来处理，未充分考虑到内部点对边界的影响。

本文提出了另一种边界处理方法，避免了以上的不足。

对于具有边界的网格，先将其进行一次“虚复制”处理。所谓虚复制，即对非边界上所有的顶点和边，执行一次全局复制，这里的“复制”并非真正意义上的复制，而是仅存于大脑中。这样一来，结果相当于把内部所有的点和边看成是两份的重叠，边界点和边保持不变，如图5所示。因此，就可以得到以原网格边界为分隔线的封闭网格。换句话说，这一操作的目的就是把原网格的边界“造”成内部点和边，生成一张“半虚半实封闭网格”，而又不失其合理性。因为整个过程并没有改变原网格实际的几何信息和拓扑信息。该方法的最大优点是具备通用性，可以对具有任意边界的网格曲面进行细分小波处理。

图5 虚复制思想示意图，粗实线L为边界

2.2 具体实现及公式推导

与第1节提升格式小波分解过程相同，本文所述方法亦可分为4个步骤，下面分别阐述在小波分解的4个步骤中对边界点的处理与Bertram方法中对内部点处理的不同之处。

2.2.1 小波分解第一步

公式(5)等价于

其中，n为顶点v的邻点个数。当处理边界上的尺度顶点p时，如图5所示，首先计算p点的δ值时应改为公式

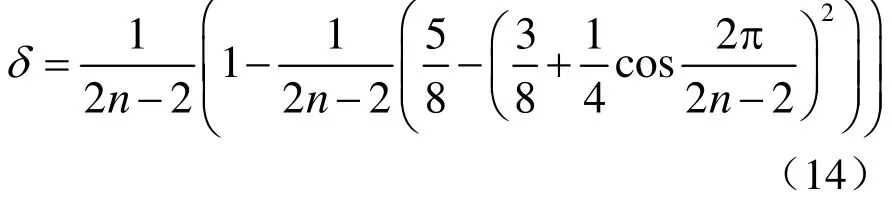
设与点p相邻的两个边界小波点分别为0e和1e，则处理边界时，式(13)更改为

2.2.2 小波分解第二步

第二步处理时，边界尺度顶点和内部尺度顶点的处理公式相同，只需把计算的公式更其中n为顶点p的邻点个数。

2.2.3 小波分解第三步

如公式（7）所示，细分曲面小波分解第三步以小波点为处理对象，要用到与该小波顶点有关的4个相邻尺度顶点信息。设与该边界小波顶点相邻的3个尺度顶点为0v,1v和2v，设其中2v为内部尺度顶点（如图6），则处理边界小波顶点时公式（7）要更改为改为

图6 小波顶点的分类

2.2.4 小波分解第四步

第一类：边界上的小波顶点；

第二类：有一个直接相邻尺度顶点和一个间接相邻尺度顶点为边界点的小波顶点；

第三类：只有一个间接相邻尺度顶点为边界点的小波顶点；

第四类：只有一个直接相邻尺度顶点为边界点的小波顶点。

因此，当执行第四步小波分解时，计算ω值之前先判断小波顶点e属于哪个类型，对于包含有边界尺度顶点的小波顶点e，计算ω值时，传入的各顶点的邻点个数可相应分为四种情况（与图6对应）。

（1） 对第一类：由虚复制原理可知，2v利用了两次。则计算ω时针对10,vv ,2v,2v传入的度分别为：220-n ， 221-n ，2n，2n；

（2） 对第二类：计算ω时针对10,vv ,2v,3v传入的度分别为：220-n ，1n，2n， 223-n ；

（3） 对第三类：计算ω时针对10,vv ,2v,3v传入的度分别为：0n，1n， 222-n ，3n；

（4） 对第四类：计算ω时针对10,vv ,2v,3v传入的度分别为：0n， 221-n ，2n，3n。

小波重构为小波分解的逆过程，在此就不再详述。

2.3 实 例

图7为对具有边界的网格模型执行小波分解的实例。

3 结 论

本文提出了一种非闭合Loop细分曲面小波变换的方法。该方法将网格的边界点“虚拟”成内部点，使对边界点和内部点的细分小波处理得到统一，并且得到了满意的结果。该方法具有通用性，可以用于具有任意边界网格的细分小波变换。

对于实际工程应用中的一些特殊需要，如将网格曲面用于数控加工中要求边界保持，即在小波分解过程中某些边界要求保持不变，在本算法中并未予以考虑。此问题将会在今后的工作中解决。

图7 对具有边界网格曲面执行Loop细分小波分解的实例

[1]Loop C T. Smooth subdivision surfaces based on triangles [D]. M.S. Thesis, Department of Mathematics, University of Utah, 1987.

[2]Daubechies I. Ten lectures on wavelets [M]. Phiadephia：SIMA Publ, 1992. 1-341.

[3]Biermann H, Martin I, Zorin D. Cut and past editing of multiresolution surfaces [J]. ACM Transactions on Graphics, 2002, 21(3)：330-338.

[4]Khodakovsky A, Schrode P, Sweldens W. Progressive geometry com- pression [C]// Proceedings of ACM Siggraph, 2000：271-278.

[5]Bertram M. Biorthogonal loop subdi-vision wavelets [J].Computing Springer, 2004, 72(1-2)：29-39.

[6]Lounsbery J M. Multiresolution analysis for surfaces of arbitrary topological type[D]. Ph.D.Thesis, Department of Mathematics, University of Washingtown, 1994.

[7]Wang H W, Qin K H, Tang K. Efficient wavelet construction with Catmull-Clark subdivision [J]. The Visual Computer, 2006, 22(9-11)：874-884.

[8]Sweldens W. The lifting scheme：A custom-design construction of bi-orthogonal wavelets [J]. Appl Comput Harmon Anal, 1996, 3(2)：186-200.

An Algorithm to Deal with Boundary of Meshes with Loop Subdivision Wavelets

ZHAO Gang, JI Bao-peng, BAI Jie
( School of Mechanical Engineering and Automation, Beijing University of Aeronautics and Astronautics, Beijing 100191, China )

Subdivision wavelets have been developed very fast in recent years. They are widely used in computer graphics, progressive transmission and multiresolution editing etc. Based on the lifting scheme, Bertram has introduced a bi-orthogonal wavelet construction for the Loop subdivision. The vertexes involved in the Bertram’s method are all inner ones in the subdivision surface. The paper presents a method to deal with the boundary of the mesh with subdivision wavelets. Tests show the feasibility of the approach.

computer application; loop subdivision surface; subdivision wavelets; surface boundary subdivision

TP 391

A

1003-0158(2010)06-0034-05

2009-03-18

国家自然科学基金资助项目（60603089）；北京市科技新星计划资助项目（2007B018）

赵 罡（1972-），男，河北文安人，副教授，主要研究方向为CAD/CAM，几何造型，虚拟现实。