纤维正则映射的无点刻画

周晓阳，冯丽

（1.大连民族学院理学院，辽宁大连 116605;2.大连电子学校，辽宁大连 116023）

纤维正则映射的无点刻画

周晓阳1，冯丽2

（1.大连民族学院理学院，辽宁大连 116605;2.大连电子学校，辽宁大连 116023）

纤维拓扑在近代拓扑理论中是发展较为迅速的一个分支，近些年来，许多数学家对此门学科给予了极大的关注和兴趣。与此同时，在计算机理论中，关于DCPO（有向完全偏序）的理论研究也一度成为该研究领域的一个热点，而Frame理论为其提供了有意义的推理和语汇。给出了纤维拓扑性质中的纤维正则映射的等价刻画，并利用Frame理论给出了纤维正则映射的无点刻画，从而使得Frame理论中关于纤维观点的运用更为方便、快捷。

Frame;纤维正则映射;拓扑

纤维拓扑的历史可追溯到一个多世纪之前Riemann的思想。纤维映射空间，作为纤维拓扑乘积的不交并，也出现在范畴拓扑的工作中。1989年，I.M.James出版了一本系统论述纤维拓扑的著作［1］，此著作通过研究纤维的拓扑结构与基空间的拓扑结构的内在联系，较系统地给出一般拓扑学中许多重要概念和命题在纤维拓扑理论中的刻画，促进了纤维观点在拓扑学中的发展，使纤维拓扑独立地成为一门学科。

近些年来，在计算机理论科学中关于DCPO的理论研究也一度成为热点，而Frame理论既是其中的一部分，也为其提供了有意义的推理和语汇。尽管关于Frame理论的文献很多，其研究也相当深入，但Frame理论的语汇却没有在纤维拓扑理论中运用。例如:如何用无点拓扑理论，即用Frame理论语言来刻画纤维拓扑中的主要概念。

本文将根据日本的Takuo Miwa［2］文章中的语言形式和I.M.James对纤维正则映射的定义将它们进行“保守推广”。

1 预备知识

由于在各种相关文献中，有些概念和符号的用法不完全一致，所以本节对文中使用的概念和表示符号予以必要的解释和说明。

设L是一完备格，满足第一无穷分配律，若只考虑L中的有限交以及任意并运算，称L是一个Frame或Locale。在两个Frame之间的映射f⊂A ×B，若该映射保有限交与任意并，称f为A到B的一个Frame态射或B到A的一个Locale态射。换句话说，若以Frame为对象，以Frame态射为态射的范畴称为Frame范畴，则其对偶范畴是Locale范畴。

对任意一个集合Y，Y上的纤维集X指的是（X，f），f是X到Y的映射，任意y∈Y，称f－1（y）为y上的纤维，它是X的子集，记Xy=f－1（y）。由于没有要求f是满的，因此y上的纤维可以是空集。对任意Y的子集Y'，称f－1［Y'］为Y'上的纤维集，记XY'=f－1［Y'］。当映射f:X→Y是连续映射时，称X是Y上的纤维拓扑空间，f是纤维映射，显然，Y的任意开集的逆像包含X中的某个开集。

对任意给定的拓扑空间Y，记FTY为纤维拓扑空间范畴，范畴FTY中的对象是到Y的连续映射，对范畴FTY中的任意两个对象f:X→Y，g:Z→Y，从f到g的态射是连续映射λ:X→Z，且满足f =g◦λ，把这个态射记作λ:f→g。态射λ:f→g是满的、闭的等等，即指λ:X→Z是满的、闭的等等。

对任意给定的Frame A，记FFA为纤维Frame偶范畴，范畴FFA中的对象是定义域为A的Frame态射，对范畴FFA中的任意两个对象f:A→B，g:A→C，从f到g的态射是Frame态射λ:B→C，且满足g=λ◦f，把这个态射记作λ:f→g。态射λ:f→g是满的、闭的等等，即指λ:B→C是满的、闭的等等。

若X是一拓扑空间，以Ω（X）表示其拓扑，易知按集合的交、并运算，Ω（X）构成一个Frame或Locale，我们称其为空间X的开集Frame或开集Locale。若f:X→Y是一连续映射，Ω（f）:Ω（Y）→Ω（X）定义为

这里特别提到一个表示约定:当f⊂A×B是一个A到B的映射时，f（x）与f［x］的区别在于f （*）中只代入A中的元素，而f［*］中只能代入A的子集。

对于一个FrameA，通常ptA表示的集合可以有三种理解:

（1）A中的所有完全素滤子;

（2）A到2={0，1}的所有Frame态射;

（3）A中的所有素元。

在无特别说明时，我们采取（3）的用法，即ptA表示A中的所有素元。

下面的记法在本文中也是特别的:

记Ω（ptA）=φ［A］，Ω（ptA）实际上已经构成ptA上的一个拓扑，在无任何附加说明时，ptA永远表示以Ω（ptA）为拓扑的拓扑空间。若φ是单射，称A为空间式Frame。

记A，B是空间式Frame，g:A→B是Frame态射，

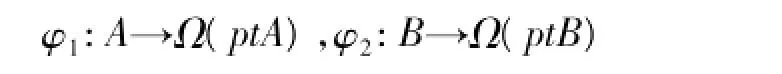
都是同构映射，记f=ptg:ptB→ptA是拓扑空间之间的连续映射，且满足f－1=φ2gφ－11，称映射f是由Frame态射g诱导的映射。

当拓扑空间X给定时，x∈X，Nx表示x的所有邻域组成的集合。表示A在X中的闭包，IntA表示A的内部，在基本集明确的条件下，Ac总表示A的余集。

其他没有特别提及的概念及相关结果，拓扑学参见文献［3－4］，Frame理论参见文献［5］，范畴论可参见文献［6］。

2 纤维正则映射的无点刻画

为了讨论纤维正则映射的无点刻画，首先，说明纤维正则映射的相关概念。

定义1.1［2］设f:X→Y是连续映射，X，Y是拓扑空间，如果对任意x∈X，任意闭集F⊆X，x∉F，存在U∈Nf（x），使{x}∩f－1［U］与F∩f－1［U］在f－1［U］中有不交邻域，则称f:X→Y是纤维正则映射。

定义1.2［1］设f:X→Y是连续映射，X，Y是拓扑空间，对任意x∈f－1（y），y∈Y，任意N∈Nx，存在W∈Ny和［W］⊆N，则称f:X→Y是纤维正则映射。

定义1.1和定义1.2分别出现在两个不同的文献中，虽然表达方式不同，但经过以下简单的证明，得知它们是等价的。

证明已知定义1.1，对任意x∈f－1（y），y∈Y，任意N∈Nx，XN是闭集，且x∉XN，则∃W∈Ny，使{x}∩f－1［W］与XN∩f－1［W］在f－1［W］中有不交邻域，即

推论1.1设A，B是空间式Frame，g:A→B是Frame态射，则g:A→B是纤维正则态射⇔由g诱导的映射f=ptg:ptB→ptA是纤维正则映射。

证明由定理1.1知:f:ptB→ptA是纤维正则映射，当且仅当，Ω（f）:Ω（ptA）→Ω（ptB）是纤维正则态射，而A，B是空间式Frame，则A与Ω（ptA）同构，B与Ω（ptB）同构，即A，B可分别看作pta，ptB上的拓扑，显然，推论成立。

推论1.1证明了Frame范畴中纤维正则映射的保守推广。

［1］JAMES Ioan Mackenzie.Fibrewise Topology［M］.Cambridge:University Press，1989.

［2］BUHAGIAR David，MIWA Takuo，Covering properties on maps［J］.Q＆A in General Topology，1998，16:53－66.

［3］ENGELKING Ryszard.General Topology［M］.Berlin: Heldermann Verlag，1989.

［4］儿玉之宏，永见启应.拓扑空间论［M］.方嘉林，译.北京:科学出版社，1984.

［5］郑崇友，樊磊，崔宏.Frame与连续格［M］.北京:首都师范大学出版社，2000.

［6］MAC LANE Saunders.Categories for the Working Mathematician（Graduate Texts in Math）［M］.New York: Springer－Verlag，1998.

Pointless Description of Fibrewise Regular Maps

ZHOU Xiao－yang1，FENG Li2
（1.School of Science，Dalian Nationalities University，Dalian Liaoning 116605，China;2.Dalian Electronic School，Dalian Liaoning 116023，China）

Fibrewise Topology is a branch of modern topology theory，which develops very quickly。Recently，many mathematicians have taken tremendous interest in this subject。Meanwhile，the theory about DCPO（Directed Complete Partial Order）in Theoretical Computer Science has been also a hot spot，and the theory of Frames supplies a lot of important reasoning.The equivalent characterization of fibrewise regular map in fibrewise topology has been presented，and by the theory of Frames，the pointless description of fibrewise regular maps has been also developed.Therefore，it will be convenient and fast to apply the fibrewise viewpoint in the theory of Frames.

frame;fibrewise regular maps;topology

O189.1

A

1009－315X（2011）03－0277－03

2011－03－24;最后

2011－04－01

周晓阳（1981－），女，辽宁大连人，讲师，博士，主要从事空间理论、算子理论和拓扑理论研究。

（责任编辑 邹永红）