9自由度混联微创外科机器人的正反解
张 帆 刘 达 王田苗
(北京航空航天大学 机械工程及自动化学院,北京 100191)
9自由度混联微创外科机器人的正反解
张 帆 刘 达 王田苗
(北京航空航天大学 机械工程及自动化学院,北京 100191)
针对北京航空航天大学机器人研究所最新开发的用于胸腹部冷冻穿刺手术的 9自由度“5R+4T”混联机器人,基于指数积公式,利用反变换法和逆矩阵的特性,提出了一种在单约束条件下,得到该机器人解析形式正反解的新算法.通过数值算例验证了正反解的互推性,即算法的有效性,并经过对算例的分析给出了修正方案,扩大了算法的适用范围.该方法克服了因为混联机器人自由度多、结构复杂而带来的难以完成正反解计算的困难,为多自由度混联机器人的运动学求解提供了一种新的思路.
微创外科;混联机器人;正反解;指数积
机器人的正解与反解计算作为一对互逆的过程是机器人运动学研究中最基本的问题.诸如工作空间的计算与描述、灵活性和刚度的评价以及机器人的实时控制和轨迹规划等研究工作都以其为基础.常见求解方法有很多,如经典的“D-H”法[1],基于指数积的子问题法[2]以及其他基于旋量的方法等.然而,使用上述方法的研究基本都以常规的串联机器人或并联机器人为对象[3-5],对于多自由度混联机器人的整体运动学建模的相关研究报道甚少.
本文所做的工作是针对北京航空航天大学机器人研究所最新开发的用于胸腹外科冷冻穿刺手术的“5R+4T”(R指旋转关节,T指移动关节)9自由度混联机器人进行的.传统的分析方法如“D-H”法,因为初始坐标系设置的复杂性,以及由此带来的计算可行性的下降使其并不适用于混联机器人的运动学求解.文献[6]对该机器人做过运动学的分析,但其方法对机器人拓扑结构有较大的简化,而且只得到了数值解.本文基于指数积公式,利用反变换法和逆矩阵的特性,得出了单约束条件下此种 9自由度混联机器人的解析形式正反解,即封闭解,并通过正反解的互推,验证了其正确性.研究结果为将来的全主动关节形式下,机器人的位置控制提供了必要的理论前提和基础.
1 机器人本体介绍
如图 1所示,混联机器人由一个“5R”的串联机械臂和其末端夹持的一个“4T”的并联平台组成.

图 1 混联微创外科穿刺机器人
其主要功能是在 CT(Computed Tomography)图像的导引下,根据医生的要求,实现穿刺针的空间定位.串联臂的各个关节可通过一个踏板控制,经由其内部液压力来锁紧或松开,其功能是在较大的范围内进行粗定位.并联平台由结构完全一样的上下两层组成,每一层都类似于一个 x-y工作平台,具有两个方向相互垂直的移动自由度,能够分别使其上的球铰在该层所在平面内运动,从而实现小范围内的精确定位.上下两个球铰的中心可以确定一个空间矢量,即:穿刺针的进针矢量.医生在由两个球铰组成的滑道的导引下,沿着进针矢量将穿刺针推入病人体内,完成穿刺过程.
2 运动学正解
对于“5R+4T”的混联机构,运动学正解是指:在已知全部 9个关节的关节变量的情况下,求出穿刺针针尖点的位置坐标.为解决这一问题,可将串联部分与并联平台的上下两层分别组合,组成两个形式相同的“5R+2T”串联分支,分别称为上分支和下分支,如图 2所示.

图 2 混联机器人结构
2个分支的前 5个关节(即串联臂)是共用的,拥有相同的关节变量.通过各自所拥有的 7个运动副,两个分支分别能确定一个球铰点的空间位置.同时,设定穿刺针沿两个球铰所定的方向进针并完成穿刺后,其尾端与上分支的球铰中心重合,而针尖与目标点重合,即:在机器人的最终位形下,上球铰中心与目标点之间的距离等于穿刺针的长度.至此,整个混联机构的正向运动学解算就集中转化为求解上、下分支的运动学正解.
而指数积公式在求解串联结构的正向运动学时具有很大的便利性.通过对每个关节轴定义一个单位运动旋量 ξ,可以在只设定基坐标系和末端的工具坐标系两个坐标系的前提下,利用所有关节单位运动旋量的连乘积表示出上述两个坐标系的相对位置关系,从而求得正解[7].
取图 2中所示位形为初始位形,建立基坐标系和工具坐标系.上述两图中的工具坐标系实际分别都建立在上下分支的球铰中心处,但因为不考虑移动副的机械结构限制,认为初始时球铰中心能经由两个移动关节收回到并联平台的角点处,故工具坐标系位于图 2中所示的 C点和D点.
初始位形时,上下两个分支的工具坐标系相对于基坐标系的变换矩阵分别为
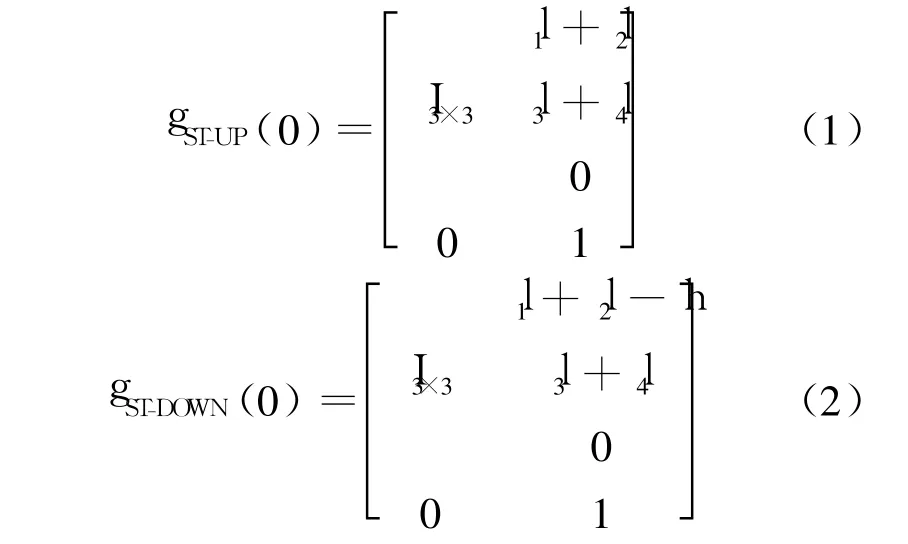
式中,I3×3表示 3阶的单位矩阵;l1,l2,l3,l4和 h均为结构参数.
图 2中 9个关节的单位运动旋量 ξ1~ξ7,ξ66和 ξ77计算如下:


考虑到

则

根据指数积公式,上分支的工具坐标系相对于基坐标系的变换矩阵可以表示为

该矩阵第 4列的前 3行即为上分支球铰中心点 S1的坐标(x1,y1,z1)T.
同理,下分支的工具坐标系相对于基坐标系的变换矩阵为

该矩阵第 4列的前 3行即为下分支球铰中心点 S2的坐标(x2,y2,z2)T.
此时,穿刺针的方向矢量即为

令(cosα,cosβ,cosγ)为穿刺针矢量的方向余弦,则

令 L为穿刺针的长度,即平台上平面球铰中心点S1到穿刺针针尖点 E的距离,则E点的坐标为

通过以上正解的过程,可以看出,在对混联机器人拓扑结构进行合理的分拆后,其正解的特点类似于传统串联机器人的正解,相对比较简单,也能充分发挥出指数积公式初始坐标系设置简单的优越性.
3 单约束条件下的反解
反解的过程是首先经由穿刺针末端点的坐标和针的长度及姿态矢量回推出上平台球铰中心点S1的坐标,再根据手术需要给出并联平台上的工具坐标系的姿态矩阵 R(θ).以这两个条件作为反解初始条件,首先对上分支 7自由度串联结构进行附加约束条件的解算,得到 θ1~θ7的值.再根据已求出的 θ1~θ5,利用逆矩阵的特性,解出下分支中的 θ66和 θ77,从而完成全部 9个关节的反解.
3.1 反解初始条件
已知穿刺针末端点 E(xE,yE,zE),穿刺针长度 L,穿刺针姿态(α,β,γ),以及 3阶的并联平台姿态矩阵 R(θ),则平台上平面球铰中心点 S1的坐标即为

根据由点 S1的坐标和 R(θ)构成的gST-UP(θ)可以对由 7个运动副串联而成的上分支进行运动学反解,进而得到 7个关节变量 θ1~θ7的值.
3.2 上分支反解
根据实际操作经验,串联臂的第 4关节在实际手术中很少需要做大幅度转动,经常处于相对固定的位置.因此,本文将 θ4角固定,这样的简化使得在实际手术需要仍能得到满足的前提下,算法的可解性大为改观.此即为约束条件.

式(14)两端的元素(3,1)对应相等,可以得到以下的关系式:



式中,±号对应于 θ1的两个可能解.选定 θ1的解之后,再令式(14)两端的元素(1,1)和(2,1)分别对应相等,可得只要 c4≠0,便可求出


当 c4=0时,操作臂处于奇异形位.此时,关节轴 2,3和 5平行,只能解出 θ2+θ3与 θ5的差.奇异位形可由式(18)中 arctan2的两个变量是否都接近 0来判断.若都接近 0,则为奇异形位,否则不是奇异形位.在奇异形位时,可任意选取θ2+θ3的值,再计算相应的 θ5值.

式(19)两边元素(2,2)和(3,2)分别对应相等,得
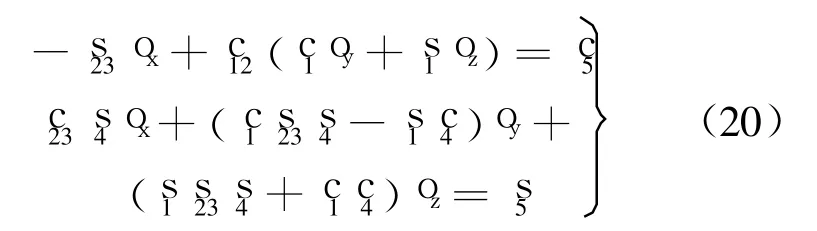
由此得到 θ5的解:

再令式(14)两边元素(1,4),(2,4)和(3,4)分别对应相等,可得如下方程组:

对式(22)中的已知量进行移项合并,并做代换处理,可得

通过式(23)中 3个方程彼此间的线性运算,可以将 θ6和 θ7消去.再对已知量做代换处理,进而能够得到:

式中,A1~A9,B1~B3均为由已知量组成的代数式.
观察式(24)的形式,与式(15)相同.所以可以采用求解 θ1的方法来求解 θ2.同样,θ2有两个解 ,在选定 θ2的值后,根据式 (18),θ3的解即为


上述矩阵方程两边元素(2,4)和(3,4)分别对应相等,可得 θ6和 θ7.因其结果一目了然,在此不再赘述.
3.3 下分支反解
如图 3,只考虑包括前 5个旋转关节在内的串联部分,设置末端坐标系 T和基坐标系.初始位形时,末端坐标系相对于基座标系的变换矩阵为

因此,根据指数积公式,末端坐标系相对于基坐标系的变换矩阵为

又因为,对于

有

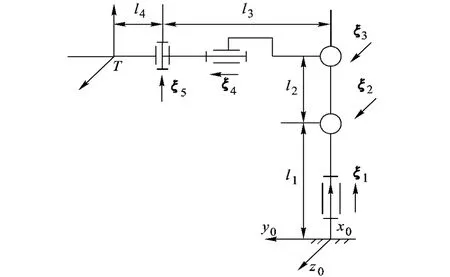
图 3 串联机械臂结构
根据式(30),可以求出基坐标系相对于末端坐标系的变换矩阵 g-1ST(θ),进而可以将已知的 E点和 S1点在基坐标系下的坐标表示变换为在末端坐标系 T下的表示,即

式中,E,TE,S1和TS1均为齐次坐标表示.
在末端坐标系 T下,令

则穿刺针所在直线的方程为

又,并联平台下层所在的平面可表示为

将式(33)和式(34)联立,可解出下分支球铰中心点 S2的坐标 (在末端坐标系 T下的表示),即

从而,可得到下分支两个移动副的关节变量的值,即

至此,θ1~ θ7,θ66,θ77全部 9个关节变量均得解,运动学反解完成.
由式(16)可知,在分别取正号或负号时,θ1有两组解,而 θ2亦如此.根据排列组合原理,在本文提出的算法下,任一个可达的末端位姿经由反解,将对应 4组可能的关节变量值.若不考虑各关节机械结构的限制,仅从数学角度来看,这 4组解都应该是正确的.
4 数值验证
针对以上所述的正反向运动学的求解,通过Matlab编程,进行了验证.具体采用的是一种虽然传统但却十分有效的方法,即:先为各个运动关节任取相应的关节变量值,进行正向求解;再利用正解的结果,代入反解的算法中,求出各个关节变量;然后对一开始任取的各关节变量和经过反解求出的各关节变量进行比较,如果二者相同,则可说明算法本身的自洽性和有效性.
考虑各个关节的最大行程,任意给定 9个关节变量的值,如表 1中的第Ⅰ组数据所示.经过先正解再反解的运算,得到包括其本身在内的 4组反解值,见表 1.
由表 1中的运算结果可以看出,只有当 θ1和θ2的求解公式都取正号时,正反解的互推关系才能成立.
表 2中,任选了 5组关节变量值,对混联机器人正反解算法的互推性进行验证.经过运算,1~3组可以很顺利地完成互推,而第 4组和第 5组则代表不同于前 3组的比较特殊的一类.这两组值在选定 θ1和 θ2求解公式的正负号后,经解算得出的 9个值中,会出现 θ2的异常突变,表现为绝对值过大,以至于接近 2π,并间接导致 θ3计算结果的错误.但与此同时,θ2+θ3和其余 7个关节变量的结果却都是正确的.这主要是由 θ2求解公式本身的复杂性,及三角函数以 2π为周期的特性共同作用而导致的.对于第 4组数据,会得到一个绝对值较大的负值;而第 5组数据,则会得到一个绝对值较大的正值.要想解决这个问题,只需要给这两个异常的 θ2分别加上和减去一个 2π便可以得到正确结果.因此,在实际运算时,就需要对本文提出的算法设置一个修正环节.当经过原算法计算后,若发现 θ2的值异常偏大,就减去一个2π;反之,则加上一个 2π.

表 1 4组反解值

表 2 5组验证用数据
5 结 论
综上所述,本文基于指数积公式,利用反变换法和逆矩阵的特性,建立了本文中所研究的 9自由度混联机器人的正反解算法,得到了单约束条件下的封闭解.该过程具有类似于求解串联机器人运动学的特点,即:反解较难,正解相对简单.通过数值算例,证明了算法的有效性,并提出了修正方案.
References)
[1]熊有伦,唐立新,丁汉,等.机器人技术基础[M].武汉:华中科技大学出版社,1996 Xiong Youlun,Tang Lixin,Ding Han,et al.Fundamentals of robotics[M].Wuhan:Huazhong University of Science and Technology Press,1996(in Chinese)
[2]理查德·摩雷,李泽湘,夏恩卡·萨思特里.机器人操作的数学导论[M].北京:机械工业出版社,1998 Murray R M,Li Zexiang,Sastry S S.Amathematical introduction to robotic manipulation[M].Beijing:China Machine Press,1998(in Chinese)
[3]Jin Yan,Chen I-Ming,Yang Guilin.Kinematics analysis of a 6-DOF selectively actuated parallel manipulator[C]//Proceedings of the 2004 IEEE Conference on Robotics,Automation and Mechatronics.Singapore:IEEE,2004,1:231-236
[4]赵杰,刘玉斌,蔡鹤皋.一种运动旋量逆解子问题的求解及其应用[J].机器人,2005,27(2):163-167 Zhao Jie,Liu Yubin,Cai Hegao.Solution for one type of inverse kinematics sub-problem in screw theory and its application[J].Robot,2005,27(2):163-167(in Chinese)
[5]钱东海,王新峰,赵伟,等.基于旋量理论和 Paden-Kahan子问题的 6自由度机器人逆解算法[J].机械工程学报,2009,45(9):72-76 Qian Donghai,Wang Xinfeng,Zhao Wei,et al.An algorithm for the inverse kinematics calculation of 6-DOF robots based on screw theory and Paden-Kahan sub-problems[J].Journal of Mechanical Engineering,2009,45(9):72-76(in Chinese)
[6]Tang Can,Liu Da,Wang Tianmiao,et al.The kinematics modeling based on spinor theory for CT-guided hybrid robot[J].High Technology Letters,2009,15(1):20-25
[7]Brockett RW.Robotic manipulators and the product of exponentials formula[C]//Fuhrman P A.Mathematical Theory of Networks and Systems.Berlin:Springer-Verlag,1984:120-129
(编 辑:赵海容)
Forward and inverse solution of a 9-DOF hybrid robot for minimally invasive surgery
Zhang Fan Liu Da Wang Tianmiao
(School of Mechanical Engineering and Automation,Beijing University of Aeronautics and Astronautics,Beijing 100191,China)
Focusing on the recently developed“5R+4T” 9-DOF(degree-of-freedom)hybrid robot for thoracoabdominal percutaneous cryosurgery by the robotics institute of Beijing University of Aeronautics and Astronautics,an original single-constraint-condition algorithm was put forward to obtain analytic solutions to the forward and inverse kinematics of the robot,based on the productof exponentials(POE)formula using inverse transformationmethod and characteristics of inversematrix.Themutual derivation between the forward and the inverse solution,namely,the effectiveness of the algorithm,was demonstrated by several sets of numeric data.Amodification for the algorithm was also advanced by discussing the demonstration results,so as to expand the range of its applicability.This algorithm overcomes the difficulties in performing the forward and inverse kinematic calculations which result from the DOF redundancy and the structure complexity of the hybrid robot,bringing a new idea about solving kinematic problems of multi-DOF hybrid robots.
minimally invasive surgery;hybrid robot;forward and inverse solutions;product of exponentials(POE)
TP 242
A
1001-5965(2011)04-0446-06
2010-01-26
科技部国际合作资助项目(2006DFA 12290)
张 帆(1983-),男,河北石家庄人,硕士生,kurtgre@gmail.com.

