卫星定位和精度因子的改进方法

陈灿辉 张晓林

(北京航空航天大学 电子信息工程学院,北京 100191)

卫星定位和精度因子的改进方法

陈灿辉 张晓林

(北京航空航天大学 电子信息工程学院,北京 100191)

在卫星导航定位系统中,在精度因子计算和采用最小二乘法进行定位求解时,传统上采用测量矩阵直接求逆方法来进行.为了克服矩阵求逆带来的计算量大和数值稳定性差的不足,利用测量矩阵的对称正定性,提出了一种基于矩阵 UTDU分解的定位解算和精度因子计算方法.改进方法具有严格的数学理论基础,保证了方法的正确性和有效性.数值分析结果表明,相对直接求逆的传统方法而言,在定位解算时,该方法能降低约 60%的运算量,而在精度因子计算中,约能降低 36%的运算量.且改进方法能大大降低求解矩阵的条件数,提高了求解的数值稳定性.

卫星导航;最小二乘;解算;精度因子;矩阵分解

全球导航卫星系统(GNSS,Global Navigation Satellite System)是一种以空间卫星为基础的无线电导航与定位系统,该系统能为全世界任何地方的用户全天候、全时间、连续和实时地提供三维位置、速度和时间 (PVT,Position,Velocity and Time)信息.由卫星导航定位系统确定的位置和时间的精度取决于各种因素错综复杂的相互作用.粗略来讲,基于伪距的定位精度可以表示为精度因子(DOP,Dilution of Precision)和伪距误差的乘积[1-3].为了提高定位精度,必须选择精度因子小的卫星星座进行定位,计算精度因子是定位解算中必不可少的过程.另外,在采用 GNSS进行导航定位时,由于可见卫星数很多,在接收机容量和运算速度等因素的限制下,一般情形是不可能采用所有可见卫星来进行定位的,这时,就要进行选星,以选择星座可用性满足设计要求或是星座几何精度因子(GDOP,Geometric Dilution of Precision)最优的少数可见星来进行定位,这也就需要进行精度因子求解.传统上,计算精度因子采用矩阵求逆方法,计算量大,特别是在多星座组合导航中动态条件下需要频繁进行选星操作时,其计算量更是一个极为突出的问题.此外,在各种伪距定位算法中,最小二乘法是一种比较简单、基本而又有着广泛应用的重要方法[3],该方法依据线性化定位模型进行迭代求解.由于最小二乘法每步迭代都涉及矩阵的乘法和求逆运算,因而整个迭代过程要多次重复这一过程,这无疑会增大导航解算的计算量与存储量,从而影响实时定位的精度.因而,为了保证实时处理的要求,对接收机处理器速度的要求就大大提高了,这也就大大加重了用户接收机的负担,使其成本上升.

为了解决上述问题,探索新的、适合于卫星导航定位系统的快速获取定位信息和精度因子的方法就显得迫切而重要,并具有极为重要的现实意义和应用价值.

为了实现导航方程的快速求解,人们提出了一系列方法[4-6].文献[4]提出了一种定位求解的递推方法,但它是针对单星座系统来进行算法设计的,对多星座组合系统而言,随着可见卫星数的大幅增加其计算量也会增加;文献[5-6]提出了导航方程的非迭代解法,但它们均是针对单卫星导航系统来进行算法设计的,在多星座组合系统中难以直接采用.在 GNSS中,多星座组合导航势成必然,针对 GNSS中快速导航定位的需要,并考虑到在导航定位系统中最小二乘法应用的广泛性,这里从传统的最小二乘法出发,针对其不足,提出了新的基于实对称矩阵 UTDU分解的改进算法.该算法一方面避免了由于矩阵求逆带来的计算量大而使得定位解算实时性降低的问题,可实现 GDOP值和定位求解的快速计算,降低计算复杂度;另一方面,分解方法能有效降低求解矩阵的条件数,改善计算过程的数值稳定性.

1 定位求解与精度因子计算

在卫星导航定位系统中,基于伪距定位的测量方程如下[1-3]:

其中,y表示伪距预测值与测量值之差,y∈Rn,n表示可见卫星数;x表示状态变量的增量,x∈Rm,m表示状态量维数,有 m=3+nsys,nsys表示卫星系统个数,状态变量的前三个元素是接收机三维位置坐标,其它元素表示接收机钟差;ε是测量误差矢量;H是 x和 y之间的线性关联矩阵,也称为方向余弦矩阵,H∈Rn×m.例如,对于双星座组合导航定位系统,H具有如下形式:

其中,axj,ayj,azj表示第 j颗卫星的方向余弦.

采用最小二乘法进行定位求解时,可得 x与y的关系:

称 M=HTH为测量矩阵,M∈Rm×m.

几何精度因子 GDOP的表达式为

其中,VGDOP为 GDOP之值;tr(·)为求矩阵之迹.

由式(3)、式(4)可见,不管是进行定位求解还是进行精度因子的计算,如果采用常规方法,则对测量矩阵 M进行求逆运算是不可避免的.由于进行定位求解时需要进行迭代运算,且在选星过程中,也要对多种卫星组合方案的 GDOP值进行求解运算,其计算量很大.特别是在多星座组合导航定位系统中,因为测量矩阵 M的阶数会随着星座个数的增加而增加,而矩阵求逆中乘法和加法的运算量约与其阶数的三次方成正比,因此在采用常规方法进行计算时,其计算负荷更显突出,也会占用较多的时间,这对动态用户特别是高动态用户接收机而言是一个非常严峻的挑战.另外,从式(4)还可以看出,如果只是进行精度因子的计算,并不需要知道测量矩阵的逆矩阵中的全部元素,只需求出其主对角线元素即可,这就促使人们采取一些改进算法来达到该目的,以获得运算量的降低.文献[7]提出了一种计算 GDOP的闭合公式,但该方法只适合单星座 4星状态下的求解计算.文献[8]以矩阵特征值与特征多项式的关系为基础提出了一种可有效降低 GDOP求解运算量的方法,但它是针对单星座系统进行的,并且需要计算矩阵 M的行列式.文献[9]以方向余弦矩阵 H的 QR分解为依据提出了一种计算 GDOP的改进算法,可知,QR分解的计算量很大,使用Gram-Schmidt方法对一个 n阶方阵进行 QR分解大概需要 n3次乘法(是 LU分解的 3倍),并有大约相同次数的加法[8].而对一个 n×m维矩阵进行 QR分解,在卫星系统数确定、即 m一定的情形下,其乘法和加法运算次数均与 n2成正比,从而,当可见卫星数较多,即 n较大时,该方法的运算量也比较大.另外,在卫星导航定位系统中采用最小二乘法进行用户速度测量时,也采用与式(3)同样的方式进行求解,即速度与位置求解的测量矩阵是相同的.对于有相同系数矩阵的问题,LU分解是一种有效处理方法[10].因此,综合考虑以上因素,本文以 LU分解为基础,提出了一种进行定位求解和精度因子计算的改进方法.同时,考虑到测量矩阵 M的对称性,这里实际采用的是基于对称矩阵的 LU分解,即 UTDU分解.

2 卫星定位与 DOP的改进方法

在卫星导航定位系统的实际使用中,一般来说,测量矩阵 M是对称正定矩阵[3],由线性代数理论可知,它可进行 UTDU分解,且分解是唯一的[9],即有

其中,U为单位上三角矩阵;D为对角矩阵;它们的阶数与矩阵 M相同,即 U,D∈ Rm×m.矩阵 U,D形式如下:

设矩阵 M中的元素为 mij(i,j=1,2,…,m),通过推导,可得其 UTDU分解算法:

从而,定位求解方程式(3)可变换为

其中,b=HTy.求出 b后,按回代求解方式[8]可获得 x的值,这样,即可避免迭代求解过程中的矩阵求逆运算.对于矩阵 UTDU分解的计算量,根据式(8),可推导出如下结论:

m阶实对称矩阵 UTDU分解算法中,乘法(含除法,下同)的运算次数为(m3/3+m2/2-5m/6),加法的运算次数为(m3-m)/6.

而 m阶方阵求逆算法中,其乘法和加法的运算次数均约为 m3.例如,对双星座组合导航系统而言,有 m=5,矩阵 M的 UTDU分解算法中乘法次数为 50,加法次数为 20,而求逆计算时,乘法和加法次数均约为 125次.显然,采用 UTDU分解方式可节省约 60%的乘法和 80%的加法运算,其计算量的改善值是很大的.而采用式(9)的回代求解方法中(不考虑 HTy的计算量),其乘法运算次数为 m2,加法运算次数为(m2-m),与采用求逆后再进行直接求解的方法相比,并不会增加计算量.由此可见,采用 UTDU分解方法进行求解可有效降低运算量.

根据分解结果可得

可以证明,单位上三角矩阵的逆仍为单位上三角矩阵,故可令

经推导,可得到计算 U-1中元素的算法,有

在该算法中,乘法和加法的运算次数均为(m3/6-m2/2+m/3).

由式(4)可知,计算 GDOP时只需要求出矩阵 M-1的主对角线元素,根据式(10),即可推导出求解精度因子的算法:

设矩阵 M-1的主对角线元素为 δi(i=1,2,…,m),则有

该计算式中,乘法运算次数为(m2-m),加法运算量为(m2-m)/2.根据式(4)即可得到GDOP的计算式,有

对于其它类型的精度因子,由 δi的值即可根据各精度因子的定义[1]进行计算,如:

其中,VHDOP为水平精度因子之值;VVDOP为垂向精度因子之值;VPDOP为位置精度因子之值;VTDOP为时间精度因子之值.由此可知,在进行精度因子计算时,只有 GDOP是与测量矩阵 M的逆的迹相对应,而对其它精度因子,只有得到矩阵 M-1的各主对角线元素之后才能进行计算.因此,在卫星导航系统中,也就难以采用通用的求矩阵之逆的迹的方法来进行各精度因子计算.

由上面的分析可知,基于 UTDU分解,通过式(12)、式(13)得到 m阶矩阵 M-1的主对角线元素的方法,其计算量为(m3+2m2-3m)/2次乘法,(m3-m)/3次加法.通过矩阵求逆方式获取m阶矩阵 M-1的主对角线元素约需要 m3的乘法和基本相同次数的加法运算,因此采用本文所述改进方法能有效降低精度因子的计算量,特别是在多星座组合导航定位系统中,矩阵 M的阶数 m是随着星座数的增加而增加的,从而其计算量的降低量将更为明显.例如,在双星座组合导航定位系统中,m=5,采用本文所述改进方法计算矩阵M-1的主对角线元素时,需要 80次乘法和 40次加法运算;而采用直接求逆方式时,则需要约 125次乘法和加法,以乘法来衡量,降低了约 36%的运算量.当然,采用直接求逆方式来进行精度因子求解,125次乘法运算量并不大,采用改进方法节省 45次乘法运算似乎意义也不大.的确,对于计算一次 DOP而言,其改进意义是不很明显,但在诸如选星求解等过程中,需要在一次求解中进行成百上千次 DOP计算的情形下,其计算量的改善意义就可得到充分体现.例如,如果在某次选星过程中需要进行 100次 DOP计算(事实上,这是很普遍的,通常的选星方法其 DOP计算次数会比这大得多),则改进方法可节省约 4 500次乘法运算和约 8500次加法运算,其改善值很大.

由以上分析过程可知,在采用 UTDU分解方式进行 PVT求解和精度因子计算时,求解过程中需要形成 3个矩阵 U,U-1和 D.在实际操作过程中,为了降低存储空间,事实上,并不需要定义 3个矩阵来存储它们,而只需定义一个矩阵即可,例如,就采用矩阵 U来存储这 3个矩阵,此时,矩阵U中的元素排列如下:

3 性能分析

基于 UTDU分解的方法具有严格的数学理论基础,因此,本文所提改进方法的正确性和有效性是毋庸置疑的.下面对该方法的复杂性等性能进行进一步分析讨论.

3.1 复杂性

由前述分析可知,对于基于 m阶矩阵的UTDU分解方法,只需按式(8)计算出矩阵 D的主对角元素和矩阵 U的主对角线以上元素,其求解运算量是 O(m3/3)阶的,而直接求逆方法的求解运算量是 O(m3)阶的,显然,改进方法求解更为简洁.图 1所示是在采用双系统定位时,在不同可见卫星数和不同迭代次数情形下,采用本文所述 UTDU分解法相对采用式(3)所示传统的直接求逆法相比其乘法运算量的改善百分比曲线.由图 1可见,新方法能节省 60%以上的运算量.

图 1 PVT求解中UTDU分解方法相对传统直接求逆法运算量改善百分比曲线

根据前述分析可知,在 DOP求解中,在双系统条件下,采用对测量矩阵 M进行直接求逆时约需 125次乘法运算,而采用 UTDU分解方法时只需约 80次乘法运算,可节省约 36%的运算量.文献[9]提出采用矩阵的 QR分解来计算 DOP的改进算法,本文对基于 UTDU分解方法与基于 QR分解方法的运算量进行了比较,图 2所示为UTDU分解法相对 QR分解法乘法运算量的改善百分比曲线.由图 2可见,UTDU分解法比 QR分解法的计算量小得多,且随着可见卫星数的增加,改善量会大幅增加,当可见卫星数在 13颗以上时,运算量的改善量超过 90%.

图 2 DOP求解中UTDU分解方法相对QR分解法运算量改善百分比曲线

3.2 矩阵条件数

矩阵条件数常常用来衡量矩阵的病态性.考虑到矩阵范数的等价性,为简单计,取矩阵范数‖·‖∞来进行条件数的计算,从而,对任意可逆矩阵 A,其条件数计算式可表示为

在卫星导航定位系统的实际使用中,有时会出现测量矩阵 M为病态的情形.采用 UTDU分解法进行求解时可避免对矩阵 M的直接运算.采用分解法按式(9)所示形式进行回代求解时,其回代过程分为 3步:

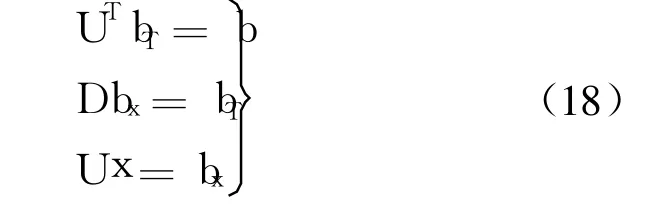
式中,bT,bx为中间变量;矩阵 D为对角阵.显然,第 2个回代求解方程 Dbx=bT其实就是简单的除法运算,从而,考虑分解矩阵的条件数时,只需考虑矩阵 U和 UT的条件数即可.显然,矩阵 U和UT的病态性是相同的,故只需计算矩阵 U的条件数.

下面,以具体实例来分析测量矩阵 M及UTDU分解后矩阵的条件数.

例如,在某双星座组合导航定位系统中,某时刻得到的测量矩阵为

经计算,可知其条件数为 fcond(M)=4.546 5×106.显然,此时矩阵 M的病态性较严重.而在采用本文所述分解法后,经计算,矩阵 U的条件数为 fcond(U)=202.75,相对原矩阵条件数而言,降低了 4个量级,矩阵 U已经是良态矩阵了.这就说明,通过分解方法能获得条件数小得多的求解矩阵,可有效改善求解矩阵的病态性,提高求解的数值稳定性.

3.3 仿真结果

为了进一步检验基于 UTDU分解的改进方法的有效性,本文以我国的北斗卫星导航系统(COMPASS,BeiDou/COMPASSNavigation Satellite System)和美国的全球定位系统(GPS,Global Positioning System)组成的双星座组合导航系统为例进行了仿真分析.在实际使用中,用于表征伪距测量误差的用户等效距离误差(UERE,User Equivalent Range Error)可以近似表示为零均值高斯随机变量[1],统计表明,GPS单频接收机的典型伪距测量误差的标准差约为 6m[2],即用户等效距离误差的标准偏差 σUERE=6m.故在仿真中,以随机方式在伪距上施加了服从高斯分布 N(0,62)的误差.仿真结果表明,采用 UTDU分解方法和采用直接求逆方法进行 PVT求解和精度因子计算时,两者的求解结果完全一致,但如前所述,分解方法的计算量获得了较大改善.仿真结果统计表明,采用 UTDU分解方法进行 PVT解算时,位置偏差的均方差约为 6.11m,与输入的伪距测量误差基本相当,没有放大.图 3所示是仿真结果的位置误差分布图.

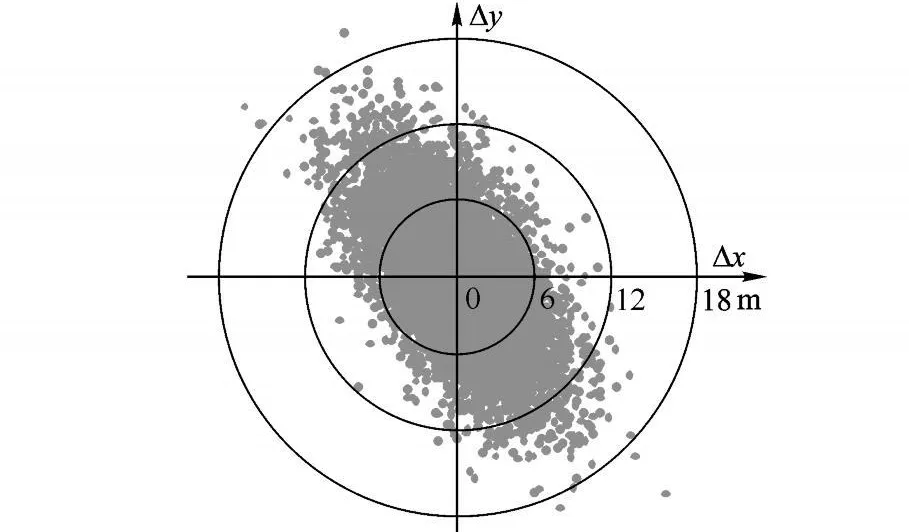
图 3 位置偏差

由图 3可见,在绝大部分情形下,位置偏差不超过 12m(即 2σUERE).统计表明,位置偏差不超过 2σUERE的时刻约为 96%,同时,解算的速度偏差也获得了类似的仿真结果,这就进一步表明了本文所述方法的正确性和有效性.另外需要说明的是,在测量矩阵严重病态时,因为分解方法有效降低了求解矩阵的病态性,所以,在数据精度有限的情况下,它能获得更为稳定的结果.当然,因为改进方法也只是最小二乘法的一种求解方法,最小二乘法的本质特征决定了其难以获得比测量误差更高的定位精度,要想获得更精确的定位结果,就需要采用合适的滤波方法.

4 结束语

在卫星导航定位系统中,进行精度因子计算和采用最小二乘法进行 PVT求解时,传统方法是基于测量矩阵的直接求逆来进行的.因为矩阵直接求逆的计算量较大,且在实际使用中,不可避免地会出现测量矩阵病态性较严重的情形,为了克服传统方法的不足,利用测量矩阵的对称正定性,以矩阵 UTDU分解为基础,提出了一种卫星定位求解和精度因子计算的改进方法,该方法有效降低了求解的计算量,并能有效降低求解矩阵的条件数,有效避免了在定位求解中因矩阵直接求逆带来的计算量大和数值稳定性差的问题.本文所提出的改进方法具有严格的数学理论基础,保证了方法的正确性和有效性.仿真结果也进一步验证了该方法的正确有效性.目前,该改进方法已经应用于所开发的 COMPASS和 GPS双星座兼容接收机中,所得结果满足了项目的要求.

References)

[1]Elliott D Kaplan,Christopher J Hegarty.GPS原理与应用[M].2版.寇艳红,译.北京:电子工业出版社,2007:36-472 Elliott D Kaplan,Christopher J Hegarty.Understanding GPS:principles and applications[M].2nd ed.Translated by Kou Yanhong.Beijing:Publishing House of Electronics Industry,2007:36-472(in Chinese)

[2]Pratap Misra,Per Enge.全球定位系统:信号、测量与性能[M].2版.罗鸣,等,译.北京:电子工业出版社,2008:22-69 Pratap Misra,Per Enge.Global positioning system:signals,measurements,and performance[M].2nd ed.Translated by Luo Ming,et al.Beijing:Publishing House of Electronics Industry,2008:22-69(in Chinese)

[3]谢钢.GPS原理与接收机设计[M].北京:电子工业出版社,2009:96-153 Xie Gang.Principles of GPS and receiver design[M].Beijing:Publishing House of Electronics Industry,2009:96-153(in Chinese)

[4]常青,柳重堪,张其善.GPS的几何精度因子和定位解的递推算法[J].通信学报,1998,19(12):83-88 Chang Qing,Liu Zhongkan,Zhang Qishan.The recurrence algorithm for GDOP and positioning solution in GPS[J].Journal of China Institute of Communications,1998,19(12):83-88(in Chinese)

[5]Bancroft S.An algebraic solution of the GPS equations[J].IEEE Transactions on Aerospace and Electronic Systems,1985,AES-21(1):56-59

[6]Krause L O.A direct solution to GPS-type navigation equations[J].IEEE Transactions on Aerospace and Electronic Systems,1987,AES-23(2):225-232

[7]Zhu Jijie.Calculation of geometric dilution of precision[J].IEEE Transactions on Aerospace and Electronic Systems,1992,28(3):893-895

[8]Shing H Doong.A closed-form formula for GPSGDOP computation[J].GPS Solutions,2009,13(3):183-190

[9]陈小平,滕云龙,康荣雷,等.几何精度因子改进算法研究[J].电子科技大学学报,2008,37(增刊):27-30 Chen Xiaoping,Teng Yunlong,Kang Ronglei,et al.Study of improved arithmetric of GDOP[J].Journal of University of Electronic Science and Technology of China,2008,37(suppl):27-30(in Chinese)

[10]Timothy Sauer.数值分析[M].吴兆金,等,译.北京:人民邮电出版社,2010:67-212 Timothy Sauer.Numerical analysis[M].Translated by Wu Zhaojin,et al.Beijing:Posts＆Telecom Press,2010:67-212(in Chinese)

[11]Steven J Leon.线性代数[M].7版.张文博,张丽静,译.北京:机械工业出版社,2007:286-319 Steven J Leon.Linear algebra with applications[M].7nd ed.Translated by Zhang Wenbo,Zhang Li jing.Beijing:China Machine Press,2007:286-319(in Chinese)

(编 辑 :娄 嘉)

Improved method of satellite positioning and dilution of precision

Chen Canhui Zhang Xiaolin

(School of Electronics and Information Engineering,Beijing University of Aeronautics and Astronautics,Beijing 100191,China)

In satellite navigation system,the traditional algorithm of solving dilution of precision(DOP)and satellite positioning based on least square method is the direct matrix inverse(DMI)method.In order to overcome the disadvantages of high computational burden and poor numerical stability of traditional DMI method,an improved method of satellite positioning and DOP was presented based on the matrix UTDU decomposition,which made use of the symmetric and positive definite performance of the measurement matrix.The correctness and validity of the new method can be guaranteed by the strict mathematical theory.The numerical results show that,in comparison with the traditional DMI method,the reduction of operational volume of positioning is about 60%and that of solving DOP is about36%by the proposed method.At the same time,the condition number of the solving matrix of the improved method has reduced considerably after decomposition and the numerical stability is significantly improved.

satellite navigation;leastsquare;solutions;dilution of precision(DOP);matrix decomposition

TN 967.1

A

1001-5965(2011)04-0472-06

2010-06-08

国防科工局航天民用专项资助项目;北京市重点学科基金资助项目(XK 100070525)

陈灿辉(1973-),男,湖南汨罗人,博士生,canhuich@yahoo.com.cn.