L-预拓扑空间的良紧性
王 瑜,马保国,张敏芝
(延安大学数学与计算机科学学院,陕西 延安,716000)
L-预拓扑空间的良紧性
王 瑜,马保国,张敏芝
(延安大学数学与计算机科学学院,陕西 延安,716000)
在 L-预拓扑空间中定义了良紧集,并讨论了 L-预拓扑空间中良紧集的等价刻划与基本性质。
L-预拓扑空间;α-远域族;良紧集;r-覆盖;α-网
众所周知,紧性理论是模糊拓扑学研究的重要课题之一,而良紧性被认为是一种最好的紧性。文献[1]王国俊教授在 LF-拓扑空间中,就 L=[0,1]的情形引入良紧性理论。彭育威在文献[2]、[3]中将良紧性理论推广到一般的F格 L的情形,给出了不依赖于[0,1]拓扑结构的良紧性的等价刻划,并讨论了它们的基本性质。自从李生刚等人在文献[4]中引入L-预拓扑空间的概念以来,得出了一系列有意义的结果[4-7]。但是在 L-预拓扑空间,对于良紧集目前还没有研究。因此本文的主要目的是在已有文献的基础上,引入 L-预拓扑空间的良紧集及良紧空间的概念,给出了它们的等价刻划并研究其基本性质,如,L-预拓扑空间的良紧性对闭子集是遗传的、弱拓扑不变的、L-好的推广等。
本文中L表示具有最小元0和最大元 1的De Morgan代数,LX是从 X到 L的映射的全体。Copr(L)表示L中非 0余素元的全体,Pr(L)表示 L中非1素元的全体。α∈L,β(α)为α的极小集,β*(α)=β(α)∩Copr(L).其它记号和术语见参考文献。
1 预备知识
定义 1.1[4]设L是 Fuzzy格,X≠∅,δ⊂LX,

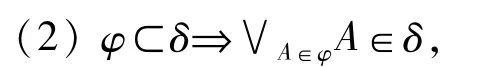
若则称δ为X上的L-预拓扑,称(X,δ)为L-预拓扑空间,δ中的成员称为 L-开集,δ′中的成员称为 L-闭集。
定义 1.2[6]设(X,δ)是L-预拓扑空间,xλ∈Copr(LX),A∈δ′,若 xλ≤A,则称A为xλ的闭预远域。设 B∈LX,若有 xλ的闭预远域 A,使得 B≤A,则称B为xλ的预远域。xλ的所有预远域之集,称为 xλ在(X,δ)中的预远域系,记作 ηδ(xλ);xλ在
定义 1.3[5]设(X,δ)是L-预拓扑空间,G∈LX,α∈Copr(L),Φ⊂δ′。
(1)若∀xa≤G,存在 A∈Φ,使得 xa≤A,则称Φ为 G的 α-预远域族。记作∧Φ<G(α)。
(2)若∃γ∈β*(α),使 Φ为 G的 γ-预远域族,则 称 Φ 为 G的 α--预远 域族,记 作∧Φ<<G(α)
定义 1.4[6]设(X1,δ1)和(X2,δ2)为两个L-预拓扑空间,f:X1→X2是一个映射,如果对任意 B∈δ2,有fL←(B)∈δ1,或对任意 B∈δ2′,有 fL←(B)∈δ1′,则称 f为连续的 L-值 Zadeh型函数。
其中,fL→

定义1.5 设(X,δ)是L-预拓扑空间,α∈Copr(L),称X中网{S(n),n∈D}为α-网,是指存在n0∈D,使得对于任意n≥n0(n∈D),当r∈β*(α)时,有V(S(n))≥r成立。其中V(S(n))表示S(n)的高度,令V(S)={V(S(n)),n∈D},这时V(S)是 L中的分子网,称为 S的值网。
定义1.6 设S={S(n),n∈D}为L-预拓扑空间(X,δ)中的α-网,xα∈Copr(LX),如果∀U∈ηδ(xα),S经常不在U中,则称 xα为 S的聚点。
定义 1.7[6]设(X,R)是分明的预拓扑空间,L是完全分配格,A:X→L是映射。如果对任意的 α这里 R′表示(X,R)中全体闭集之族。则称 A为 X上的 L值下半连续映射。以 ωL(R)表示X上全体下半连续映射之集,则
(1)X上每个 L中取常值的函数属于ωL(R),
(2)若A,B∈ωL(R,则A∧B∈ωL(R),
(3)若I⊂ωL(R),则∨I∈ωL(R).
由此可见,ωL(R)是 X上的 L-预拓扑,叫做由R生成(或诱导)的 X上的 L-预拓扑,并且称(X,ωL(R)为(X,R)拓扑生成(或诱导)的L-预拓扑空间。
2 L-预拓扑空间的良紧集
定义2.1 设(X,δ)是L-预拓扑空间,A∈LX.如果对 A的任一α-预远域族 Φ⊂δ′,Φ有有限子族 Ψ,使 Ψ构成 A的α--预远域族,则称A为(X,δ)中的良紧集。
当(X,δ)中的最大L-集1是良紧集时,称(X,δ)为良紧的L-预拓扑空间,简称良紧空间。
定理2.1 设(X,δ)是L-预拓扑空间,A∈LX,则 A为良紧集当且仅当以下条件成立:
(1)∀α∈Copr(L),A的每个 α-预远域族 Φ都有有限的子 α-预远域族,即,若∧Φ<A(α),则有 ψ∈2(Φ),使∧Ψ<A(α).
(2)∀α∈Copr(L),由一个闭集构成的 A的α-预远域族 Φ={P}也是 A的 α--预远域族。
证明 必要性:设 A是良紧集,∀α∈Copr(L),Φ是A的α-预远域族,则Φ有有限子族 Ψ,使∧Ψ<<A(α).这时自然有∧Ψ<A(α),即,Ψ是 Φ的有限子 α-预远域族,从而(1)成立。再设Φ={P}是 A的α-预远域族,则 Φ有有限子族,使∧Ψ<<A(α).但这时只可能 Ψ=Φ,所以,Φ也是A的α-的任一分子 xr,均有这时,存在Q∈Ψ,使r≤Q(x),所以,Ψ是A的 α--预远域族。这就证明了 A是良紧集。
定义2.2 设(X,δ)是L-预拓扑空间,Ω⊂LX.如果∨Ω=1,则称Ω为(X,δ)的覆盖。如果 Ω⊂δ,则称Ω为(X,δ)的开覆盖。当 Δ⊂Ω,且∨Δ=1时,称 Δ为 Ω的子覆盖。
定义2.3 设(X,δ)是L-预拓扑空间,Ω⊂δ,r是L中的素元,且r<1。∀x∈X,有U∈Ω,使U(x)≤r,则称 Ω为(LX,δ)的r-覆盖,或简称 Ω为r-覆盖。设 α*(r)是 r的异于1的素元组成的极大集。若存在s∈α*(r),使Ω为(X,δ)的s-覆盖,则称Ω为 r+-覆盖。
定理2.2 L-预拓扑空间(X,δ)是良紧集当且仅当每个r-覆盖Ω,都有有限子族 Δ,使 Δ构成r+-覆盖。
证明 设(X,δ)是良紧空间,Ω是 r-覆盖,r是 L中的素元且 r<1.令Φ=Ω′,则 Φ是闭集族,且∀x∈X,有P=U′∈Φ,使U(x)≤r,也就是r′≤P(x).因为r是异于1的素元,所以 r′是 L中的分子。由xr
′≤P知,P∈ηδ(xr′).这表明 Φ是 r′-预远域族,因为(X,δ)是良紧空间,所以,Ω有有限子族Δ,使得 Ψ=Δ′构成(r′)--预远域族,即,存在 s∈β*(r′),使得∀x∈X,有B∈Δ,使s≤V′(x).这等价于存在s′∈α*(r),使∀x∈X,有 B∈Δ,使V(x)≤s′.可见Ω的有限子族 Δ是 r+-覆盖。
反过来,设(X,δ)的每个 r-覆盖都有有限子族构成(X,δ)的 r+-覆盖。设 Φ是任一 α-预远域族。令Ω=Φ′,r=α′,则由α为分子知r是异于1的素元且 Ω是 r-覆盖。由假设Ω有有限子族 Δ,使其构成 r+-覆盖,令 Ψ=Δ′,则Ψ是Φ的有限子族。易证 Ψ是α--预远域族,所以(X,δ)是良紧空间。
定理2.3 设(X,δ)是L-预拓扑空间,A∈LX,则 A是良紧集当且仅∀α∈Copr(L),A中的α-网在 A中有一高度等于 α的聚点。
证明 设 A是良紧集,S={S(n),n∈D}是 A-预远域族,从而(2)成立。
充分性:设条件(1)和(2)成立,∀α∈Copr(L),Φ是A的 α-预远域族。由(1)知,Φ有有限子族Ψ,使∧Ψ<A(α).令P=∧Ψ,则{}P显然是A的 α-预远域族。由(2)知,{ }P也是A的 α--预远域族。即,Copr(L)中有分子r∈β*(α),使得对A中中的 α-网,若S在 A中没有高度等于α的聚点。那么,对A中任一分子 xα,有U(x)∈ηδ(xα)使 S最终小于或等于U(x),即,存在n(x)∈D使当n≥n(x)时S(x)≤U(x).令},则Φ是A的 α-远域族。因为 A是良紧集,Φ有有限子族 Ψ使∧Ψ<<A(α),即,存在r∈β*(α)使得对 A中任一分子yr有i≤k使 yr≤U(xi).令,则对 A中任一分子yr有 yr≤ U,即,

因为 D是定向集,存在 n0∈D使 n0≥n(xi)(i=1,...,k)。那么当 n≥n0时,S(n)≤U(xi)(i=1,...,k),从而当n≥n0时S(n)≤U,即,

由(1),(2)式及S(n)≤A得,当n≥n0时 V(S(n))≥r。这与S是A中的 α-网的定义相矛盾。所以S在 A中至少有一高度等于 α的聚点。
反过来,设 A中每个α-网在 A中有高度等于α的聚点(α∈Copr(L)),Φ是A的 α-远域族。设Φ的任一有限子族 Ψ都不是A的 α--远域族,则∀Ψ∈2(Φ),∀r∈β*(α),A中有分子xΨ
r使

令 D=β*(α)×2(Φ),对 D中二元(r1,Ψ1)与(r2,Ψ2),规定(r1,Ψ1)≤(r2,Ψ2)当且仅当 r1≤r2且 r1≤r2,
由[1]中的引理6.2.6易知 D是定向集。令

则S是 A中的分子网。因为∀r∈β*(α),任取Ψ0∈2(Φ),则当(s,Ψ)≥(r,Ψ0)时,V(xΨs)≥r,所以 S是A中的α-网。在 A中任取高度等于 α的分子 xα.由 Φ是A的 α-远域族知,有Q∈Φ使 Q∈ηδ(xα).这时{Q}∈2(Φ).任取s∈β*(α),则当(r,Ψ)≥(s,{Q})时,由(3)式及Q∈Ψ知≤Q,即,S最终在Q中,所以 xα不是 S的聚点。那么 S在 A中就没有高度等于 α的聚点,此与题设矛盾。所以 Φ有有限子族 Ψ,使 Ψ成为A的α--远域族,可见 A是良紧集。
定理2.4 设(X,δ)是L-预拓扑空间,A是良紧集,B是闭集,则 A∧B是良紧集。
证明 设S是A∧B中的α-网,则S也是A中的 α-网。因为 A是良紧集,S在 A中有一高度等于 α的聚点 xα。但 S又是闭集 B中的分子网,xα作为 S的聚点应当有 xα≤B1。所以 xα≤A∧B,即,xα是 S在 A∧B中的聚点,因此A∧B是良紧集。
L-预拓扑空间中的良紧集在连续的 L值 Zadeh型函数之下的像是良紧集。
定理2.5 设(X1,δ1)和(X2,δ2)是L-预拓扑空间,f:(X1,δ1)→(X2,δ2)是连续的L值Zadeh型函数,那么当 A是(X1,δ1)中的良紧集时f(A)是(X2,δ2)中的良紧集。
证明 ∀α∈Copr(L),设 Φ是f(A)的 α-预远域族,则对 A中任一分子 xα,f(xα)=(f(x))α是 f(A)中高度等于α的分子,所以Φ中有闭集 P,使(f(x))α≤P,或 α≤P(f(x)),这等价于α≤f-1(P)(x)或xα≤f-1(P)。因为f连续,f-1(P)是(LX,δ1)中的闭集,所以,f-1(P)∈η-δ1(xα),从而f-1(Φ)是A的α-预远域族。由 A的良紧性知,Φ有有限子族 Ψ={P1,...,Pn},使f-1(Ψ)是A的α-预远域族。以下只须证明Ψ就是 f(A)的α--预远域族,为此只须证明存在s∈β*(α),使 f(A)中任一高度等于s的分子ys而言,存在 i≤n使ys≤Pi,即,只须证明事实上,由 f-1(Ψ)是 A的α--预远域族知,有 r∈β*(α),使对 A中任一分子 xr和 i≤n,都有 xr≤f-1(Pi),即,


现在设(4)不成立,即,

因为α=sup*(α),所以由极小映射 β的性质知

由r∈β*(s)知,有x∈X使A(x)≥r且f(x)=y。这时xr是A中的分子,从而满足(5)。又,(f(x))r=yr≤ys,所以由(6)得 f(xr)=(f(x))r=yr≤P1∧...∧Pn。即

上式与(5)相矛盾,所以(4)式成立。
推论 2.1 L-预拓扑空间中良紧性是弱拓扑不变的。
定理2.6 设(X,ωL(R))是由分明预拓扑空间(X,R)拓扑生成的 L-预拓扑空间,则(X,ωL(R))是良紧空间当且仅当(X,R)是紧空间。
证明 必要性:设(X,ωL(R))是良紧空间,Ψ是(X,R)的开覆盖。令

则 Γ是(X,ωL(R))中的开集族。由L的最大元1可表示为若干分子之并。任取这样一个分子 α,令 r=α′,则 r是异于1的素元,这时 Γ显然是r-覆盖。由(LX,ωL(R))的 良 紧 性知,Ψ有有 限 子族{W1,...,Wn}使 Γ 的有 限 子族 Δ = {χWi成为 r+-覆盖。那么对每个 x∈X,有 χWi∈Δ,使 χWi(x)≠0,即,x∈Wi.可见{W1,...,Wn}是Ψ的有限子覆盖。所以(X,R)是紧空间。
充分性:设(X,R)是紧空间,Σ是(LX,ωL(R))是r-覆盖,∀x∈X,可取Ux∈Σ,使Ux(x)≤r,所以有s(x)∈α*(r),使Ux(x)≤s(x).这时


因为 Ux是 X上的L值下半连续函数组成,ιs(x)(Ux)是(X,R)中的开集,所以,是(X,R)的开覆盖。因为(X,R)是紧空间,故有x1,...,xn∈X,使得构成Γ的有限子覆盖,由文献[1]的引理6.2.6易知,α*(r)是下定向集,所以,存在s∈α*(r),使 s≤s(x1),...,s≤s(xn).任取x∈X,由 Γ0是X的覆盖知有 i<n,使得 x∈ιs(xi)(Uxi),从而 Uxi(x)≤s(xi),那么更有 Uxi(x)≤s.这表明Γ0是 s-覆盖,从而,Γ0是r+-覆盖。由定理2.2知,则(X,ωL(R))是良紧空间。
推论2.2 L-预拓扑空间中良紧性是 L-好的推广。
[1]王国俊.L-fuzzy拓扑空间论[M].西安:陕西师大出版社,1988:94.
[2]彭育威.L-fuzzy拓扑空间的良紧集[J].数学学报,1986,29(4):555-558.
[3]彭育威.L-良紧子集的刻划[J].数学进展,1987(16):87-90.
[4]苏华飞,李生刚.L-预拓扑的确定[J].内蒙古大学学报(自然科学版),2006,37(4):378-381.
[5]钟晓静,尤飞,李生刚.L-预拓扑空间中模糊网的 O-收敛及其应用[J].模糊系统与数学,2010,24(1):35-40.
[6]贺晓丽,伏文清.L-预拓扑空间的局部连通性:可乘性与 L-好的推广[J].山东大学学报,2010,45(10):78-82.
[责任编辑 贺小林]
N-Com pactness In L-Pretopological Spaces
WANG YU,MA Bao-guo,ZHANG Min-zhi
(College of Mathematics and Computer Science,Yan an University,Yan an 716000,China.)
The conceptof N-compactnesswas defined in L-pretopological spaces,two characterization of the ncompactnesswere given,and some of its importantwere discussed.
L-pretopological spaces;N-compactness;α-remote neighborborhood;r-covered set;α-net
O189.1
A
1004-602X(2011)02-0009-04
2011 -05 -03
陕西省自然科学基金青年资助项目(2010JQ1005)
王瑜(1985—),女,陕西乾县人,延安大学在读硕士研究生。

