切割函数关于第二参数的分析性质
岳崇山
(河北北方学院理学院,河北 张家口075000)
双切圆技术是考察区域的边界曲线的对称性的一种重要的方法.现在,许多文献已经对曲线的双切圆进行了细致的研究,文献 [1]中Peter J.Gibin和S.A.Brassett讨论了平面闭曲线的双切圆的存在性问题;文献 [2]中Peter J.Gibin和Donal B.O’shea又对双切圆问题的高维情形进行了进一步的推广.在平面曲线的双切圆问题中,切割函数是一个重要工具.文献 [3-6]从各种角度研究了切割函数的一些基本的性质,特别是文献 [6]讨论了平面曲线的切割函数对参数s的连续性和可导性.本文将讨论切割函数对第二参数的连续性和可导性.
1 基本概念
约定r⇀(s)为平面上的Cm(m≥2)类正则曲线,参数s为弧长.定义一个集合

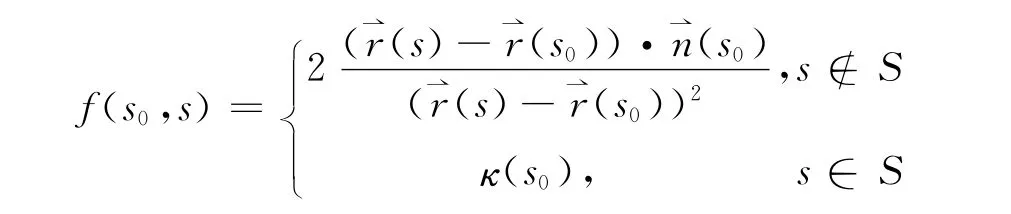
2 主要结果
先来考察平面曲线的切割函数对第二参数s0的连续性.
定理1 平面曲线的切割函数关于第二参数s0是连续函数.
证明 f(s0,s)是平面曲线(s)的切割函数.只需说明s0∈S是f(s0,s)的可去间断点.不妨设(s0)→(s)时,s0→s.此时,切割函数f(s0,s)的分子分母都趋于零,故可以考虑使用罗比达法则.
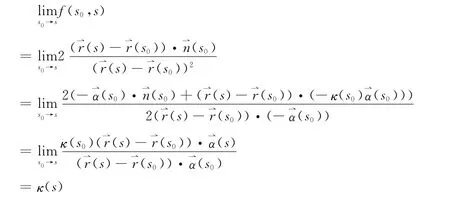
即f(s0,s)关于参数s0是连续函数.这样,如果视切割函数为二元函数的话,切割函数是连续的.
下面的定理考察了平面曲线切割函数关于第二参数s0的可导性.
定理2 如果平面曲线关于参数s0是Cm(m≥2)类的,那么适当地补充值之后,其切割函数关于第二参数s0是C(m-2)类的.
证明 当s∉S时,由于平面曲线r⇀(s)是Cm类的,而其切割函数的表达式为

故此时f(s0,s)关于第二参数s0也是Cm类的.
下面研究f(s0,s)在s0∈S处的可导性.


由于新的表达式中,分子分母都是关于第二参数s0C(m-2)类的,且分母有意义,故适当地补充值可以使得切割函数f(s0,s)是关于第二参数s0C(m-2)类的.
由定理1和定理2立即可得下面的推论.
推论1 如果平面曲线是光滑的,那么其切割函数对关于第二参数s0是光滑的.
结合文献 [6]的结果,由推论1还可以得到平面曲线的切割函数的非常好的结果.
定理3 如果平面曲线是光滑的,那么其切割函数关于参数s0和参数s都是光滑的.
[1] Giblin PJ,Brassett SA.Local sy mmetr y of plane curves[J].Amer Mat h Month,1985,(92):689-707
[2] Gibin PJ,O'shea DB.The bitangent sphere problem [J].Amer Math Month,1990,97 (01):5-23
[3] 岳崇山,宋旭华.切割函数为常值的曲线的一个结果 [J].河北北方学院学报:自然科学版,2010,26(03):13-15
[4] 岳崇山.切割函数的运动不变性 [J].河北北方学院学报:自然科学版,2010,26(05):10-13
[5] 岳崇山,张蒲修.切割函数与参数选择的关系 [J].河北北方学院学报:自然科学版,2011,27(05):10-12
[6] 岳崇山,宋旭华,景海斌.平面曲线的切割函数的分析性质 [J].河北北方学院学报:自然科学版,2010,26(04):14-16

