一种调和Ritz向量的精化算法及应用
肖小花 戴 芳 郭文艳
(西安理工大学理学院,西安710054)
在大量的应用科学和工程计算中,如计算流体力学、量子物理、化学工程、经济模拟、材料科学、结构工程和网络排队的Markov链模拟等领域,许多问题最后都归结为大规模矩阵特征值问题。由于大规模矩阵的阶数很高,而且往往是稀疏矩阵,直接求解其全部特征值不太现实,在实际中需要的往往只是矩阵的部分特征对。近几年来,大规模矩阵的内部特征值问题在许多实际问题中的应用越来越多,成为一个新的研究热点。
Scott提出的位移求逆的Arnoldi方法对于大规模矩阵内部特征值问题的求解是非常有效的[1]。该方法能够达到很快的收敛速度,但由于计算过程中需要对大规模矩阵进行分解,这一方面会破坏原矩阵的稀疏结构,增加存储量;另一方面,由于Arnoldi算法在迭代过程中对矩阵的扰动是非常敏感的[2],而求逆过程又很难保证达到可靠的精度,因此这种方法被认为不实用。由Morgan[3,4]提出的调和 Arnoldi方法目前被认为是解大规模矩阵内部特征问题最有效的方法之一[5],已成为一种更为实用的求解方法。
本文利用调和Arnoldi算法的一种等价形式来求解调和Ritz对,并应用精化Arnoldi算法的思想给出了一种精化变形,进一步对调和Ritz向量进行精化求解,寻求使残量范数达到极小的近似特征向量,并对这种方法进行了理论分析,给出了数值实验。理论分析显示了这种方法的可行性,数值实验显示这种方法的优越性。最后将本文的算法应用于K-L变换的变换矩阵求解中。K-L[6]变换的核心过程是计算特征值和特征向量。由于待处理矩阵维数高,一般的方法很难求出其特征值及特征向量,甚至无法求出。K-L变换的一些优化处理过程复杂,很难满足实时性的要求,使得用K-L变换进行图像压缩难以广泛应用。而本文的算法正好就是一种快速求解大规模矩阵特征值及特征向量的方法,将其用于K-L变换来进行图像压缩是可行的。
1 调和Arnoldi方法的一种实现形式
对于任意给定的单位初始向量q0∈Rn和实定点τ,构造m维的Krylov子空间
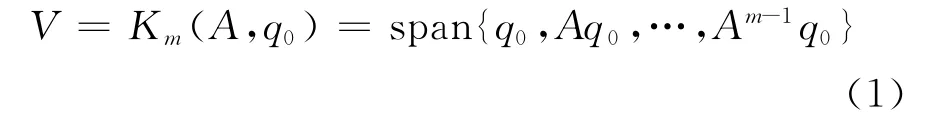
用Q表示V的位移子空间,即Q=(A-τI)V ,所以有
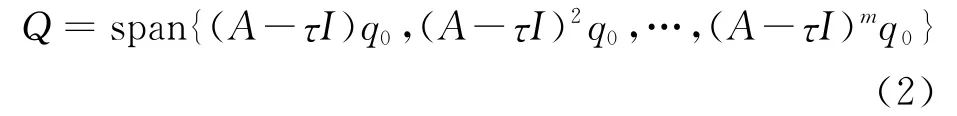
设dimV=dimQ=m,令r11=‖(A-τI)q0‖,q1= (A-τI)/r11,则有
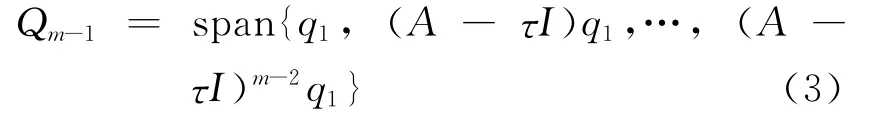
用Arnoldi过程生成Qm-1的一组标准正交基,记Qm-1= [q1,q2,…,qm-1],Qm= [Qm-1,qm],这一过程可以用矩阵形式表示成
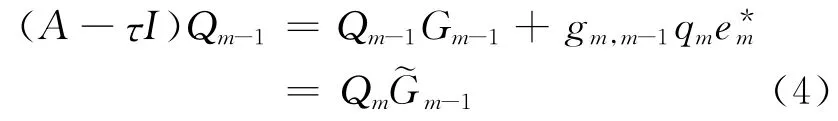
其 中 Gm= (gij)m×m和 Rm= (rij)m×m均为上Hessenberg矩阵,则q1,…,qm构成了Q 的一组标准正交基。我们将上述产生Q的一组标准正交基的过程称为位移Arnoldi过程[7]。
从上面的叙述可以得出:
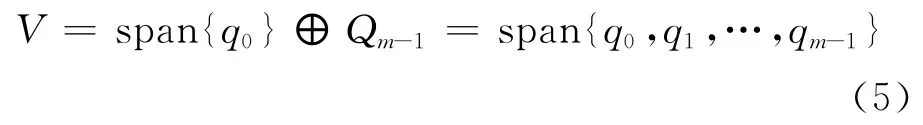
q0,q1,…,qm-1构成了V 的一组基,令Um= [q0,q1,…,qm-1],则由位移 Arnoldi过程可得
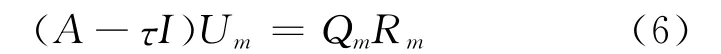
其中Qm= [q1,…,qm]。关系式(6)揭示了子空间Q的一组标准正交基Qm和V的一组基Um之间的关系。
利用上述的位移Arnoldi过程和调和投影得特征值问题[3,8]
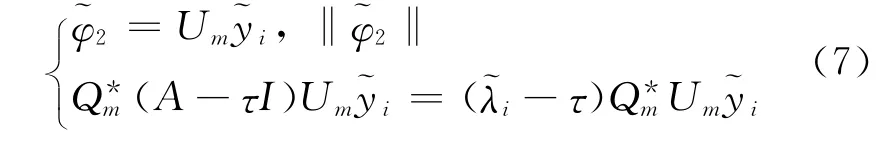
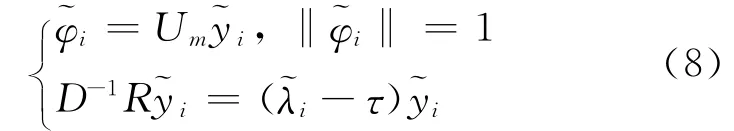
2 调和Ritz向量的精化变形算法
用调和投影方法来解决大规模矩阵的部分内部特征值问题时,理论分析表明Ritz向量的收敛条件更严格,往往调和Ritz值作为特征值的近似非常适合,而相应的调和Ritz向量近似程度很差。Jia提出了对于确定的特征值,在近似特征向量的计算上使用满足某种最优条件的精化近似向量来代替传统的Ritz向量或者调和Ritz向量[9,10],分析表明精化近似特征向量能够从理论上克服调和Ritz值收敛到特征值时,调和Ritz向量经常不收敛的问题;同时,他还证明了当使用精化调和Ritz向量来作为特征向量的近似时,能够得到与相应的Ritz值相同的收敛性。本文利用位移Arnoldi算法生成的位移Krylov子空间,结合精化的思想给出一种精化变形,在位移Krylov子空间中进行正交投影来对调和Ritz向量进行精化求解,使改进后调和Ritz向量对应的残量范数在求解空间上达到极小。
由前文的介绍可知,位移Krylov子空间Q为m维,则在Q上进行正交投影
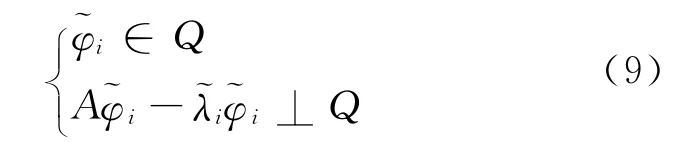
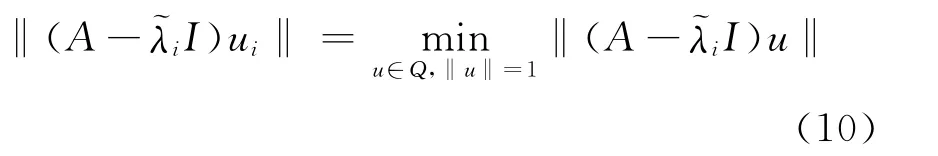
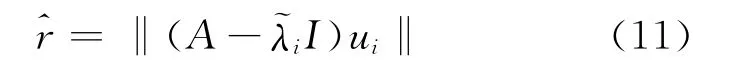
根据精化思想,并由关系式(6)和(10),有以下关系式成立
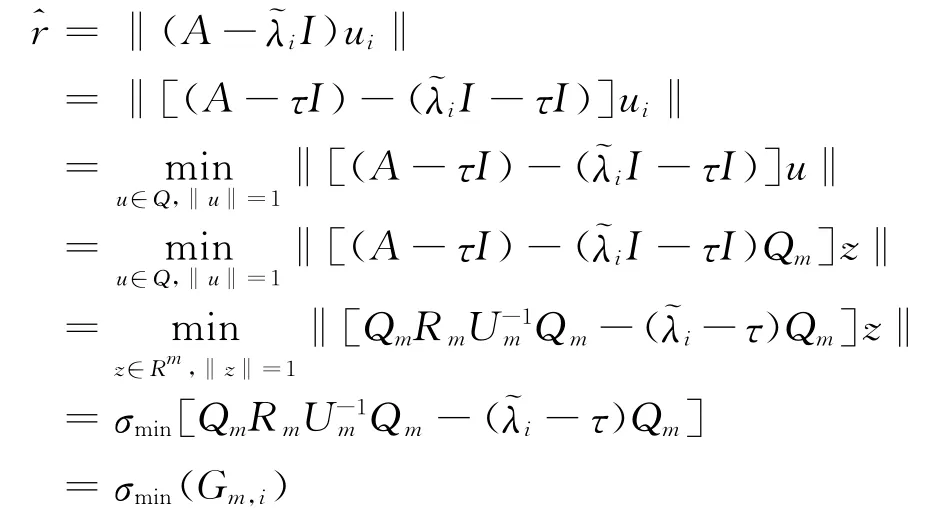
结论:若zi是矩阵Gm,i的最小奇异值σmin(Gm,i)所对应的右奇异向量,且ui=Qmzi,那么,其中-τ)Qm。
由式(10)可知这种精化变形使调和Ritz向量对应的残量范数在求解空间上达到极小,若设,则,因此精化变形方法比原来的方法能达到更好的收敛性质和更快的收敛速度。下面给出调和Ritz向量的精化变形算法。
(1)给定子空间维数m,需要计算的特征向量的个数k以及要求达到的精度tol,选择一个单位初始向量q0。
(2)生成子空间Q的一组标准正交基向量,得到Um,Qm,Rm。
(3)计算近似特征对。通过式(8)计算近似特征对作为A的特征值的近似,利用ui=Qmzi计算精化后的调和Ritz向量,按要求从中选择k个作为准确特征对 (λi,φi)的近似(i=1,2,…,k),其 中zi为 矩 阵Gm,i的 最 小 奇 异 值σmin(Gm,i)所对应的右奇异向量;
(5)重新启动。构造新的初始向量q0,转向第(2)步。
注:算法第(5)步采用显式重新启动策略,即重新启动后的初始向量q0取作
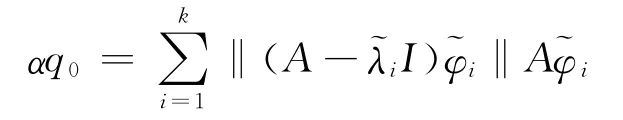
其中α为规范化因子。
3 数值算例与实验结果
3.1 数值算例
在INTEL PENTIUM微机上使用MATLAB7.0软件包对本文的整个算法进行数值实验。算法中停机准则设为,实验中设精度为tol,当stopcrit≤tol时停机。数值实验中所用的大规模矩阵为图像矩阵,图像为图1和图2所示的以jpg文件格式存储的山水和松树,山水的大小为1 000×1 000,松树的大小为2 000×2 000。

图1 山水Fig.1 Landscape

图2 松树Fig.2 Pine
数值算例1以图1的图像矩阵作为待计算特征值和特征向量的矩阵,矩阵的规模为1 000×1 000。m表示Krylov子空间的维数,m分别取10、20和30;n表示重新启动的次数;t表示运算时间,以秒为单位;M表示矩阵与向量乘积的个数。“-”表示算法200步迭代未收敛。tol=10-7,位移τ=1,初始向量q0是按均匀分布生成的随机向量。按本文算法计算得到矩阵按实部最大的3个特征值依次近似为λ1≈14.423 5,λ2≈10.211 8,λ3≈8.367 3。按调和 Arnoldi算法的等价变形计算得到矩阵按实部最大的3个特征值依次近似为λ1≈14.393 2,λ2≈10.192 6,λ3≈8.287 5。表1给出了计算的结果。
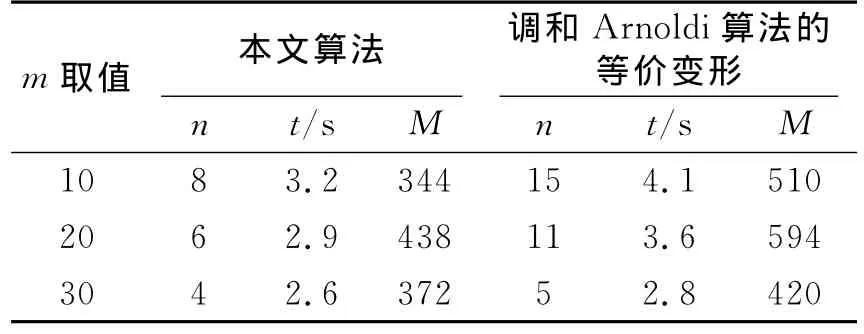
表1 对1 000阶方阵用不同方法计算的结果比较Table 1 Comparison of the calculated results of 1 000 order matrixes by different methods
数值算例2此例是以图2的图像矩阵作为待计算特征值和特征向量的矩阵,矩阵的规模为2 000×2 000。m,τ,q0的取值同数值算例1,精度tol=10-6。按本文算法计算得到矩阵按实部最大的3个特征值依次近似为λ1≈15.358 1,λ2≈12.807 9,λ3≈10.394 2。按调和Arnoldi算法的等价变形计算得到矩阵按实部最大的3个特征值依次近似为λ1≈15.317 2,λ2≈12.799 1,λ3≈10.295 5。表2给出了计算的结果。
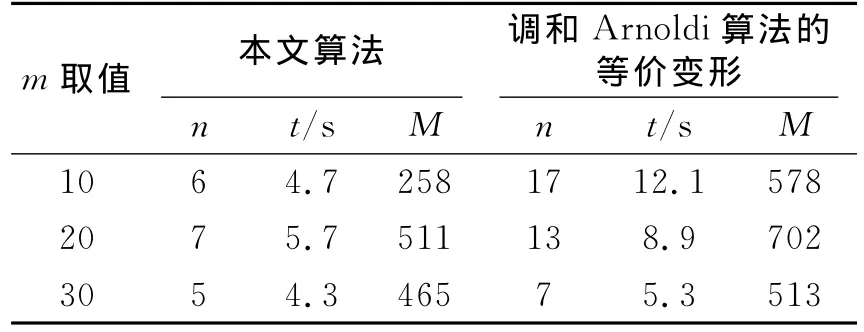
表2 对2 000阶方阵用不同方法计算的结果比较Table 2 Comparison of the calculated results of 2 000order matrixes by different methods
由以上2例的计算结果可以得出:对于不同的子空间维数,本文算法更有效,无论是在运算时间还是在达到收敛时的迭代步数上均优于精化前的调和Arnoldi算法;特别是当子空间维数越小时,达到收敛迭代的步数更少,计算所需的时间更短,优越性更明显。
3.2 实验
在用K-L变换对图像进行压缩的实验中,考虑到计算机处理器的性能,本文采用了如下方法:首先把图像矩阵分成了大小相同的几个矩阵,再用本文算法算出每个矩阵的协方差矩阵的特征值和特征向量,进而对每个矩阵进行K-L变换,并把变换后得到的每个压缩图像矩阵相应地合成为压缩后的整幅图像矩阵,最后显示出压缩后的整幅图像。如果计算机处理器的性能比较好,则用本文的算法就可以直接计算整幅图像矩阵的协方差矩阵的特征值和特征向量,对整幅图像矩阵进行K-L变换来压缩图像。对于将图像分成若干小块而对每个小块分别进行K-L变换的方法,一般选择大小为8×8的块。
实验1对大小为256×256×8bit的以png文件格式存储的米粒灰度图像进行压缩。我们比较了以下2种方法:第一种是本文的图像压缩方法,将图像矩阵分成16个64×64的方阵。第二种是将图像分成若干小块而对每个小块分别进行变换的方法[11],记为JK-L,每个小块选为8×8。t表示算法的执行的时间(以分钟为单位)。在实验中,本文的算法选取Krylov子空间的维数m=30。对特征值的保留个数分别取为1、2、4、8、16,将特征向量量化为8位二进制数,用2种方法分别进行测试的情况如表3所示。
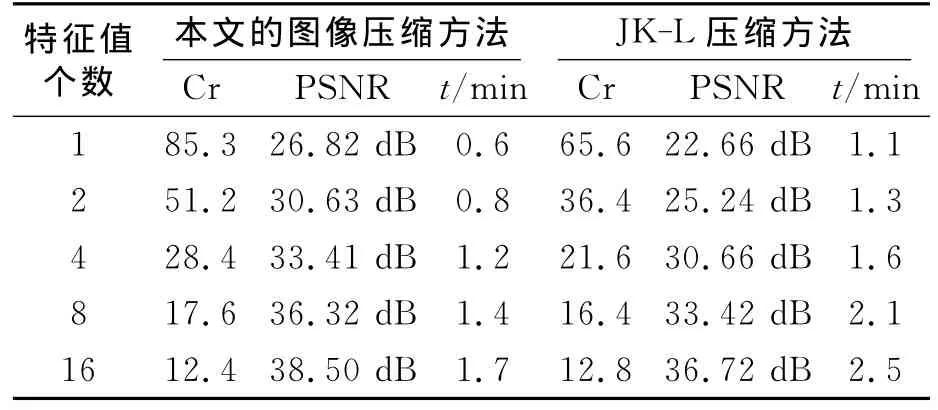
表3 256×256×8bit图像的压缩比和峰值信噪比及算法执行时间Table 3 256×256×8bit image compression ratio and peak signal/noise ratio and the algorithm time
用本文方法对米粒图进行压缩的原图和保留特征值个数分别为1、2、4、8、16的压缩后的重建图像如图3所示。
将图像分块的JK-L方法对米粒图进行压缩的原图和保留特征值个数分别为1、2、4、8、16的压缩后的重建图像如图4所示。
实验2对大小为512×512×8bit的以jpg文件格式存储的牵牛花灰度图像进行压缩。比较了以下2种方法:第一种是本文的图像压缩方法,将图像矩阵分成16个128×128的方阵。第二种是将图像分成若干小块而对每个小块分别进行变换的方法,记为JK-L,每个小块选为8×8。t表示算法的执行时间(以分钟为单位)。在实验中,本文的算法选取Krylov子空间的维数m=30。对特征值保留个数分别取为1、2、4、8、16,将特征向量量化为8位二进制数,用2种方法分别进行测试的情况如表4所示。

图3 米粒的原图及保留特征值的重建图像Fig.3 Original image of rice and the reconstructed image of the eigenvalue

图4 米粒原图及保留特征值的重建图像Fig.4 Original of rice image and the reconstructed image of the eigenvalue
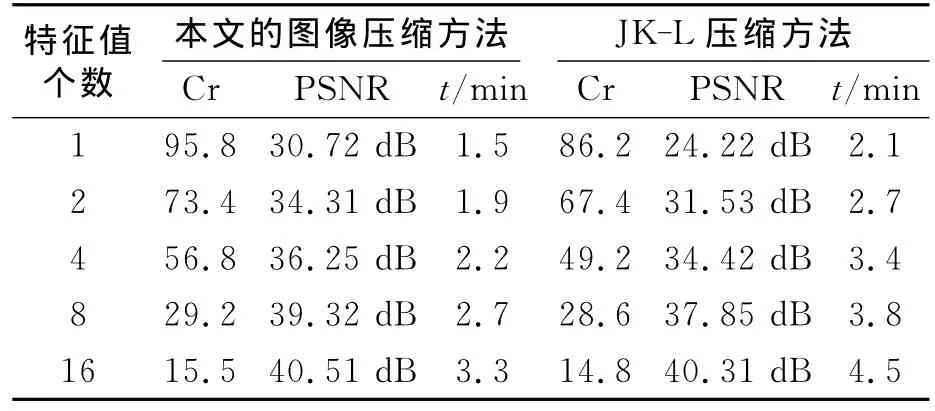
表4 512×512×8bit图像的压缩比和峰值信噪比及算法执行时间Table 4 512×512×8bit image compression ratio and peak signal/noise ratio and the algorithm time
用本文方法对牵牛花图进行压缩的原图和保留特征值个数分别为1、2、4、8、16的压缩后的重建图像如图5所示。
将图像分块的JK-L方法对牵牛花图进行压缩的原图和保留特征值个数分别为1、2、4、8、16的压缩后的重建图像如图6所示。
从以上2个实验的结果可以看出:从压缩比、峰值信嗓比以及算法的执行时间上,用本文的方法来使用K-L变换进行图像压缩要优于将图像数据矩阵分成若干小块而在每个小块上使用K-L变换的方法。
4 结束语
本文研究了大规模矩阵特征值问题的一种数值求解方法,对调和Arnoldi方法进行了改进,在精化思想的基础上给出了一种精化变形方法。保持调和Ritz值不变,对调和Ritz向量进行了精化求解,理论分析和数值实验结果均表明了该方法的可行性及有效性,并将其用于K-L变换进行图像压缩。这种将大规模矩阵特征值问题的数值求解方法引入K-L变换来进行图像压缩,解决了KL变换中变换矩阵过大而求解困难的问题。进一步对大规模矩阵特征值问题数值求解方法的研究,将有助于用K-L变换对图像进行实时压缩和传输。

图5 牵牛花的原图及保留特征值的重建图像Fig.5 The original image of morning glory and the reconstructed image of the eigenvalue
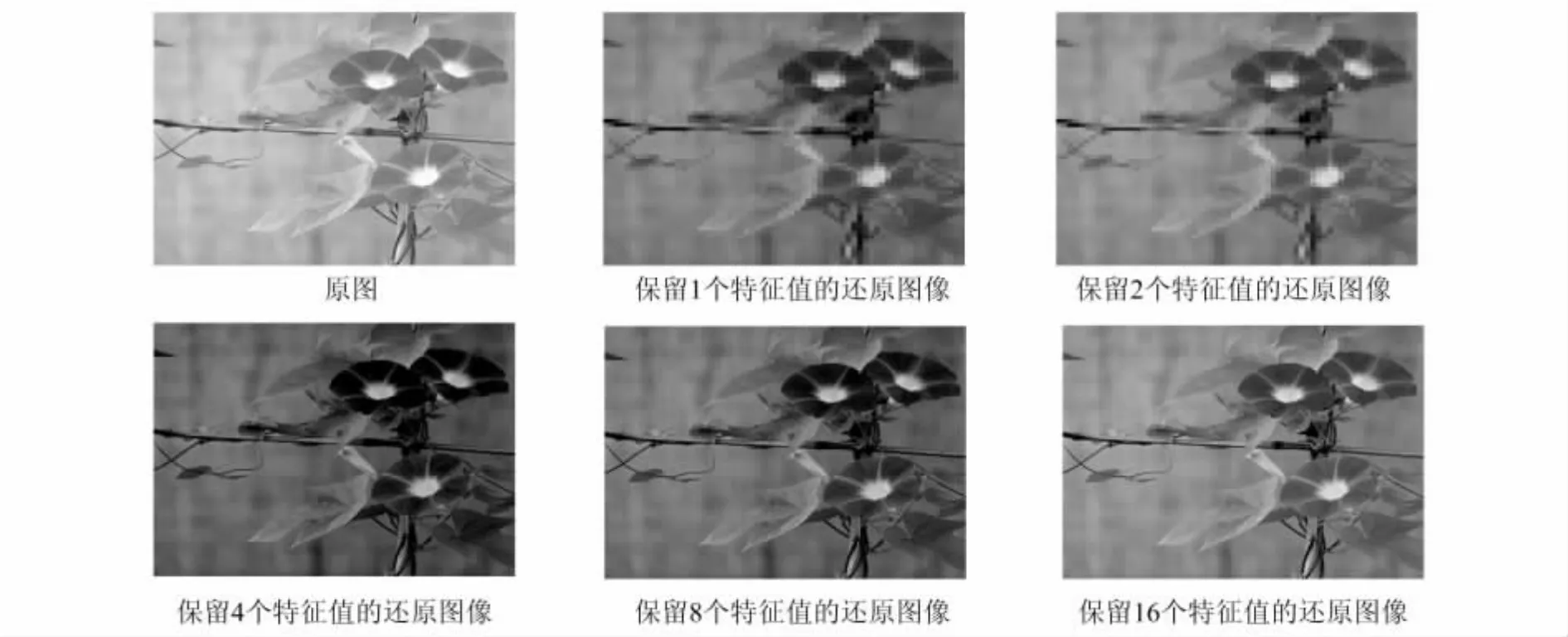
图6 牵牛花原图及保留特征值的重建图像Fig.6 The original image of morning glory and the reconstructed image of the eigenvalue
[1]Scott D C.The advantages of inverted operators in Rayleigh-Ritz approximations SIAMJ.Sci.Statist[J].Comput,1982,3:68-75.
[2]Bouras A,Fraysse V.A relaxation strategy for the Arnoldi method in eigenproblems,technical report TR/PA/00/16[R].France:CERFACS,Toul-ouse,2000.
[3]Morgan R B.Computing interior eigenvalues of large matrices[J].Linear Algebra Appl,1991,154:289-309.
[4]Morgan R B,Zeng M.Harmonic projection methods for large non-symmetric eigenvalue problems[J].Numer Linear Algebra Appl,1998,5:33-55.
[5]Bai J Z,Barret R,Day D,et al.Test matrix collection for non-Hermitian eigenvalue problems,Technical Report,Department of Mathematic,University of Kentucky,US,1995 [EB/OL].(2003-08-15),[2009-11-07].http//math.nist.gov/MatrixMarket/.
[6]赵荣椿,赵忠明,崔苏生.数字图像处理导论[M].西安:西北工业大学出版社,1999:66-70.
[7]Walker H F,Zhou L.A simpler GMRES[J].Numer Linear Algebra APPl,1994,1:57l-581.
[8]Morgan R B.Implicitiy restarted GMRES and Arnoldi methods for nonsymmetrics-tems of equations[J].SIAMJ Matrix Anal Appl,2000,21:1112-1135.
[9]Jia Z.The refined harmonic Arnoldi method and an implicitly restarted refined algorithm for computing interior eigenpairs of large matrices[J].Appl Numer Math,2002,42:489-512.
[10]Jia Z.The convergence of harmonic Ritz values,harmonic Ritz vectors and refined harmonic Ritz vectors[J].Math Comput,2005,74:1441-1456.
[11]王文峰.K-L变换的研究及其在图像压缩编码中的应用[D].沈阳:沈阳理工大学档案馆,2008.

