一种基于彼得罗夫伽辽金公式的三角形单元★

贾 程

(盐城工学院土木工程学院，江苏 盐城 224051)

0 引言

传统的等参有限单元模型满足变分一致性要求，能够较好的分析许多实际的问题，但是存在刚度矩阵过刚、对网格畸变敏感等问题。刚度矩阵过刚带来了自锁问题和计算精度下降问题，对于线性三角形单元尤其明显。对网格畸变敏感要求划分问题域的网格质量较高，如四边形单元要求其夹角尽量保持90°，这给前处理带来巨大的工作量。为了改善上述缺陷，学者们提出了许多方法:hybrid-Trefftz单元法[1]、无网格法[2]等，然而，这些方法还有局限性或不够完善的地方。

在实际应用时，工程师比较偏爱三角形单元。因为它们能够被自动的生成。本文使用非对称有限单元公式的概念，将线性三角形单元形函数和有限元无网格耦合三角形单元(FE-LSPIM TRI3单元)形函数分别作检验函数和试函数，构造出基于彼得罗夫伽辽金公式的US-FE-LSPIM TRI3三角形单元。

1 US-FE-LSPIM TRI3三角形单元公式

1.1 FE-LSPIM TRI3三角形单元的形函数

图1 支持域的定义

对于二维线弹性问题，采用三角形网格离散问题域，如图1所示。单元内任一点的位移可表示成:

其中，N′=[N1，N2，N3]是传统的线性三角形单元的形函数矩阵是由三个节点坐标决定的常数;ue={u1(x，y) u2(x，y) u3(x，y)}T是局部节点位移函数。在该节点处等于其位移值，即:ui(xi，yi)=ui，i=1，2，3。局部节点位移函数ui(x，y)利用Rajendran等[3]使用的最小二乘点插值无网格法(LSPIM)，由i点的支持域内的节点值拟合得到:

其中，φi=[φi1φi2φi3…φiN]，i=1，2，3，ui=[u1u2u3L uN]T。

其中，φi是LSPIM法的关于节点i的形函数矩阵;ui是节点i支持域内节点的位移参数向量;N为节点i支持域内的所有节点数。一个单元所有节点支持域的合集构成了一个单元的支持域Ω。

节点支持域和单元支持域的定义分别如图1所示。

将方程(2)代入式(1)得:

从方程(3)中，可以得到该单元的形函数矩阵，设单元支持域Ω内的节点数为M:

局部节点位移可以写成下列形式:

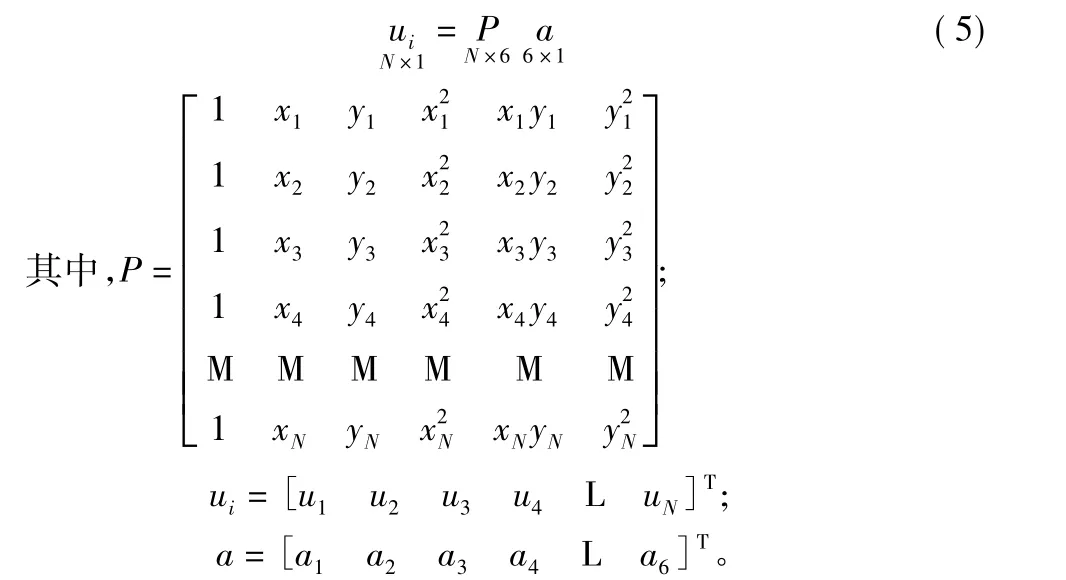
令该单元的第一个节点记为节点i。由于传统的最小二乘近似a=(PTP)－1PTui使得节点i的位移近似值不等于该点的位移值，即ui≠p(xi，yi)a，导致位移条件施加比较困难。故为了使节点i的位移近似值等于该点的位移值，利用方程(5)中的第一个方程解出a1，再从方程(5)其余的方程中消去a1，并由最小二乘法得:

其中，φi为局部节点位移函数的形函数;1为所有元素均为1的(N－1)行列向量;和的定义和文献[3]中相似，只是少了x2y和xy2项。利用式(4)进而可以求出单元的形函数矩阵ψ。

根据式(6)可以得出，在(xi，yi)点存在 ui(xi，yi)=ui，再根据式(4)可得FE-LSPIM TRI3三角形单元的形函数ψ具有Kronecker delta性质，能够像普通的有限元一样直接施加位移边界条件。

1.2 US-FE-LSPIM TRI3三角形单元公式

线弹性体系平衡状态的虚功方程为:

其中，δu为虚位移域;δε为响应的虚应变域;σ为真实应力。

由于ψ为线性三角形单元形函数和点插值无网格法形函数的复合函数，具有高阶的完备性，ψ插值的应力函数σ^比线性三角形单元的应力函数更加适合作试函数。对于检验函数，只要其满足边界条件和域内连续条件，故选择线性三角形单元形函数插值的虚位移域δ做检验函数。

将它们代入式(7)，并整理得:

2 检验算例

2.1 受弯矩作用的悬臂梁

如图2a)所示悬臂梁，在端部受常弯矩M=20C2作用，弯矩形式分布在右端，尺寸L=100，C=10，弹性模量 E=1.0 ×107，泊松比 μ =0.3，ρ=8 000 kg/m3，考虑平面应力状态。

图2 端部受弯矩的悬臂梁

采用2×6×2，2×10×2，4×16×2，6×20×2，8×28×2五种形式的三角形网格划分问题域，为了与四边形等参元比较，本问题也采用相应的2×6，2×10，4×16，6×20，8×28五种四边形网格划分。图2b)为2×6×2网格划分示例。A点的位移计算结果列于表1。

表1 A点的位移

从表1中可以看出，US-FE-LSPIM TRI3单元能够很好的重构常弯矩下的解，而传统的线性三节点三角形单元(T3)和四节点等参四边形单元(Q4)的结果不够精确。

2.2 Cook悬臂梁

本例为变截面的悬臂梁，在端部受一个分布剪力F=1/16作用，如图3a)所示。弹性模量E=1.0，泊松比μ=1/3。本问题采用2×2×2，4×4×2，8×8×2，16×16×2四种三角形网格划分形式。图3b)所示为4×4×2的形式。

图3 Cook悬臂梁

不同网格下A点的最小主应力列于表2。相比于T3和Q4单元，US-FE-LSPIM TRI3单元显示了最佳的结果。

表2 A点的最小主应力

3 结语

使用非对称有限单元法的概念，构造出基于彼得罗夫伽辽金公式的US-FE-LSPIM TRI3三角形单元。由于线性三角形单元形函数和FE-LSPIM TRI3单元形函数插值的位移函数能够满足域内位移连续性和完备性的要求，选择它们分别作为检验函数和试函数。数值算例显示，该US-FE-LSPIM TRI3三角形单元精度较高，优于传统的线性三角形单元和四边形等参元。

[1] FREITAS J A，BUSSAMRA F L S.Three-dimensional hybrid-Trefftz stress elements[J].International Journal for Numerical Methods in Engineering，2000，47(5):927-950.

[2] 张 雄，胡 炜，潘小飞，等.加权最小二乘无网格法[J].力学学报，2003，35(4):425-431.

[3] RAJENDRAN S，Zhang B R.A“FE-meshfree”QUAD4 element based on partition of unity[J].Computer Methods in Applied Mechanics and Engineering，2007，197(1-4):128-147.

[4] Timoshenko S P，Goodier J N.Theory of Elasticity[M].3rd edn.New York:McGraw-Hill，1934.

[5] 库 克，马尔库斯，普利沙.有限元分析的概念与应用[M].关正西，强洪夫，译.第4版.西安:西安交通大学出版社，2007.