n×n矩阵环的多项式恒等式
游松发,赵红艳
(湖北大学数学与计算机科学学院,湖北 武汉 430062)
1 预备知识
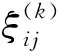
引理1[1]对于任何交换环C,Mn(C)≤φφn{Y}(符号“≤φ”表示φn{Y}的恒等式都是Mn(C)的恒等式).

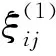
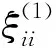
引理3[1]若φ是交换整环,则一定存在φ(ξ)(φξ)为φ[ξ]的分式域)的有限扩域F,使泛矩阵Yk在Mn(F)中可化为对角矩阵.
引理3的证明由procesi引理可直接得到证明.
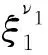
(1)
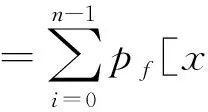
(2)
其中(2)式中yj的下标j取模n后的值.
2 主要结果及证明
定理4(i)若f[ξ1,…,ξn+1]中,在ξi=ξj(i≠j)时有f[ξ1,…,ξn+1]=0,则pf[x,y1,…,yn]是Mn(C)的恒等式.
(ii)若f[ξ1,…,ξn+1]中,除开ξ1=ξn+1外,在ξi=ξj(i≠j)时有f[ξ1,…,ξn+1]=0,则pf[x,y1,…,yn]x-xpf[x,y1,…,yn]是Mn(C)的恒等式,但pf[x,y]不是Mn(C)的恒等式.
(iii)若f[ξ1,…,ξn+1]满足(ii),且f[ξ1,…,ξn,ξ1]关于ξi是对称的,则qf[x,y1,…,yn]z-zqf[x,y1,…,yn]是Mn(C)的恒等式(也称之为Mn(C)的中心恒等式),但qf[x,y]不是Mn(C)的恒等式.
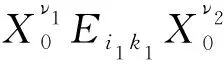
pf[X0,Ei1k1,Ei2k2,…,Einkn]=f[ξi1,…,ξin,ξkn]δk1i2δk2i3…δkn-1inEi1kn
(3)
其中δij=0(i≠j),δii=1(i=j).
由于f满足(i)的条件,又pf关于yi是线性的,因而对于对角矩阵X0和任意矩阵Yj,我们有
pf[X0,Y1,…,Yn]=0.
又由引理3,对于泛矩阵X,一定存在某代数扩域F,使X在Mn(F)中可以对角化,因此,当X,Y1,…,Yn是泛矩阵时,我们有
pf[X,Y1,…,Yn]=T-1pf[TXT-1,TY1T-1,…,TYnT-1]T=
T-1pf[X0,TY1T-1,…,TYnT-1]T=T-10T=0.
即pf[x,y1,…,yn]是φn{Y}的恒等式,再由引理1可知pf[x,y1,…,yn]是Mn(C)的恒等式.
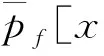
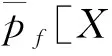
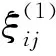
pf[Y1,E12,E23,…,E(n-1),n]=T-1f(ξ1,…,ξn,ξ1)E1nT≠0.
其中ξ1,…,ξn为泛矩阵Y1的n个不同的特征值(引理2),这样便证明了,若f[ξ]满足(ii)的条件,则pf[x,y]不是Mn(C)的恒等式.
(iii)对于(1,2,…,n)的任何置换(i1,i2,…,in),按(3)式一样的计算,把每一种置换的pf计算出来.y1,y2,…,yn若取楼梯Ei1i2,Ei2i3,…,Eini1,则pf[X0,Ei1i2,Ei2i3,…,Eini1]=f(ξi1,…,ξin,ξi1)Ei1i1,利用f[ξi1,…,ξin,ξi1]在ξi的对称性,得到qf[X0,Ei1i2,Ei2i3,…,Eini1]=f[ξi1,ξi2,…,ξin,ξi1]E
(4)
其中X0为对角阵,E为单位阵.
而y1,y2,…,yn对于矩阵单位{Eiνkν}中的其他任何一种非楼梯取法均有pf[X0,Ei1k1,Ei2k2,…,Einkn]=0,从而qf[X0,Ei1k1,Ei2k2,…,Einkn]=0,其中Ei1k1,…,Einkn是非楼梯,即
qf[X0,Ei1k1,Ei2k2,…,Einkn]=f[ξi1,ξi2,…,ξin,ξi1]δk1i2δk2i3…δkn-1inE
(5)
由(5)式可知,qf[X0,Ei1k1,Ei2k2,…,Einkn]为0或纯量阵,与任意矩阵是可换的,即∀Z,qf[X0,Ei1k1,…,Einkn]Z-Zqf[X0,Ei1k1,…,Einkn]=0.考察多项式qf[x,y]z-zqf[x,y],按(i)的证明过程,类似可证,对于对角矩阵X和任意矩阵Yi和Z,我们有qf[X,Y1,…,Yn]Z-Zqf[X,Y1,…,Yn]=0,按(i)同样的理由,可知qf[x,y]z-zqf[x,y]是Mn(C)的恒等式.
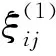
qf[Y1,E12,E23,…,En-1,n]=T-1f[ξ1,ξ2,…,ξn,ξ1]ET≠0.
其中ξ1,…,ξn为泛矩阵Y1的n个不同的特征值,这样便证明了f[ξ]若满足(iii)的条件,则qf[x,y]不是Mn(C)的恒等式.
由于0≢qf[x,y]∈Z(Mn(C))(Mn(C)的中心),所以qf[x,y]是Mn(C)的中心多项式,它是比Formanek中心多项式更为广泛的一类中心多项式[2],因此,也称qf[x,y]z-zqf[x,y]为Mn(C)的中心恒等式.
3 应用
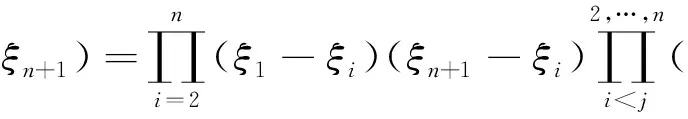
定理5qδ[x,y1,…,yn]不是Mn(C)的恒等式,若g(ξ1,…,ξn)关于ξi对称,则qgδ[x,y1,…,yn]-g(x)qδ[x,y1,…,yn]是Mn(C)的恒等式.其中,对x=α∈Mn(C),g(x)=g(a)=g(α1,…,αn),αi是α的特征根.
定理5的证明一方面,δ(ξ)满足定理4(iii)中f的条件,直接由定理4(iii)可知qδ[x,y1,…,yn]不是Mn(C)的恒等式.
另一方面,gδ也满足定理4(iii)中f的条件,考察对角阵X0=∑ξiEii,y1,y2,…,yn,若取楼梯Ei1i2,Ei2i3,…,Eini1,由(4)式(把gδ看作f),qgδ[X0,Ei1i2Ei2i3,…,Eini1]=g[ξ1,…,ξn]δ[ξ1,…,ξn,ξ1]E=g[ξ1,…,ξn]qδ[X0,Ei1i2,Ei2i3,…,Eini1].而y1,y2,…,yn对于矩阵单位{Eiνkν}中的其它任何一种非楼梯取法均有qgδ[X0,Ei1k1,Ei2k2,…,Einkn]=0,其中,Ei1k1,Ei2k2,…,Einkn是非楼梯.
仿照定理4,对任意矩阵Yi和泛对角矩阵X0,利用qgδ在yi的线性性,有
qgδ[X0,Y1,…,Yn]=g[ξ1,…,ξn]gδ[X0,Y1,…,Yn].
对泛矩阵X,则存在T,使TXT-1=X0,由于g(ξ1,…,ξn)关于X0的对角元ξi是对称的,即g(ξ1,…,ξn)关于X的特征根是对称的,因而可写g(ξ1,…,ξn)=g(X),我们有
0=qgδ[X0,T-1Y1T,…,T-1YnT]-g[ξ1,…,ξn]qδ[X0,T-1Y1T,…,T-1YnT],
0=T-1(qgδ[X,Y1,…,Yn]-g(X)qδ[X,Y1,…,Yn])T,
因此,qgδ[X,Y1,…,Yn]-g(X)qδ[X,Y1,…,Yn]=0,即qgδ[x,y1,…,yn]-g(x)qδ[x,y1,…,yn]是Mn(C)的恒等式.
在定理5中,(i)若选择g=σ0(ξ)=1,记qgδ=q0,我们有q0[x,y1,…,yn]=qδ[x,y1,…,yn],可知q0[x,y1,…,yn]不是Mn(C)的恒等式.
(ii)若g=σ1(ξ)=ξ1+…+ξn,记qgδ=q1,有q1[x,y1,…,yn]=qgδ[x,y1,…,yn]=g(x)qδ[x,y1,…,yn]=Tr(x)qδ[x,y1,…,yn],知q1[x,y1,…,yn]-Tr(x)qδ[x,y1,…,yn]是Mn(C)的一迹恒等式.
(iii)若g=σk(ξ)=∑ξi1ξi2…ξik,记qgδ=qk,有qk[x,y1,…,yn]=qgδ[x,y1,…,yn]=g(x)qδ[x,y1,…,yn]=σk(x)qδ[x,y1,…,yn],知,qk[x,y1,…,yn]-σk(x)qδ[x,y1,…,yn]是Mn(C)的一恒等式.
由于函数(-1)kσk(X)是矩阵X的特征多项式的系数,据(i)、(ii)、(iii)及Mn(C)的Cayley-Hamilton定理[1],有q0[x,y1,…,yn]xn-q1[x,y1,…,yn]xn-1+…+(-1)nqn[x,y1,…,yn]是Mn(C)的恒等式.
[1] Rowen L H.Polynomial identities in ring theory[M].New york:Academic Press,1980.
[2] Formanek.Central polynomials for matrix rings[J].J Algebra,1972(2):129-132.
[3] 游松发,郑玉美,胡动刚.欧拉图与矩阵环的多项式恒等式[J].数学进展,2003,32(4):425-428.
[4] Chang Q.A sort of polynomial identities ofMn(F) with charF>0[J].Chinese Ann Math Ser B,1988(9):161-166.
[5] Szigeti J,Tuza Z,Revesz G.Eulerian polynomial identities on matrix rings[J].J Algebra,1993,161:90-101.

