具可变扩散系数的椭圆-双曲方程组的全局适定性
李 健, 高文杰, 李建军, 王增辉
(1. 吉林农业大学 信息技术学院, 长春 130118; 2. 吉林大学 数学学院, 长春 130012; 3. 辽宁工程技术大学 理学院, 辽宁 阜新 123000)
0 引 言
考虑由Ward等[1]提出的一个偏微分方程组的自由边界问题, 该模型描述肿瘤球体对反肿瘤药物的反应. 本文考虑其可变扩散系数的问题:
(1)
其中:n,m,c,w和v为未知函数, 分别表示活细胞的密度(细胞个数/单位体积)、 死细胞的密度、 营养浓度、 药物浓度和肿瘤细胞的运动速度;Dc(r),Dw(r)表示依赖r的扩散系数, 并假设扩散系数具有正上、 下界; 函数kp,kd及f取Michaelis-Menten型, 即
这里A,B,cp,cd,σ,β和wc为正常数; 活细胞的增生率为kp, 自然死亡率为kd, 药物致死率为Kf; 常数K为药物导致细胞死亡的最大值;ω为药物有效性的一个度量.
假设球体由活细胞和死细胞组成, 反肿瘤药物及营养物的分子相对与肿瘤细胞非常小. 记VL和VD分别为单个活细胞和死细胞的体积, 则
VLn+VDm=1.
(2)
定义r0=(3VL/4π)1/3为单个活细胞的半径.
在自由边界r=R(t)上, 取边界条件为
(3)
其中:c0是外部营养浓度(假设固定);w0(t)是非负函数;R(t)是肿瘤的球半径.
施加下面的初始条件:
R(0)=R0,n(r,0)=n0(r),c(r,0),w(r,0),
(4)
并假设:

(5)
其中:w0为正常数;c(r,0),w(r,0)分别为初始的营养浓度和药物浓度. 本文假设:w0(t)∈C[0,+∞),n0(r)∈C1[0,R(0)].
用VL,VD分别乘式(1)的前两个方程, 再利用式(2), 得
该方程可以代替式(1)的第二个方程.
做非量纲变换:
开始时的半径R(0)可以认为远比r0大. 经过上面的变换, 方程组可以写成如下形式:
(6)
其中:

1 全局存在唯一性
引理1[4]设V(ρ,t)是定义在[0,1]×[0,T]上并满足V(0,t)=V(1,t)=0(0≤t≤T)的有界函数,f(ρ,t,n)是定义在(ρ,t,n)∈[0,1]×[0,T]×R上的连续函数, 并且关于变量(ρ,n)连续可微. 考虑如下问题:
(12)
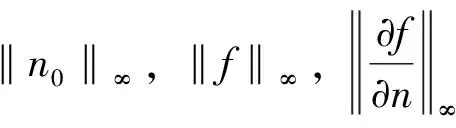
‖n‖∞≤‖n0‖∞+T‖f‖∞.
而且如果n0∈C1[0,1], 则弱解实际上是古典解, 并且下面的估计成立:

由式(11), 得
(13)
因此v(0.t)=0, 并且v(ρ,t)关于变量ρ可微.
记M=max{b(c,w)n: 0≤n≤1, 0≤c≤1, 0≤w≤w0(t)}. 对给定的T, 引入度量空间(XT,d):XT包含满足如下假设条件的向量函数(R,n,c,w)=(R(t),n(ρ,t),c(ρ,t),w(ρ,y))(0≤ρ≤1, 0≤t≤T):
(H2)n(ρ,t)∈C([0,1]×[0,T]),n(ρ,0)=n0(ρ), 0≤n≤1;
(H3)c(ρ,t)∈C([0,1]×[0,T]),c(1,t)=1, 0≤c≤1;
(H4)w(ρ,t)∈C([0,1]×[0,T]),w(1,t)=w0(t), 0≤w≤w0(t).
其中
d((R1,n1,c1,w1),(R2,n2,c2,w2))=‖R1-R2‖∞+‖n1-n2‖∞+‖c1-c2‖∞+‖w1-w2‖∞.
易证(XT,d)是个完备的度量空间.

并分别考虑如下4个问题:
显然问题(17)有唯一的解
(18)
由b(c,w)n≤M, 得


(19)
又由0≤n≤1, 式(18),(19)及椭圆方程的Lp估计, 得
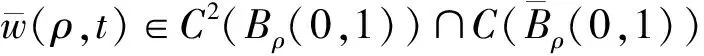

对任意给定的t1,t2∈[0,T], 有
利用Lp估计, 得
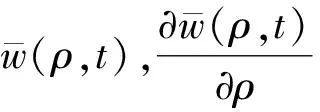
综上, 映射F是当T充分小时把XT映射到其本身的. 下面证明当T更小时,F是压缩映射.
令(Ri(ρ,t),ni(ρ,t),ci(ρ,t),wi(ρ,t))∈XT(i=1,2), 则
直接计算, 得
由式(18), 得
(20)


由线性方程的最大模估计知
同理可得
(22)

又由引理1及n0∈C1, 易得
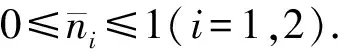
由式(20)~(23), 可得
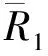
因此, 如果T充分小, 使得TC(T)<1, 则F是从XT到其本身的压缩映射.
由Banach不动点定理知, 如果T充分小, 则F在XT中有唯一的不动点(R,n,c,w). 又由F的定义知, 不动点(R,n,c,w)是问题(7)~(11)在0≤t≤T上的唯一解. 类似于文献[11]的方法, 可得如下局部存在定理:
定理1假设w0(t)>0是在[0,+∞)上的一个连续有界函数, 如果T充分小, 则问题(7)~(11)有唯一解(w(r,t),c(r,t),n(r,t),v(r,t),R(t))((ρ,t)∈[0,1]×[0,T]), 使得w(r,t),c(r,t)∈C2(0,R(t))∩C[0,R(t)](t∈[0,T]),R(t)∈C1[0,T],n(r,t)∈C1([0,R(t)]×[0,T]), 并且有
为证明问题(7)~(11)解的全局存在性, 首先应证明下面的引理.
引理2如果问题(7)~(11)的解(R,n,c,w)在0≤t 1) 0≤n(ρ,t)≤1, 0≤ρ≤1, 0≤t 3)c(ρ,t)∈C(0,1),w(ρ,t)∈C(0,1),t为参数; 4)R0e-Mt/3≤R(t)≤R0eMt/3,M=maxb(n,c,w); 5)n(ρ,t)∈C1(0,1). 证明: 由文献[10]中定理2.2可得断言1). 由椭圆方程的极值原理知断言2)成立. 由断言1)和2)可得b(n,c,w)≤M. 由式(10),(13), 易得断言3). 利用椭圆方程的Lp估计知 定理2满足定理1中条件的问题(7)~(11)的解全局存在. 证明: 令0≤t [1] Ward J P, King J R. Mathematical Modelling of Drug Transport in Tumour Multicell Spheroids and Monolayer Cultures [J]. Math Biosci, 2003, 181(2): 177-207. [2] Bueno H, Ercole G, Zumpano A. Asymptotic Behaviour of Quasi-stationary Solutions of a Nonlinear Problem Modelling the Growth of Tumours [J]. Nonlinearity, 2005, 18(4): 1629-1642. [3] TAO You-shan, CHEN Miao-jun. An Elliptic-Hyperbolic Free Boundary Problem Modelling Cancer Therapy [J]. Nonlinearity, 2006, 19(2): 419-440. [4] CUI Shang-bin, WEI Xue-mei. Global Existence for a Parabolic-Hyperbolic Free Boundary Problem Modeling Tumor Growth [J]. Acta Math Appl Sin: Eng Ser, 2005, 21(4): 597-614. [5] HOU Xiu-mei. Asymptotic Behavior of Solutions of a Free Boundary Problem Modeling Multi-layer Tumor Growth in Presence of Inhibitor [J]. Acta Math Appl Sin: Eng Ser, 2011, 27(8): 1621-1636. [6] XU Shi-he. Qualitative Analysis of a Delayed Free Boundary Problem for Tumor Growth under the Effect of Inhibitors [J]. Nonlinear Analysis: Theory, Methods and Applications, 2011, 74: 3295-3304. [7] HOU Xiu-mei, CUI Shang-bin. Stability of Stationary Solutions for a Multi-dimensional Free Boundary Problem Modeling Tumor Growth [J]. Adv Math Sci Appl, 2009, 19: 449-464. [8] CUI Shang-bin, Escher J. Bifurcation Analysis of an Elliptic Free Boundary Problem Modelling the Growth of Avascular Tumors [J]. SIAM J Math Anal, 2007, 39: 210-235. [9] Ladyzhenskaya O A, Ural’tseva N N. Linear and Quasilinear Elliptic Equations [M]. New York: Academic Press, 1968. [10] Friedman A, Tao Y. Analysis of a Model of a Virus That Replicates Selectively in Tumor Cells [J]. J Math Biol, 2003, 47(5): 391-423. [11] LI Jian, GAO Wen-jie, LIU Lin-lin. Global Solvability of Nonlinear Diffusion Equations with Forcing at the Boundary [J]. Journal of Jilin University: Science Edition, 2008, 46(5): 801-808. (李健, 高文杰, 刘琳琳. 边界受控的非线性扩散方程的整体可解性 [J]. 吉林大学学报: 理学板, 2008, 46(5): 801-808.)