环面链环的多项式

陶志雄

(浙江科技学院 理学院，杭州 310023)

环面链环的多项式

陶志雄

(浙江科技学院 理学院，杭州 310023)

纽结或者链环多项式的计算通常牵涉递归问题。研究利用二次方程的韦达定理来解决这些递归问题，从而得到环面链环T(2,m)的Conway多项式和Jones多项式的表达式。

Conway多项式；Jones多项式；环面链环

环面纽结T(m,n)(m,n互素)的Jones多项式早已由Jones本人利用Hecke代数及辫子群理论等给出了公式和证明[1]。公式的给出过程非常艰难和复杂，目前没有几何化的证明[2]。据笔者的调查，没有任何环面链环的Jones多项式表达式的研究结果。本研究主要关注环面纽结T(2,m)的多项式表示。约定环面链环或者环面纽结T(2,m)总表示其有|m|个与m同号的交叉，利用二次方程的韦达定理等方法给出环面纽结T(2,m)的Conway多项式和Jones多项式的表达式，即有：

定理1若T(2,m),m≠0是两个分支方向相同的环面链环，则

这里[x]表示取整数，sign(x)表示x的符号。第二个公式也适合环面纽结的情形。

定理2若T(2,m)是2个分支的方向相同的环面链环，则其Jones多项式为：

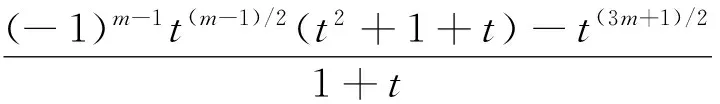
注：如果2个分支的方向相反，那么可以参考文献[3]和[4]来修改和利用定理2的结果。

1 基本知识

2)若3个纽结或链环L+,L-,L0仅在一处不同，而且不同处如图1所示，

图1 链环(纽结)L+,L-,L0Fig.1 Links(knots)L+,L-and L0

则2个多项式分别满足：

那么，这2个多项式都是纽结与链环不变量，分别称为Conway多项式和Jones多项式。

命题[1-2]环面纽结T(p,q)(p,q互素)的Jones多项式为:

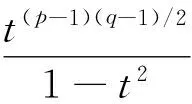
2 定理1的证明

(1)

若设α+β=z,αβ=-1，可知道α,β满足方程：x2-zx-1=0，解方程得

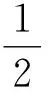
于是原方程(1)可改写为:

(2)

但原方程(1)也可以改写为:

(3)

(2)×β-(3)×α得

这样

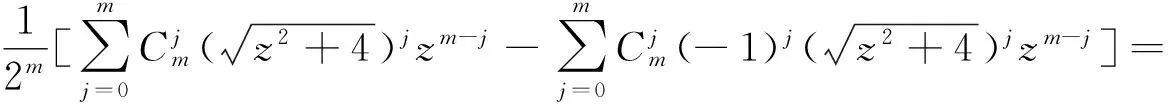
利用上面的证明，可以得到一个环面链环的Conway多项式的赋值公式,即

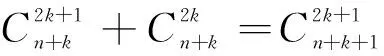
3 定理2的证明

首先计算m≥0时的V(T(2,m);t)。

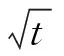
t-1V(T(2,m);t)-tV(T(2,m-2);t)=(t1/2-t-1/2)V(T(2,m-1);t)，
V(T(2,m);t)=(t1/2-t-1/2)tV(T(2,m-1);t)+t2V(T(2,m-2);t)

设α+β=(t1/2-t-1/2)t,αβ=-t2，可知道α,β满足方程：

x2-(t1/2-t-1/2)tx-t2=0，

解方程得

α=t3/2,β=-t1/2。

于是原方程可改写为

V(T(2,m);t)-αV(T(2,m-1);t)=β(V(T(2,m-1);t)-αV(T(2,m-2);t))=

βm-2(V(T(2,2);t)-αV(T(2,1));t)，

(4)

但原方程也可以改写为：

V(T(2,m);t)-βV(T(2,m-1);t)=α(V(T(2,m-1);t)-βV(T(2,m-2));t)=

αm-2(V(T(2,2))-βV(T(2,1)))，

(5)

(4)×β-(5)×α得

V(T(2,m);t)(β-α)=βm-1(V(T(2,2);t)-αV(T(2,1));t)-αm-1(V(T(2,2);t)-βV(T(2,1));t)=

βm-1(-t5/2-t1/2-t3/2)-αm-1(-t5/2-t1/2+t1/2)=

(-1)mtm/2(1+t+t2)+t3m/2+1。

这样

显然上述等式适合任何m≥0的整数。对于m<0，由于T(2,m)的镜面像是T(2,-m)，且V(T(2,m);t)=V(T(2,-m);t-1)，

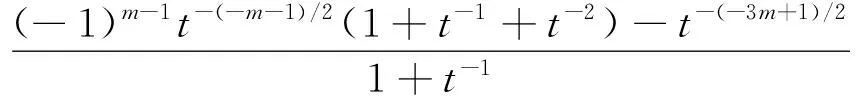
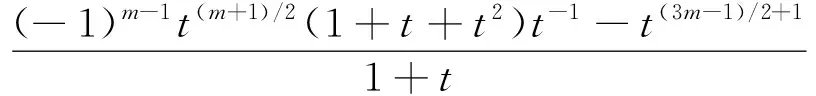
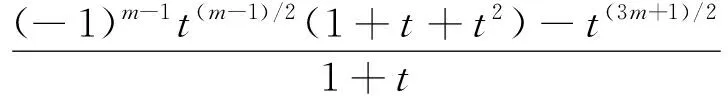
尤其是：

使用常规的递推方法及环面纽结情形的Jones多项式，也可以得出上述环面链环的Jones多项式。

由于V(T(2,1))=1，V(T(2,2))=-t5/2-t1/2，当m>2时，

t-1V(T(2,2n))-tV(T(2,2n-2))=(t1/2-t-1/2)V(T(2,2n-1))，
V(T(2,2n))=t2V(T(2,2n-2))+t(t1/2-t-1/2)V(T(2,2n-1))
……
V(T(2,2))=t2V(T(2,0))+t(t1/2-t-1/2)V(T(2,1))

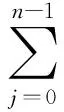
[1] Jones V F R. Hecke algebra representations of braid groups and link polynomials[J]. Annals of Mathematics,1987,126(2)：335-388.

[2] Adams C C. The knot book: An Elementary Introduction to the Mathematical Theory of Knots[M]. Providence, Rhode Island: American Mathematical Society,2004.

[3] Lickorish W B R, Millett K C. The reversing result for the Jones polynomial[J]. Pacific Journal of Mathematics,1986,124(1):173-176.

[4] Murasugi K. Knot Theory and Its Applications[M]. Boston, Basel, Berlin: Birkhäuser, 1996.

[5] 陶志雄. 颠倒分支定向的链环的Jones多项式[J]. 浙江科技学院学报，2011，23(6):443-444.

[6] Kauffman L H. On knots(Annals of Mathematics Studies 115)[M]. Princeton: Princeton University Press,1987.

Polynomialsofatoruslink

TAO Zhixiong

(School of Sciences, Zhejiang University of Science and Technology, Hangzhou 310023, China)

Knot or link polynomial calculations often involve recursion problems. This paper solves these problems by using Vieta’s formulas for the quadratic equation. From this way, it gives expressions of the Conway polynomial and the Jones polynomial of a torus linkT(2,m).

Conway polynomial; Jones polynomial; torus link

O189.24

A

1671-8798(2013)06-0405-04

10.3969/j.issn.1671-8798.2013.06.001

2013-06-01

浙江省自然科学基金资助项目(LY12A01025);浙江省自然科学基金青年基金资助项目(LQ13A010018)

陶志雄(1961— )，男，浙江省绍兴人，副教授，博士，主要从事几何拓扑学研究及大学数学教学。