F2上二阶线性半群到域K上二阶线性半群的同态
朱 捷, 刘 莹, 杜广环
(黑龙江科技大学 理学院, 哈尔滨 150022)
F2上二阶线性半群到域K上二阶线性半群的同态
朱捷,刘莹,杜广环
(黑龙江科技大学 理学院, 哈尔滨 150022)
为探讨二阶线性半群间的同态问题,在引进标准型、延断型、平凡型概念的基础上,通过矩阵计算与群的定义关系,描述了二元域F2上的线性半群M2(F2)到任意域K上的线性半群M2(K)的同态形式。进而为描绘F2上的线性半群Mn(F2)到任意域K上的线性半群Mm(K)(n≥m)的同态形式,奠定了坚实的基础。
域; 线性群; 线性半群; 延断; 同态
0 引 言
线性半群同态近年来引起许多学者关注,已成为矩阵代数中重要的研究课题[1-7]。笔者描绘了F2上的n阶线性群到域K上的m阶线性群(n=m=2,n=m≥3,n>m)的同态形式[1-3],从而完全描述了二元域F2上一般线性群的同态形式。但关于矩阵半群同态的描绘并不多[4-7],因此,笔者使用矩阵计算与群的定义关系,结合文献[1-3]中已有的一般线性群结果,通过引入标准型、延断型、平凡型、特殊型的概念,描述M2(F2)到M2(K)的线性半群同态形式(仅保持乘法未必保单位矩阵的映射)。
1 基础知识
设K为域,n∈Z+,SLn(K)、GLn(K)、Mn(K)分别表示K上的n阶特殊线性群、一般线性群、线性半群。以F2表示仅含两个元素的域。Tij(λ)(i≠j,λ∈K*)为将n级单位矩阵中(i,j)位置的元素易之以λ所得到的矩阵,其Tij(1)简写为Tij。对于X∈Mn(K),记iPX=P-1XP,其中P∈GLn(K)。
由文献[1-3,8]可知,下述映射φ是M2(F2)到M2(K)的半群同态(仅保持乘法,未必保单位矩阵)(n≥m)。
(Ⅰ)标准型
(1)φ(X)=PXτP-1,∀X∈Mn(F2),其中P∈GLm(K),τ:F2→K为嵌入。
(2)φ(X)=P(X*τ)′P-1,∀X∈Mn(F2),其中P∈GLm(K),X*为X的伴随矩阵,τ同(1)。
(Ⅱ)延断型
设φ1:GLn(F2)→GLm(K)为非平凡同态,则称下列映射φ为φ1在Mn(F2)到Mm(K)的延断。
(Ⅲ)平凡型
设r,s∈{0,1,…,m},r≤s,P∈GLm(K),置
其中,对于任意n,m∈Z+,任意域K,称其为平凡同态,并以In,s,r表之。
(Ⅴ)特殊型
设ChK≠2,φ:M2(F2)→M2(K),
易证,φ为同态。
2 主要结果
定理1[1]设K为域,
(1)B∈GL2(K),B2=I2,则下列映射是GL2(F2)到GL2(K)的同态
φ(X1)=B,φ(X2)=I2,
其中X1,X2分别为GL2(F2)的任意2阶元与3阶元。
(2)若ChK≠2,b,c∈K,bc=3/4,则下述映射φ是GL2(F2)到GL2(K)的同态,且具有下述形式:
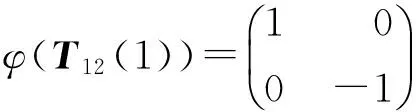
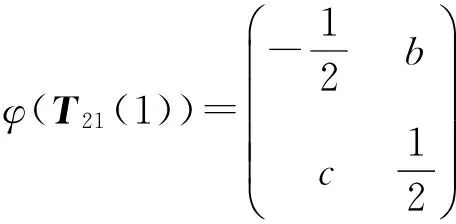
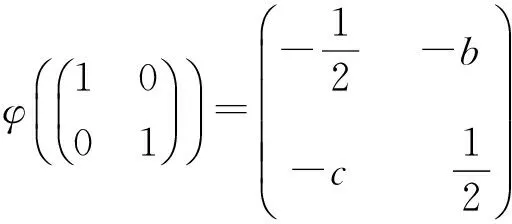
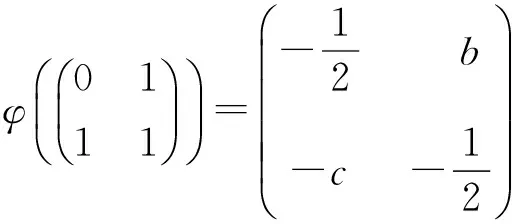
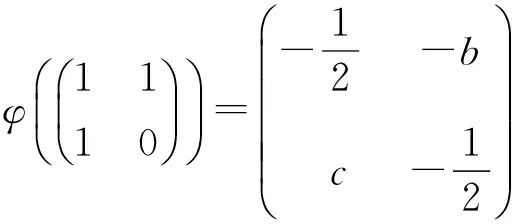
φ(I2)=I2。
定理2[1]设K为域,φ:GL2(F2)→GL2(K)为群同态,则φ为非平凡的当且仅当φ为下述三种形式之一:
(1)∃P∈GL2(K),嵌入τ:F2→K,使
φ(X)=PXτP-1, ∀X∈GL2(F2)。
(2)存在GL2(K)的2阶元B,使
φ(X1)=B,φ(X2)=I2,
其中X1,X2分别为GL2(F2)的任意2阶元与3阶元。
(3)ChK≠2,∃P∈GL2(K),使iPφ适合定理1中φ确定的形式。
定理3设φ:M2(F2)→M2(K)为半群同态,则
(1)φ=I2,2,2,I2,2,1,I2,2,0,I2,1,1,I2,1,0,I2,0,0。
(2)当ChK=2时,φ为标准型或标准型延断,或者为下述φ1的延断:
φ1(X)=PT12(1)P-1,φ1(Y)=I2。
其中X∈GL2(F2)为任意2阶元,Y=I2或为3阶元,P∈GL2(K)。
(3)当ChK≠2时,φ为下述φ1,φ2,φ3之一的延断,其中
φ1(X)=-I2,φ1(Y)=I2,
φ2(X)=P[1,-1]P-1,φ2(Y)=I2,
φ3(X)=P[-1,0]P-1,φ3(Y)=P[1,0]P-1。
其中,X∈GL2(F2)为任意2阶元,Y∈GL2(F2)为任意3阶元。
(4)φ为特殊型。
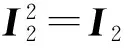
iPφ(I2)=[1,0]。
(1)
当(4)成立时,φ诱导出GL2(F2)→GL2(K)的解同态。由定理2,有下述4种形式:
(i)φ:X→I2,∀X∈GL2(F2)。
(ii)存在P∈GL2(K),嵌入τ:F2→K,使
φ(X)=P-1XτP-1,∀X∈GL2(F2)。
(iii)存在P∈GL2(K),使
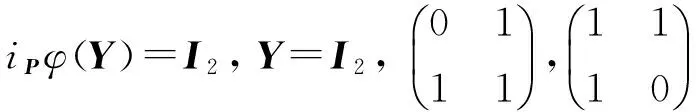
(iv)ChK≠2,存在P∈GL2(K),使得
iPφ(T12(1))=[1,-1],
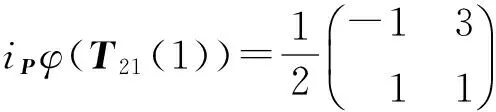
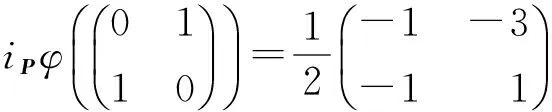
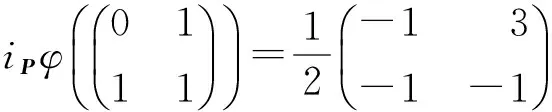
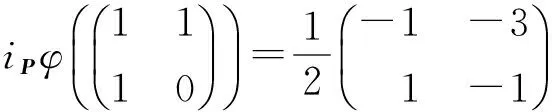
当X≠O时,有T1,T2∈GL2(F2),使X=T1E11T2,推出iPφ(X)=iPφ(E11)。
从而φ=I2,2,2,I2,2,1或I2,2,0。
如果(ii)成立,即iPφ(X)=Xτ,∀X∈GL2(F2)。经
(2)
推出
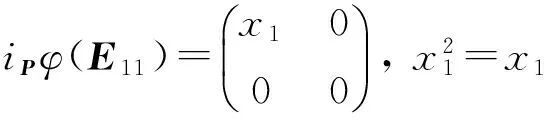
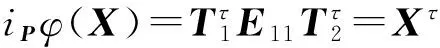
从而φ为标准型。
若iPφ(E11)=O,不难指出,φ为标准型的延断。
如果(iii)成立,当ChK=2时,对于任意的二阶元X,有iPφ(X)=T12(1)。经式(2)计算,可知
iPφ(X)=O, ∀X∈M2(F2)GL2(F2)。
即φ为延断。
当ChK≠2时,若iPφ(T12(1))=[1,-1],经式(2)可知iPφ(E11)=aE11,a=0或1。
对于a=0,易见φ为延断。对于a=1,不难指出iPφ为特殊型。
若iPφ(T12(1))=-I2,即φ(T12(1))=-I2,经式(2)推出φ(E11)=O,易见φ为延断。
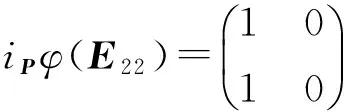
当式(1)成立时,经T12∈GL2(F2)为二阶元,可知存在iPφT12(1)=[1,0]或[-1,0],由此不难指出
iPφ(X)=[1,0], ∀X∈GL2(F2)。
(3)
或者当ChK≠2时,
iPφ(X)=[-1,0],iPφ(Y)=[1,0]。
(4)
其中X∈GL2(F2)为任意2阶元,Y=I2或为3阶元。
当式(3)发生时,经式(2)可推出iPφ(E11)=E11或O,因而φ=I2,1,1或I2,1,0。
当式(4)发生时,经式(2)不难指出φ为延断。证毕。
[1]朱捷, 张晓光, 母丽华.F2上线性群GL2(F2)到域K上线性群GL2(K)的同态[J]. 黑龙科技学院学报, 2004, 14(4): 255-256.
[2]朱捷. 二源域上一般线性群到任意域上线性群的同态[J]. 吉林大学学报: 理学版, 2005, 43(3): 268-274.
[3]朱捷, 母丽华, 王佳秋.F2上的n阶线性群到域K的m阶线性群的同态[J]. 哈尔滨商业大学学报: 自然科学版, 2005, 21(3): 340-341.
[4]朱用文, 郭爱丽. 带数乘的矩阵半群[J]. 数学学报: 中文版, 2010, 53(6): 1181-1186.
[5]左落粟, 朱用文. 矩阵单逆半群[J]. 吉林大学学报: 理学版, 2010, 48(5): 733-736.
[6]朱用文, 陈大亮. 交换矩阵半群的可约性[J]. 数学学报: 中文版, 2010, 53(5): 905-910.
[7]朱用文. 正则矩阵半群[J]. 数学进展, 2009, 38(1): 75-78.
[8]华罗庚, 万哲先. 典型群[M]. 上海: 上海科学技术出版社, 1963.
(编辑王冬)
Homomorphism ofF2’s second-order linear semigroup to fieldK’s second-order linear semigroup
ZHUJie,LIUYing,DUGuanghuan
(School of Sciences, Heilongjiang University of Science & Technology, Harbin 150022, China)
Aimed at discussing the problem of homomorphism of second order linear semigroup, this paper draws on the concept of the standard type, extension-cut type, ordinary type, the methods of the matrix calculation, and defining relation of group to describe all homomorphism of the general linear semigroupM2(F2) on theF2to the general linear semigroupMm(K) on the fieldK. The discussion serves as a basis for the homomorphism form of the linear semigroupM2(F2) on theF2to the linear semigroupM2(K)(n≥m) on the any fieldKas well.
field; linear group; linear semigroup; extension-cut; homomorphism
2013-04-22
黑龙江省教育厅科学技术研究项目(12511483)
朱捷(1964-),女,黑龙江省哈尔滨人,教授,博士,研究方向:典型群,E-mail:zhujie6411@163.com。
10.3969/j.issn.1671-0118.2013.03.021
O152.3
1671-0118(2013)03-0311-03
A
——如何培养学生的创新思维

