基于插入-分段的无等待流水作业调度复合启发式算法
李亚志 朱 夏
(东南大学计算机科学与工程学院,南京 211189)
(东南大学计算机网络与信息集成教育部重点实验室,南京 211189)
无等待流水作业调度是实际生产调度环境中一个重要的有约束组合优化问题,可描述为:n个任务在m台机器上按给定加工时间,顺序进行加工,且任务在加工过程中不能被中断.常见的优化目标有最小化最大完工时间[1-2]、总延迟[3]和总完工时间[4-6]等.其中,最小化总完工时间是实际应用中的重要指标,可促进资源的稳定有效利用、任务的快速周转以及制品库存的最小化.该问题在m≥2时为NP-难问题[4].
目前,通常采用元启发式和启发式算法求解该问题.元启发式算法包括声搜索算法[6]、离散粒子群算法[7]、基于可变邻域搜索的混合遗传算法[8]等.启发式算法可分为构造启发式算法和复合启发式算法.Rajendran等[9]提出了2种基于任务插入的构造启发式算法.Bertolissi[10]提出了1种基于比较的构造启发式算法.Aldowaisan等[4]基于置换策略提出了4种复合启发式算法.Framinan等[5]提出了1种复合启发式算法(FNM).FNM算法是目前用于求解最小化总完工时间的无等待流水作业调度问题的最新复合启发式算法.
元启发式算法随着任务数n的增加,其运行时间会越来越长,难以适用于实时性要求高的大规模无等待流水作业调度问题.在启发式算法中,邻域结构的设计是提高算法性能的关键.鉴于此,本文构造了一个基于插入-分段的邻域结构,提出了一种基于插入-分段的复合启发式算法(ISCH),同时采用文献[2]提出的目标增量法来评价新构造的解,降低算法运行时间.
1 问题描述
最小化总完工时间的无等待流水作业调度问题可描述为,从零时刻开始,n个具有相同工艺路线的任务按照给定加工次序,在m台机器上顺序加工,且满足如下假设:① 每台机器1次只能加工1个任务;② 每个任务不能同时在多台机器上加工;③ 工序准备时间包含在加工时间内,与顺序无关;④ 任务一旦开始加工便不允许中断;⑤ 任务未到达时允许机器闲置.
设任务j在机器k上的加工时间为tj,k.Tj为任务j在m台机器上的加工时间之和.在解π中引入开始虚任务j0,规定j0在每台机器上的加工时间为0.得到n+1个任务的一个解π={π[0],π[1],π[2],…,π[n]},且π[0]≡j0.令di,j为解π的相邻任务i和j在第1台机器上的开工时间间隔 (即二者的距离).则解π的目标函数值是总完工时间,即
(1)
式中,
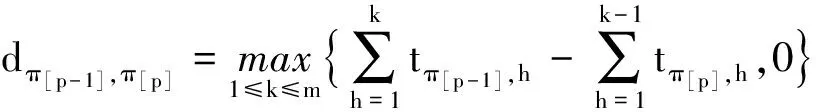
(2)
根据式(2)可以求出由n+1个任务组成的任意2个不同任务之间的距离矩阵.同时规定,对任务j,dj,j=∞(1≤j≤n);虚任务j0是任意解π的起始任务,它不会成为任何其他任务的后继,故dj,j0=∞(1≤j≤n).由于求解di,j的时间复杂度为O(m),因此,求解距离矩阵的时间复杂度为O(mn2).
基于已知的距离矩阵,求解F(π)的时间复杂度为O(n),而求最小化总完工时间的无等待流水作业调度问题的最优解就是在全体可行解空间Π中找到一个解π*,使得
F(π*)≤F(π) ∀π∈Π
(3)
2 基本性质
启发式算法的基本思想是搜索.常用的基本邻域结构操作主要有3种:插入、移位和对换.根据无等待流水作业调度的解中任务距离的独立性和式(1),应用目标增量法[2],对这3种基本操作的性质进行分析.
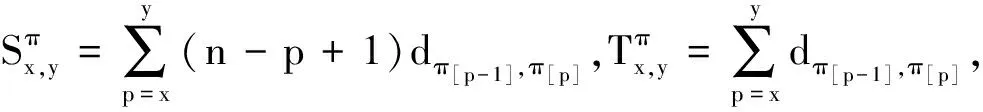
定理1若将任务j插入到解π中的位置p(0≤p≤n)之后,则插入目标增量ΔI为
(4)
式中,
π′={π[0],…,π[p],j,π[p+2],…,π[n+1]}
证明解π′的总完工时间为
(5)
式中,n′=n+1为解π′的任务数.
式(5)减去式(1),得
ΔI=F(π′)-F(π)=
证毕.
定理2若将解π中的任务π[p]从位置p移到位置q(1≤p,q≤n),则移位目标增量ΔM为
(6)
定理3若将解π中分别位于位置p和q的任务π[p]和π[q](1≤p (7) 定理2和定理3的证明过程类似于定理1. 使用由3种基本操作构成的邻域结构进行搜索,可使目标增量的时间复杂度降为O(1).因此,应用基本操作的目标增量方法可以大大减少算法的运行时间. 本文针对最小化完工时间的无等待流水作业调度问题提出ISCH算法.其主要思想为:首先,根据问题特点构造初始解;然后,从初始解中依次选取一个未处理任务,在当前解中找到任务最佳插入位置,并采用基于插入-分段的优化方法优化新解;迭代上述过程,直至初始解为空;最后,应用迭代序对对换算法是(IBSC)进一步优化当前解,得到问题的最终解. 根据定理1,当一个新任务插入到当前解的所有可能位置时,可求出插入到这些位置的目标函数增量;选取引起目标函数增量最小的位置作为最佳插入位置,将新任务插入到这个位置产生新解,而无需产生整个邻域的解.由此,便可构造基本邻域结构的新任务最佳位置插入算法(JBIP).该算法的具体描述如下: 1 Temp=∞,Pos=-1; 2 Forp=0 ton 根据定理1计算当任务j插入到解π的位置p之后的增量ΔI; 如果Temp>ΔI,则Temp=ΔI,Pos=p; 3 如果Pos≠-1,则将新任务j插入到解π的最佳插入位置Pos,得到新的解π; 4 返回π. JBIP算法的时间开销主要在第2步,其时间复杂度均为O(n),因此JBIP算法的时间复杂度为O(n). 类似地,可根据定理2和定理3分别构造出时间复杂度均为O(n)的任务最佳移位算法(JBMP)和任务对最佳对换算法(JBSP). 初始解对最终解有重要影响.本文提出了一种将所有任务按照Tj非降序排序的初始解生成方法(ISG),若存在加工时间相同的任务,则根据式(2)优先排序距离当前已排序解中尾任务最近的任务. 应用JBIP算法可得任务j的最佳插入位置,同时将解π分段成左、右2个子解πL={π[1],…,π[Pos],j}和πR={j,π[Pos+1],…,π[k]}.由于2个子解任务间的内在原有关联关系被改变,因此可采用移位局部优化算法(MLO),对子解σ进行优化.MLO算法的具体描述如下: 1 令n为子解σ的长度; 2 Forp=1 ton 如果σ[p]≠j,则 调用最佳移位算法JBMP,寻找σ[p]在σ中的最佳移位位置并在σ中进行移位操作; 3 返回σ. MLO算法的时间开销主要在第2步,其时间复杂度为O(n2),故该算法的时间复杂度为O(n2). 构造解算法(SGA)用于构造生成新的解.本文采用NEH算法思想[11],设计SGA算法.其基本思想为:从初始解Q中选取1个未排序任务插入到当前解πC的最佳位置,采用MLO算法对左、右2个子解πLC和πRC分别进行移位局部优化;重复上述过程直到Q为空. SGA算法的具体描述如下: 1πC=Φ; 2 Forp=1 ton 调用最佳位置插入算法JBIP将Q[p]插入πC; 将πC中Q[p]两侧的子解(含Q[p])置为πLC和πRC; 如果p≥3,则 调用移位局部优化算法MLO(πLC,Q[p]); 调用移位局部优化算法MLO(πRC,Q[p]); 3 返回πC. SGA算法的时间开销主要在第2步,其最坏时间复杂度为O(n3),故SGA算法的时间复杂度为O(n3). 针对SGA算法生成的解,可应用序对对换算法进行优化[5].根据对换方向和后续操作起点的不同,对换可分为FSC,BSC,FSR和BSR四种.不同对换算法对相同解的优化效果不相同,其中BSC算法对解的优化效果最好[2].另外,实验发现,在一定的迭代次数内,BSC算法能进一步优化解.因此,本文采用迭代序对对换算法优化解,结束条件为临时解πS不能再优化或者迭代次数t超过10. IBSC算法的具体描述如下: 1t=0,TCT=F(π); 2 Repeat Flag=False; Forp=nto 1 对任务πS,[p]调用最佳对换算法JBSP; 如果TCT>F(πS),则 TCT=F(πS),π=πS; 否则 Flag=True,Break; t=t+1; Until (Flag=True ort>10) 3 返回π. IBSC算法的时间开销主要在第2步,其时间复杂度为O(n2),故IBSC算法的时间复杂度为O(n2). 求解最小化总完工时间的无等待流水作业调度问题的ISCH算法步骤如下: ① 参数初始化; ② 根据式(1)生成距离矩阵; ③ 调用ISG算法生成初始解; ④ 调用SGA算法构造解; ⑤ 调用IBSC算法改进解; ⑥ 根据式(2)计算解的目标函数值. ISCH算法的时间开销主要在第②步和第④步.其中,第②步的时间复杂度是O(mn2),第④步的时间复杂度是O(n3),故ISCH算法的时间复杂度为max{O(mn2),O(n3)}. 针对最小化总完工时间的无等待流水作业调度问题,将ISCH算法与BE算法[10]、PH1(p)算法[5]、FNM算法[4]和GA-VNS算法[8]进行比较.同时,为了公平全面地比较ISCH算法和GA-VNS算法,设计了如下2组实验:①限定运行时间的算法比较,即将GA-VNS算法在每个实例上的运行时间近似等于ISCH算法的运行时间,进行算法比较;②不限定运行时间的算法比较,即不限定GA-VNS算法在每个实例上的运行时间,进行算法比较. 所有算法都采用Java语言实现,利用文献[12]中的120个Benchmark实例进行测试,运行于Pentium 2.93 GHz,512 M内存的PC机上. 算法性能指标采用平均相对偏差,其计算公式为[2] (8) 式中,N表示具有相同规模的实例个数;Fz(H)表示采用算法H求解实例z得到的总完工时间;Bz为采用所有比较算法求解实例z得到的最小总完工时间.显然,ARPD值越大,算法性能越差. 在限定GA-VNS算法运行时间的情况下,5种算法的运行时间和性能分别见表1和表2. 表1 限定条件的运行时间比较 s 由表1可以看出,BE算法的运行时间最短,即使对于ta12组的实例,该算法的运行时间也仅仅需要0.403 s.PH1(p)算法、FNM算法和ISCH算法中,ISCH算法的运行时间最短,PH1(p) 算法次之,FNM算法最高,这是因为目标增量法可大大降低ISCH算法的运行时间. 表2 限定条件的ARPD比较 % 由表2可以看出,BE算法的性能明显比其他算法差.FNM算法的平均性能优于PH1(p)算法.当任务数n<100时,ISCH算法的性能比FNM算法差,但明显优于PH1(p) 算法;当任务数n≥100时,ISCH算法的性能最好,其平均ARPD值小于PH1(p) 算法和FNM算法.因此,随着任务数n的增大,ISCH算法能在较短的时间内得到更好的解.尽管在某些小规模实例(如ta03组和ta06组)上,ISCH算法的性能比GA-VNS算法差,但其平均ARPD值较GA-VNS算法提高0.99%(在问题规模较大时,其目标函数值较大,故对解的优化效果很明显),其主要原因是GA-VNS算法的运行时间被限定,搜索空间缩小,故解的性能必然下降. 在不限定GA-VNS算法运行时间的情况下,5种算法的运行时间和性能分别见表3和表4. 表3 无限定条件的运行时间比较 s 表4 无限定条件的ARPD比较 % 将表1和表3相比较,4种启发式算法的运行时间并没有发生变化.由于GA-VNS算法的搜索范围大大增加,故其需要的运行时间远大于4种启发式算法的时间.如当n=500时,GA-VNS算法的平均运行时间约为10 237 s,而ISCH算法仅需不到80 s,前者约为后者的129倍. 由表4可知,无运行时间限制时,GA-VNS算法的性能最优,其平均ARPD值为0.532,高出ISCH算法约1.5%.但由表3可知,GA-VNS算法的运行时间远大于ISCH算法的运行时间. 因此,在实际的大规模调度问题中,如果只追求算法性能,可以采用GA-VNS算法;如果实时性要求很高,则可采用BE算法;如果同时兼顾实时性和性能,则可采用本文提出的ISCH算法. 限定运行时间时,算法的平均性能随任务数和机器数的变化情况分别见表5和表6. 表5 不同任务数下算法平均ARPD值 表6 不同机器数下算法平均ARPD值 由表5可以看出,BE算法、FNM算法和GA-VNS算法的平均ARPD值随着任务数n的增加出现一定的起伏,算法性能不稳定.ISCH算法和PH1(p)算法的平均ARPD值均随着任务数n的增加而逐渐降低,但ISCH算法的初始平均ARPD值优于PH1(p)算法且下降更快.当n>100时,ISCH算法的平均ARPD值小于BE算法、FNM算法和GA-VNS算法.因此,随着任务数n的增加,ISCH算法的性能越来越好. 由表6可以看出,随着机器数m的增加,BE算法和FNM算法的平均ARPD值呈下降趋势,而GA-VNS算法、ISCH算法的平均ARPD值呈上升趋势,PH1(p) 算法的平均ARPD值起伏不大.总体而言,尽管随机器数m的增加,ISCH算法的平均ARPD值在缓慢增大,其平均性能依然优于其他算法,表现出稳定的性能特性,因此ISCH算法适合于求解大规模流水调度问题. 针对最小化总完工时间的无等待流水作业调度,本文提出了一种复合启发式算法.首先,分析了2个任务之间的距离,推导出基本邻域结构操作的目标增量性质;然后,构造了基于插入-分段邻域结构和优化方法,并提出了基于迭代对换的提高解方法.采用经典Benchmark实例,将所提算法与目前经典的启发式算法和最新元启发式算法进行比较.结果表明,ISCH算法在实时性和性能2个方面均能兼顾,即在较短的时间内能得到较好的解,适合于实时大规模无等待流水作业调度系统. ) [1]Laha D,Chakraborty U K.A constructive heuristic for minimizing makespan in no-wait flow shop scheduling[J].InternationalJournalofAdvancedManufacturingTechnology,2009,41(1/2): 97-109. [2]Li X P,Wu C.Heuristic for no-wait flow shops with makespan minimization based on total idle-time increments[J].ScienceinChinaSeriesF:InformationSciences,2008,51(7): 896-909. [3]Rahimi-Vahed A R,Javadi B,Rabbani M.A multi-objective scatter search for a bi-criteria no-wait flow shop scheduling problem[J].EngineeringOptimization,2008,40(4): 331-346. [4]Aldowaisan T,Allahverdi A.New heuristics for m-machine no-wait flowshop to minimize total completion time[J].Omega,2004,32(5):345-352. [5]Framinan J M,Nageno M S,Moccellin J V.An efficient heuristic for total flowtime minimization in no-wait flowshops[J].InternationalJournalofAdvancedManufacturingTechnology,2010,46(9/10/11/12): 1049-1057. [6]Gao K Z,Pan Q K,Li J Q.Discrete harmony search algorithm for the no-wait flow shop scheduling problem with total flow time criterion[J].InternationalJournalofAdvancedManufacturingTechnology,2011,56(5/6/7/8): 683-692. [7]Pan Q K.Tasgetiren M F,Liang Y C.A discrete particle swarm optimization algorithm for the no-wait flowshop scheduling problem[J].Computers&OperationsResearch,2008,35(9): 2807-2839. [8]Jarboui B,Eddaly M,Siarry P.A hybrid genetic algorithm for solving no-wait flow shop scheduling problems[J].InternationalJournalofAdvancedManufacturingTechnology,2011,54(9/10/11/12):1129-1143. [9]Rajendran C,Chaudhuri D.Heuristic algorithms for continuous flow-shop problem[J].NavalResearchLogistics,1990,37(5): 695-705. [10]Bertolissi E.Heuristic algorithm for scheduling in the no-wait flow-shop[J].JournalofMaterialsTechnology,2000,107(1/2/3):459-465. [11]Nawaz M,Enscore E E,Ham I.A heuristic algorithm form-machinen-job flow-shop sequencing problem[J].Omega,1983,11(1):91-95. [12]Taillard E.Benchmarks for basic scheduling problems[J].EuropeanJournalofOperationalResearch,1993,64(2): 278-285.3 ISCH算法
3.1 基本邻域结构的最佳操作
3.2 初始解生成算法
3.3 移位局部优化算法
3.4 构造解算法
3.5 迭代序对对换算法
3.6 ISCH算法
4 算法性能测试
4.1 限定运行时间的算法比较

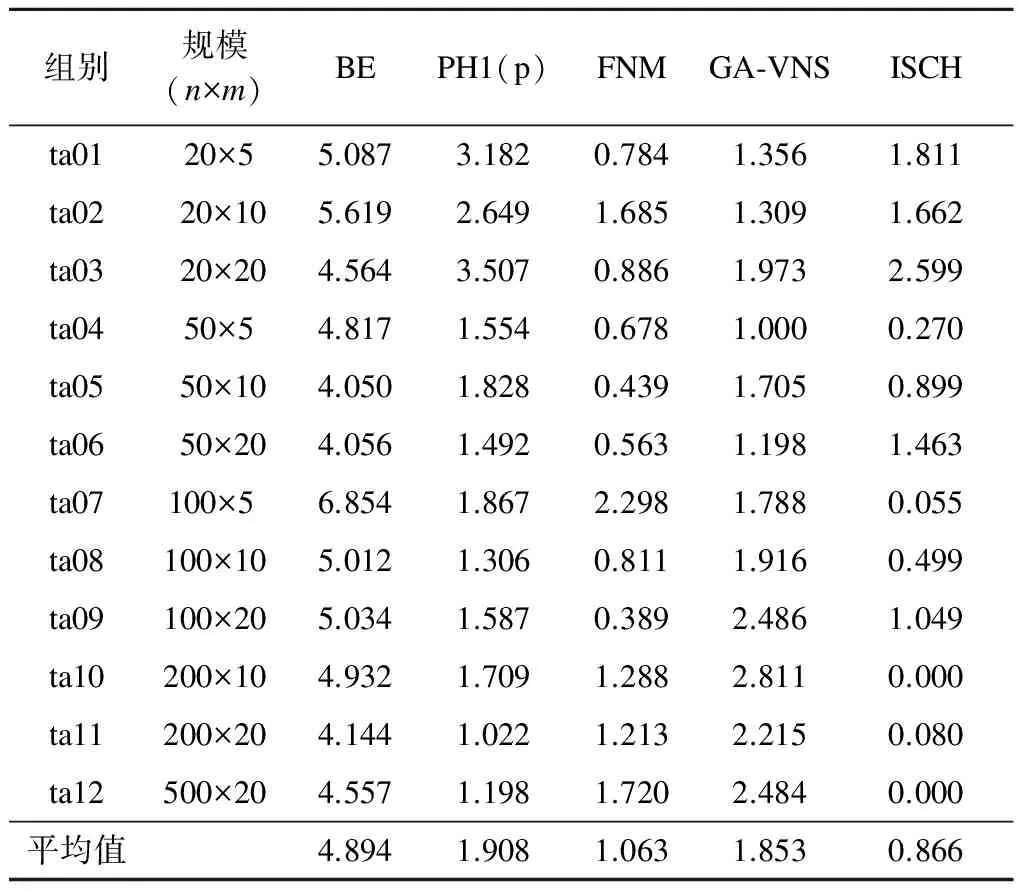
4.2 无运行时间限定的算法比较
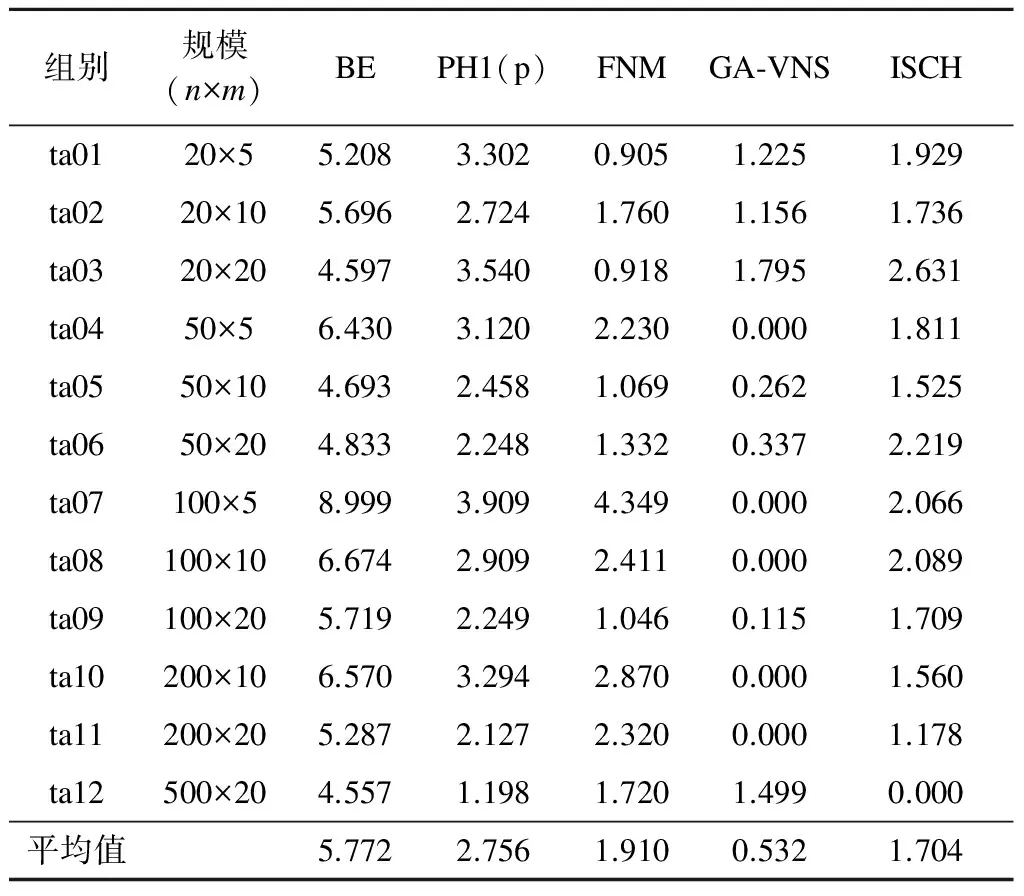
4.3 任务数和机器数对算法的影响
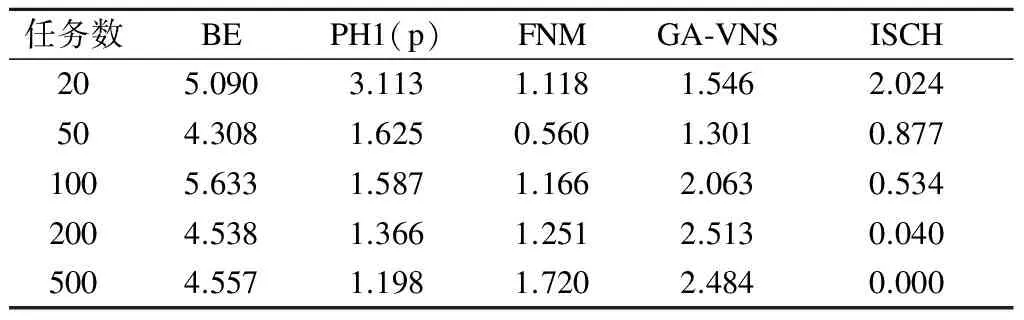
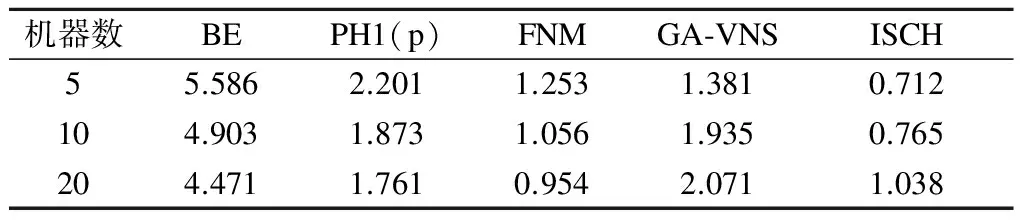
5 结语

