空间两直线平面角与其投影角变化关系的探讨

王续明，邢华璐

(1.华北科技学院机电工程学院，北京东燕郊 101601;2.西北工业大学航空学院，陕西西安 710072)

0 引言

空间一条直线的投影较简单，比如直线AB的长度和它在某一面的投影ab之间的关系符合AB=ab·cosθ，其中θ为直线与投影面之间的夹角，显然AB＞ab。当θ=0°时，直线AB平行于投影面，在该面的投影反应实长。空间两直线的平面角的投影不同于直线段，它可能大于或等于或小于角度本身，它们的内在关系比较复杂，再加上空间位置变化多端，给角度投影的理解和应用带来很大困惑。空间角度的投影分为线面型和线线型，本文所讨论的问题主要针对空间两相交直线的线型。在工程制图的教学中，没有给出解决任意平面角的图解问题，空间两直线的夹角是工程实际中经常碰到的问题，学生在学习过程中对平面角与其投影之间的关系理解不够深刻。笔者在总结前人工作的基础上，应用三射线定理，分类讨论了它们之间的变化规律，以期强化工程制图的教学工作，深化空间角在工程实际中的应用。

1 三射线定理及其在角度投影中的应用

如图1所示，从空间一点P任意引出三条不共面的射线 PA、PB、PC，设∠APC =α，∠BPC=β，∠APB=θ，且二面角A－PCB为ω，则:

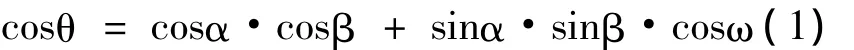
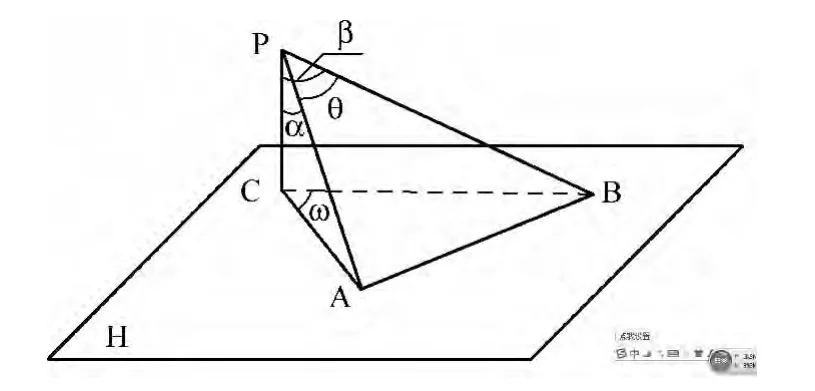
图1 三射线定理空间示意图

式(1)反应空间角∠APB与其在H面上投影角∠ACB的关系，当然通过三角函数也不难推导出此公式。三射线定理也称为三面角的余弦定理，常被记作:

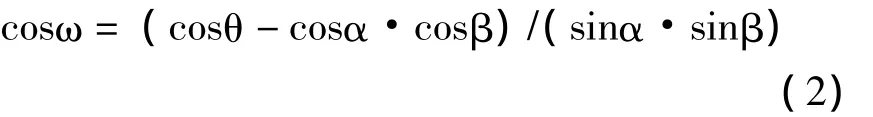
2 讨论

1)直线PC同时垂直于PA与PB，即α=β= 90°

如图2所示，此时两直线PA、PB都与H面平行，那么在H面上的投影角反应空间角度的实际大小，即θ=ω。把上述条件带入公式(2)中，也很容易得出cosω=cosθ，θ=ω的情况。

图2 α=β=90°的空间示意图

2)PC垂直于PA和PB其中的一条边，不妨设β=90°，α≠90°

把以上条件带入公式(2)得到:cosω=cosθ/ sinα。由于符合β=90°，α≠90°的所有情况，可以总结为直线PA绕PB做360°的旋转运动，那么PA在空间经过的轨迹是在一个以PB为轴线、锥顶角为2θ的圆锥面，其中θ是直线PA与PB的平面角。当θ为锐角时，cosθ＞0，由上式得到ω＜θ。如图3所示，A点的投影轨迹与圆锥底面的投影aa'重合，显然投影角ω在0°到θ之间变化，小于空间实际的平面角。

当夹角θ为直角时，在sinα≠0的情况下代入公式cosω=cosθ/sinα得到ω=90°。此情况其实就是工程制图中的直角投影定理，即“互相垂直的两直线，若其中一条平行于某一投影面，则两直线在该投影面上的投影也是直角”。

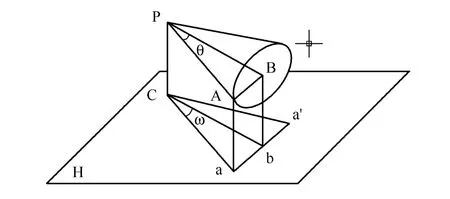
图3 α≠90°且β=90°的空间示意图

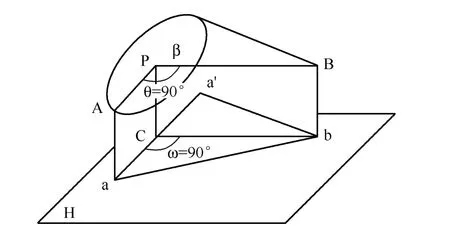
图4 θ=90°的空间示意图

如图4所示，PA⊥PB，则bc⊥aa'，那么ω恒等于90°。在PA旋转的过程中，当直线PA与PC共线时，会出现sinα=0的情况，由于sinα在分母上，所以表达式没有意义，此时空间实际情况是PA的投影积聚在c点上，ω可以看作等于0°。

当直线PA与PB所成的角θ为钝角时，cosθ＜0，由公式cosω=cosθ/sinα得出ω＞θ。空间投影情况如图5所示，A点的投影仍在线段aa'上变化，但此时投影角ω在0°和180°之间变化，大于实际的平面角。

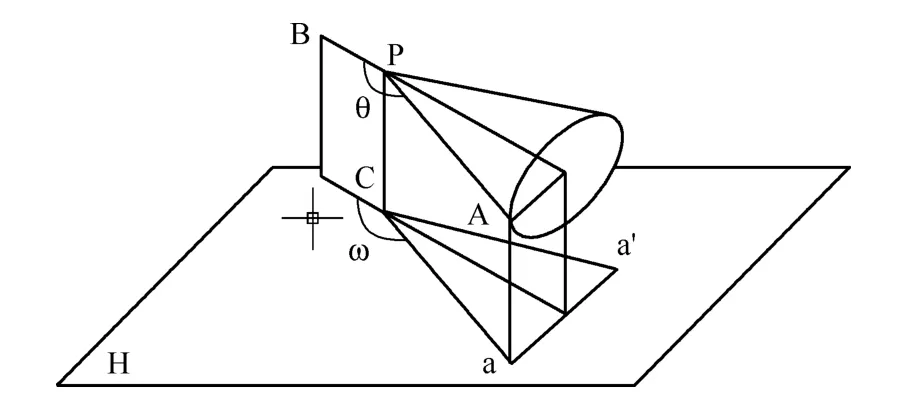
图5 θ＞90°的空间示意图

3)直线PC与两条边都不垂直，即α≠90°且β≠90°

此条件下有一种情况比较特殊，即当PC与PA和PB共面的情况，如图6所示，此时投影比较简单。如果C点在AB之间变化，显然θ=α+ β，则cosθ=cos(α+β)=cosα·cosβ

－sinα·sinβ，带入得到公式(2)得到ω= 180°，这说明不管PA、PB怎么改变，投影角恒等于180°。

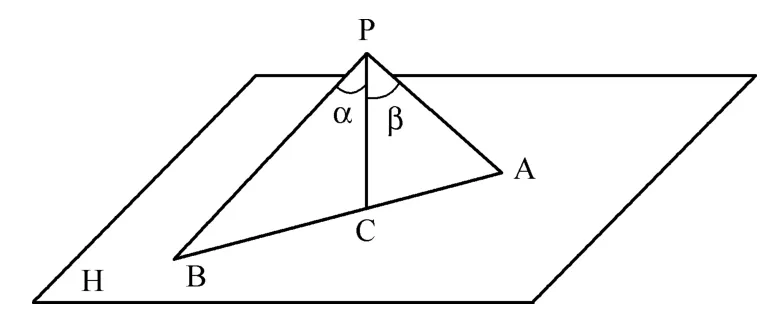
图6 C点在AB之间的空间示意图

当C点在AB之外时，如图7所示，θ=β－α (或θ=α－β)，cosθ=cos(β－α)=cos(β－α) =cosα·cosβ+sinα·sinβ，带入公式(2)得到ω =0°，说明投影角恒等于0°，不随α、β的变化而改变。

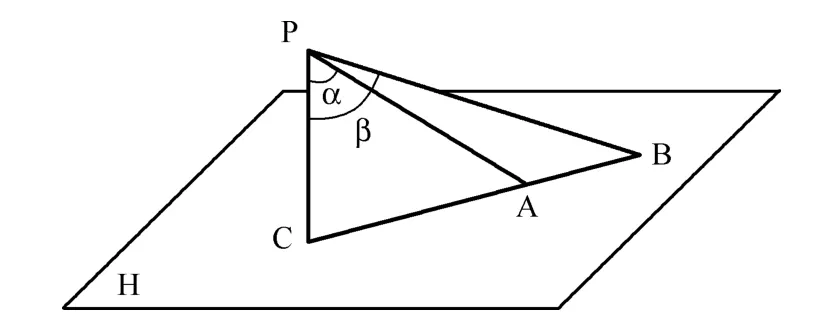
图7 C点在AB之外空间的示意图

除了上述的这种共面情况外，其他情况就相对比较复杂，通常工程制图的解题思路是利用换面法把空间平面角的一条边变换成投影面的平行线，然后运用相应的投影规律进行解题。这里不用投影变换，先假定投影角ω为一定值(不妨设ω=90°)，然后研究α、β与θ之间的变化关系。把ω=90°带入公式(2)得到:

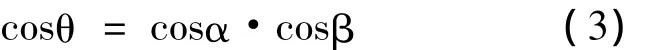
显然θ是α、β的二元连续函数，θ在［0°，90°］内取值时，都会找到一组α、β值与之相对应。具体变化情况是怎么样的呢?先假定PA、PB都在P点的下侧，那么α和β都在［0°，90°］变化，笔者用matlab软件绘制出了θ=0、π/6、π/3、π/2时的曲线见图9所示。可以看出，每一个θ值都对应一条曲线，只要适当调整α、β的大小，让它们落在相应的曲线上，就能满足给定的θ值，而且满足此条件的空间位置有很多个。

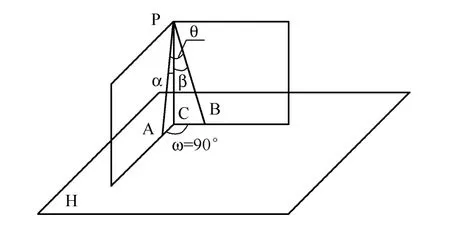
图8 两直线在P点下侧的空间示意图

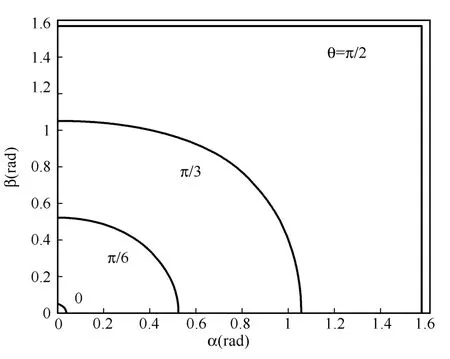
图9 平面角θ为锐角时的曲线簇

θ在［90°，180°］取值时，cosθ的值为负数，此时PA与PB应该分别位于P点的上下两侧，不妨设PA在P点下侧，PB在P点上侧，即α在［0°，90°］变化，β在［90°，180°］变化。同理绘制出θ=π/2、5π/6、2π/3、π时的曲线见图11所示，这组曲线与上面那组曲线是以β=π这条线对称分布的。θ取最小值0°的情况是α=β= 90°，即PA、PB都与PC重合;θ取最大值180°的情况是α=90°，β=0°，则PA与PC重合，PB与PC的反方向重合。

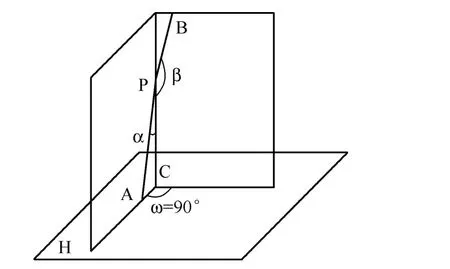
图10 两直线在P点上下两侧空间的示意图

综上所述，对于任意给定的投影角ω，可以在空间中找到任意大小的平面角θ，并且满足此平面角θ的位置有很多个，只需让α和β沿着相应的曲线变化即可。总而言之，这种情况空间平面角可以大于、等于或小于其投影角，它们之间的关系不确定。

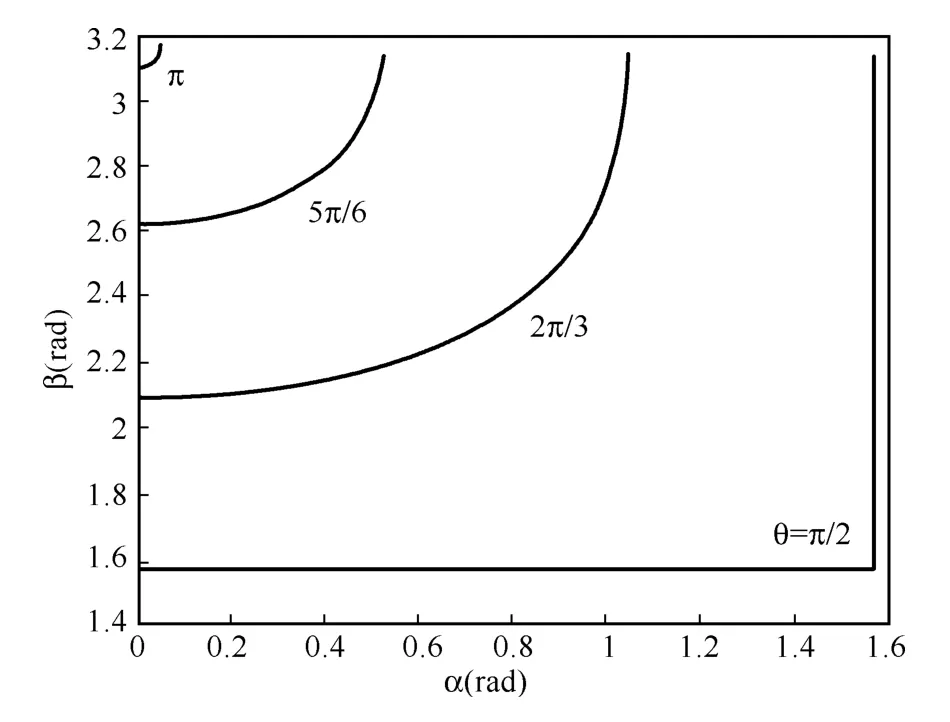
图11 平面角θ为钝角时的曲线簇

3 结论

1)两直线PA、PB都与H面平行，那么在H面上的投影角反应空间角的实际大小，即ω=θ。

2)如果两直线PA、PB中的一条平行于H面，当θ为锐角时，0°＜ω＜θ;当θ为直角时，ω= 90°，特殊情况 ω=0°;当 θ为钝角时，θ＜ω＜180°。

3)当两边都不平行于投影面时，对于任意给定的投影角度值，可以在空间中找到［0°，180°］任意大小的平面角，而且每个平面角所对应的位置也存在很多个，只要让α和β的关系沿着曲线变化即可。这种情况空间平面角可以大于、等于或小于其投影角，它们之间的关系不确定。

4)本文只是针对平面角的水平投影行了分析，实际三面投影中，还需要分析其他两投影面的情况，运用三面角余弦定理，再结合三面角的正弦定理，就可以解决空间角度的解析计算问题。将所求空间角度的关系分析清楚，然后把相应的计算方法编写成程序，这对工程实际来说是非常便捷和实用的。

［1］ 周万民.投影成直角的空间平阿角讨论［J］.东北重型机械学院学报，1988，(3):85.

［2］ 高崇仁.空间角度的投影与计算［J］.甘肃工业大学学报，1989，15(3):84－89.

［3］ 高崇仁.空间角度的精确计算［J］.西北师范大学学报，1989:19－22.

［4］ 白春光.关于空间角度计算的新方法［J］.机械工程师，1994，(06):16－17.

［5］ 张永波.用投影法计算空间角度［J］.内江科技，2011，(05):10.