(3+1)维三次-五次Gross-Pitaevskii方程在非对称势阱下的精确解
纪庆群, 陈 浩
(华南师范大学物理与电信工程学院,广州 510006)
Gross-Pitaevskii方程(GPE)是玻色爱因斯坦凝聚中的一个重要模型,用来描述凝聚物物质波的函数[1]. 另外,在光纤、等离子物理、流体力学中也具有重要作用. 研究GPE得出了一些可行的解法[2-3]. 例如:广田法、雅克比椭圆函数法、自相似变换和F展开法. (1+1)维GPE的稳定孤子解已经得出,并已在实验中得到验证[4].
近年来,当势阱为抛物线形,散射系数为常数时,得到一系列的周期解和行波解.如考虑两体和三体相互作用时各向同性下GPE的自相似解[6]、通过数据值计算[7]或自相似变换[8]得到雪茄型势阱下(3+1)维GPE的精确解.但仅考虑易轴或易平面对称,很少考虑3个方向的各向异性.
本文采用F展开法和齐次平衡法[9]求解3个方向各向异性的GPE,得出雅克比椭圆函数解.讨论了一些解的动力学性质和各向异性对孤子的影响.
1 Gross-Pitaevskii方程及其解法
考虑如下的(3+1)维三次-五次GPE:
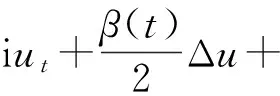
V(x,y,z,t)u=iγ(t)u,
(1)
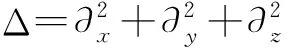
式(1)可以写成振幅和相位的形式
u(x,y,z,t)=A(x,y,z,t)exp[iB(x,y,z,t)],
(2)
把式(2)带入式(1)中,可以得到耦合方程:
(3)
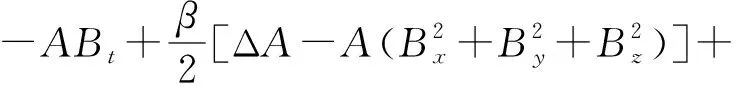
(4)
根据齐次平衡法,做如下变换:
(5)
把式(5)带入式(3)、(4)可得
ρt+β[ρxBx+ρyBy+ρzBz+ρΔB]=2γρ,
(6)
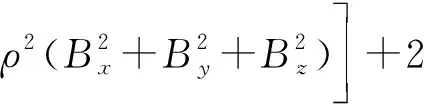
(7)
用F展开法把解展开为:
ρ=f1(t)+f2(t)F(θ),
(8)
θ=k1(t)x+k2(t)y+k3(t)z+w(t),
(9)
B=a1(t)x2+a2(t)y2+a3(t)z2+b1(t)x+
b2(t)y+b3(t)z+e(t).
(10)
其中,fj、ki、w、ai、bi和e(i=1,2,3;j=1,2)均为时间的函数,F是第一类雅克比椭圆函数,F′2=c0+c2F2+c4F4.
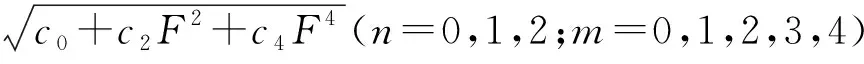
fjt+2(a1+a2+a3)βfj-2γfj=0,
(11)
kit+2βaiki=0,bit+2βaibi=0,
(12)
(13)
wt+β(k1b1+k2b2+k3b3)=0,
(14)
(15)
(16)
(17)
(18)
(19)
在一些约束条件基础上,解式(11)~(19),得到:
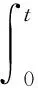
(20)
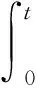
(21)
(22)
(23)
其中,i=1,2,3,j=1,2.ki0、bi0、w0和e0是t=0时刻各函数的初始值. 当f10=0时δ=0,否则δ=1. 需要注意的是非线性系数1、2必须满足以下2个约束条件:
a1-a2-a3)dt],
(24)
a1-a2-a3)dt].
(25)
这些式可以理解为式(1)的2个可积条件. 另外,需要注意的是c0、c2和c4必须满足
(26)
若要得到孤子解,则雅克比椭圆函数满足:c0+c2+c4=0. 结合式(26),可得
f20=±f10.
(27)
从式(5)、(6)可以看出f10是正常数,推出1.2是负数. 意味着两体相互作用和三体相互作用是相互竞争关系. 从式(20)~(25)可以看出系数和参数均依赖于ai,可以从式(13)中求出ai,然而对于一般的α和β,式(13)没有具体的解. 为了解这个方程,α和β必须满足特定的关系. 本文假设α/β=α0/β0,α0和β0是同号常数.
2 结果与分析
通过假设α/β=α0/β0,得到精确解:
(28)
(29)
(30)
(31)
(32)
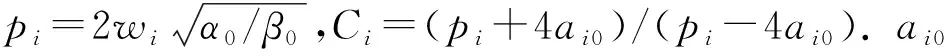
(b1x+b2y+b3z)+e]},
(33)
式中,
θ=w0+k1x+k2y+k3z-
(34)
3 讨论
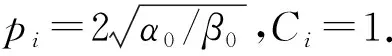
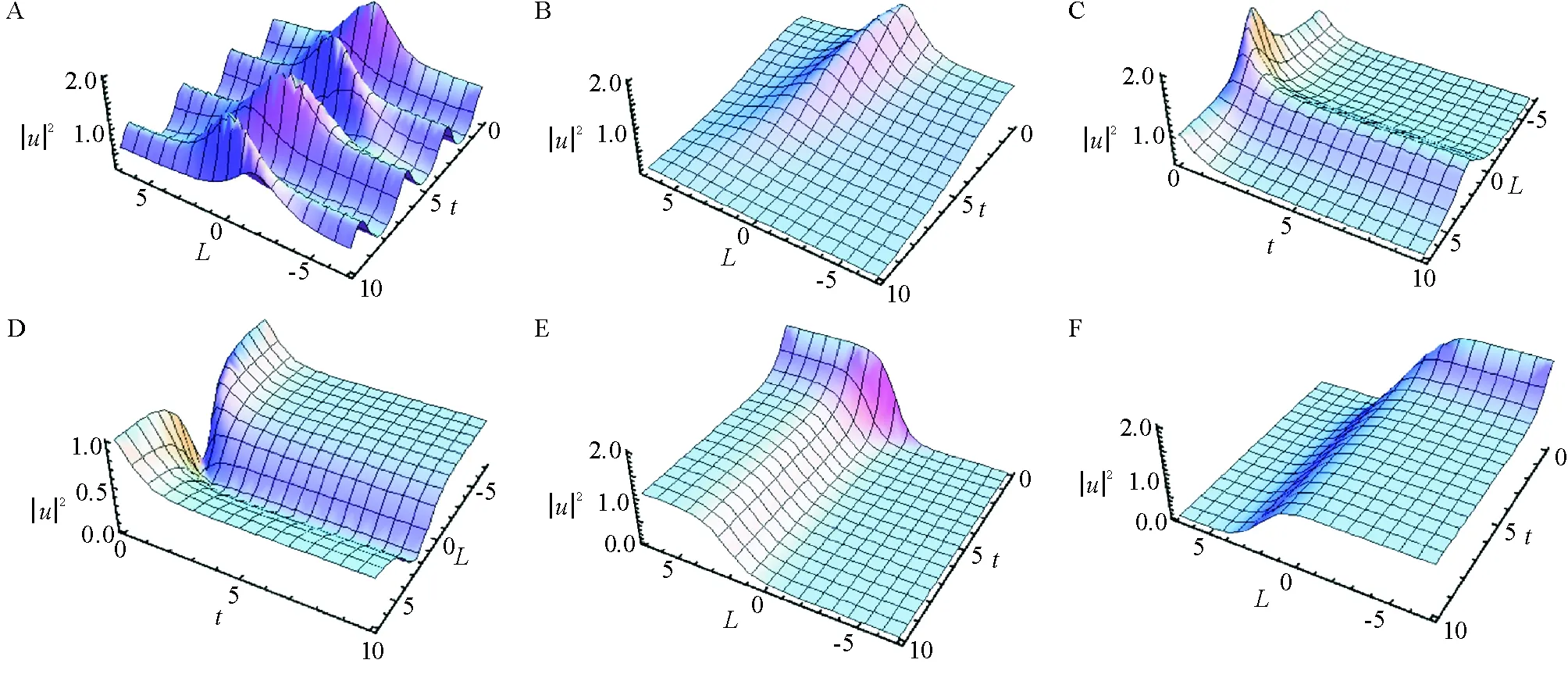
图1 呼吸子解(A)、衰减的孤子解(B)、亮孤子解(C)、暗孤子解(D)、扭结子解(E)、反扭结子解(F)
值得注意的是,若考虑β=β0e-εt情况,孤子的振幅和宽度均随时间变小,并趋于某一固定值,孤子的传播方向也逐渐稳定. 一段时间后,孤子传播稳定,尽管此时没有增益. 如选择β=e-1.5t,可得亮孤子解和暗孤子解. 此时图1C中f20=1,图1D中f20=-1. 其它参数和系数与图1A、B相同.
图1E、F为相互对称的扭结子和反扭结子. 参数和系数除了F(θ)=tanh(θ)外与图1C、D相同.
考虑势阱各向异性的情况,假设w⊥=w1=w2,当势阱为盘面形(w3>>w⊥)时,式(1)转变为准二维GPE. 当势阱为雪茄型(w3< 图2A~D显示了在w3逐渐增大时孤子形状的变化. 振幅逐渐减小,朝逆时针方向转动,并趋于水平. 由图2E~H可知,孤子的宽度逐渐增加,说明凝聚物的密度在减小. 当w⊥逐渐增大时,也得到类似情况. 需要注意的是,此时孤子沿顺时针转动并趋于垂直. 图2 孤子波形的变化 本文解出了广义的(3+1)维GPE,得出了一系列雅克比椭圆函数解.选择不同的β时,可得到不同类型的孤子解. 当β选择指数形式时,孤子趋于稳定的值. 讨论了各向异性对孤子动力学的影响,发现在各向异性时,孤子的形状和稳定性存在显著变化. 参考文献: [1] Dalfovo F, Giorgini S, Pitaevskii L P, et al. Theory of Bose-Einstein condensation in trapped gases[J]. Reviews of Modern Physics, 1999, 71(3):463-512. [2] Kobayashi M, Tsubota M. Kolmogorov Spectrum of superfluid turbulence: Numerical analysis of the Gross-Pitaevskii equation with a small-scale dissipation[J]. Physical Review Letters, 2005, 94(6): 5302-5306. [3] Zhong W P, Belicé M R, Lu Y Q, et al. Traveling and solitary wave solutions to the one-dimensional Gross-Pitaevskii equation[J]. Physical Review E, 2010, 81(1):6605-6609. [4] Atre R, Panigrahi P K, Agarwal G S. Class of solitary wave solutions of the one-dimensional Gross-Pitaevskii equation[J]. Physical Review E, 2006, 73(5):6611-6615. [5] Petrovic N Z, Belic M, Zhong W P. Spatiotemporal wave and soliton solutions to the generalized (3+1)-dimensional Gross-Pitaevskii equation[J]. Physical Review E, 2010, 83(1):6610-6614. [6] Dai C Q, Chen R P, Wang Y Y. Spatiotemporal self-similar solutions for the nonautonomous (3+1)-dimensional cubic-quintic Gross-Pitaevskii equation[J]. Chinese Physics B, 2012, 21(3):508-513. [7] Perez V M, Michinel H, Herrero H. Bose-Einstein solitons in highly asymmetric traps[J]. Physical Review A, 1998, 57(5):3837-3842. [8] Wang D S, Li X G. Localized nonlinear matter waves in a Bose-Einstein condensate with spatially inhomogeneous two- and three-body interactions[J]. Journal of Physics B, 2012, 45(10):5301-5308. [9] Chen Y X, Lu X H. Spatiotemporal similaritons in (3+1)-Dimensional inhomogeneous nonlinear medium with cubic-quintic nonlinearity[J]. Communications in Theoretical Physics, 2011, 55(5):871-877. [10] Abdullaev F K, Gammal A, Tomio L, et al. Stability of trapped Bose-Einstein condensates[J]. Physical Review A, 2001, 63(4):3604-3617. [11] Zhang A X, Xue J K. Band structure and stability of Bose-Einstein condensates in optical lattices with two- and three-atom interactions[J]. Physical Review A, 2007, 75(1):3624-3629.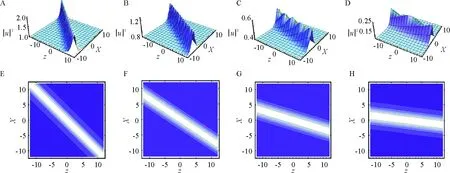
4 结论

