一类椭球等高矩阵分布的二次型
郭春香,王 青
(1.常州机电职业技术学院基础部,江苏 常州 213164;2.常州机电职业技术学院 电气工程系,江苏 常州 213164)
椭球等高分布作为正态分布的推广,它拥有许多类似于多元正态分布的优美性质。文献[1]中给出的向量球对称分布的定义和相关定理,成为研究样本分布的有力工具;文献[2]中给出了向量球对称分布的F分布,文献[3]中给出了与向量球对称分布有关的一类广义卡方分布,这些理论为进一步研究向量球对称分布提供了理论基础。本文在文献[2]和文献[3]的基础上研究了向量球对称分布和一类椭球等高矩阵分布的二次型,应用典型方法求出了二次型及其逆的密度函数,从而丰富了样本理论的研究,为解决复杂样本统计量的分布问题提供了一定的理论基础。
定理1 设矩阵X有密度,则X~VSn×p(φ)当且仅当X的密度形为f(tr(X'X)).
若X ~ VSn×p(φ)且X有密度f,则我们就记X ~ VSn×p(f).
引理1 设X是n×p矩阵,且T∈UT(p),则:

其中,Dp={T|T∈UT(p)}且有正对角元素,Γp(·)是多元Gamma函数,并且
引理2[4]若Y>0,它的乔列斯基分解Y=X'X,其中X为n阶上三角阵,且对角元素为正,则:

定理2 设X ~ VSn×p(f),n≥p,即X有密度f[tr(X'X)],则W=X'X的密度是:

证明:设h(·)是任意非负Borel函数,则:

由引理1,有:

所以,W=X'X的密度是:

引理 3 设 X=Y-1,Ym×m对称,则:

定理3 设X ~ VSn×p(f),n≥p,则V=W-1=(X'X)-1的密度是:
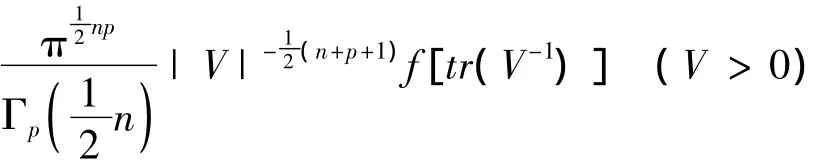
证明:由定理2可知,若X ~VSn×p(f),则W=X'X的密度是:

令 V=W-1=(X'X)-1,则 W=V-1,J(W → V)=|V|-(p+1),从而,我们有 V=W-1=(X'X)-1的密度是:

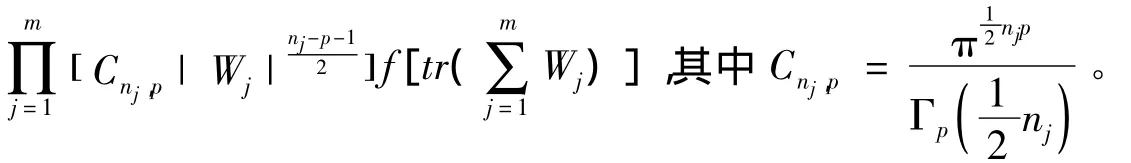
证明:由引理1知,对任意非负Borel函数h(·),有:


从而,有:


定义2 设Y=M+XB,其中X~VSn×p(φ),B:p×q,M:n×q,则我们说Y遵从椭球等高矩阵分布,记为 Y ~ EVSn×q(M,B,φ)或 Y ~ EVSn×q(M,B,f)。
因此,Y的分布只通过∑ 依赖于B,我们把VSn×q(M,B,φ)记为VSn×q(M,∑,φ)。
引理5[5]若Y=AXB ,其中 Y:n × p,X:n × p,A:n × n,B:p× p,且A,B 可逆,则:



所以,Y的密度是:

引理6[6]若 X,Y均为 n × n阵,|B|≠0,Y=B'XB 且 X'=X ,则:

推论1 设Y ~ EVSn×q(0,∑,f),其中n≥q,∑ >0,则W=Y'Y的密度是:

证明:由定理2知,若X ~VSn×q(f),则L=X'X的密度是:

因为Y ~EVSn×q(0,∑,f),故由定义2知Y=XB,其中X ~VSn×q(f),从而有
所以,W=Y'Y的密度是:

推论2 设Y ~ EVSn×q(0,∑,f),其中n≥q,∑ > 0,则V=W-1=(Y'Y)-1的密度是:

证明:由推论1知,若Y ~ EVSn×q(0,∑,f),则W=Y'Y的密度是:
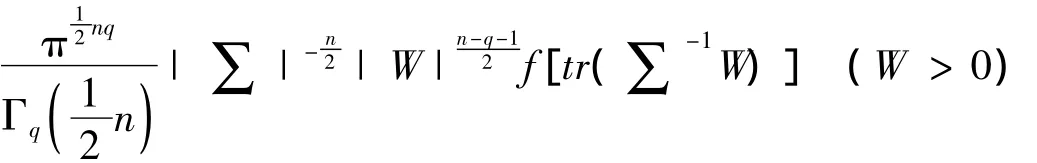
从而我们有V=W-1=(Y'Y)-1的密度是:




并且有


[1]方开泰,张尧庭.广义多元分析[M].北京:科学出版社,1993.
[2]郭春香.向量球对称分布的F分布[J].金陵科技学院学报,2010,26(2):10-13.
[3]郭春香,王青.与向量球对称分布有关的一类广义χ2分布[J].金陵科技学院学报,2012,28(1):5-8.
[4]朱道元,吴诚鸥,秦伟良.多元统计分析及软件SAS[M].南京:东南大学出版社,1999.
[5]杨琳.逆非中心Wishart分布[D].南京:东南大学数学系,2009.
[6]徐海燕.一类矩阵椭球等高分布的广义二次型[J].金陵科技学院学报,2008,24(2):7-9.

