Riemann边值在不同共形映射下的等价变换

江清华

（贵州师范大学数学与计算机科学学院，贵州 贵阳550001）

0 引言及主要结果

本文是研究解析函数边值问题中的一种周期Riemann边值问题，首先读者应该熟悉Plemelj公式及其广义公式，它们是研究边值问题的基本工具.为了文章的后续内容的证明与陈述，读者必须熟悉且掌握解析函数边值问题研究中的一些基本符，相关定理，命题和定义。

1 Hold条件定义

1.1 设f(t)定义于（开口或封闭）光滑曲线L上，若对其上任意两点t1，t2恒有α，(0＜α≤1)，A,α 都是确定的常数, 则称 f(t)在L上满足α阶的Hold条件或Hα条件,记为f(t)∈Hα(L)或简记为f∈Hα,α称为Hold指数,也可以记为f(t)∈H(L)也可以这样理解：,当α=1时，条件H1也称为Lipschitz条件.文章中讨论的解析函数都是在H上进行的.

1.3 设L是有限条互不相交的封闭曲线的集合，它把全平面分割成有限个区域。F(z)是这样一个函数，它在每个这样的区域中全纯，在点z=∞处至多有一个极点，且当z从L的任意确定的侧趋于L上的任何点时，F(z)的极限值即边值存在，则称F(z)是以L为跳跃（或间断）曲线的分区全纯函数。如果L中含有开口弧段，则要求在各端点附近，F(z)有不到一阶的奇异性，即若c为L的一端点，则在z=c附近，为常数。 在点 z=∞ 处，F(z)的 Laurent展式为：F(z)=,则称F(z)在点z=∞处为k阶的或阶数为 k。当 k＞0时，它以z=∞为k阶极点；当k＜0时，它以 z=∞为-k阶零点；k=0时，表示F(∞)≠0且有限。因此分区全纯函数F(z)要求在z=∞处有有限阶。

1.4 设z从封闭曲线L的正向（逆时针旋转方向）的左侧趋于L上某点t时（不包括开口弧段的端点）F(z)的边值存在记为F+(t)，而当z从L的负向（顺时针旋转方向）趋于t时，边值记为F-(t)；而把φ(t)=F+(t)-F-(t)称为F(z)在t处的跳跃或跃度，φ(t)关于t的函数，称为跳跃函数。

1.5 在Riemann边值问题中涉及到解的一般形式，设，其中Pm(z)为任意m次多项式，即在这个解中含有m+1个任意复常数，我们称它是有m+1个复的自由度。(见[3])

1.6 一个分区全纯函数 X(z)满足以下三个性质：（1）X+(t)=G(t)X-(t)；（2）在整个有限复平面上 X(z)≠0，包括在L上X±(t)≠0；（3）在点 z=∞ 处 X(z)有有限阶，则称X(z)为一个Φ+(t)=G(t)Φ-(t)，t∈L的一个典则函数。

1.7 设L是一条逐段光滑的曲线，f(t)∈H于L上，则对于任何t0∈L(当L为开口曲线时，t0不为端点)，Cauchy型积分的边值存在，且有下列 Plemelj公式：；其中 F+(t0),F+(t0)表示 F(z)当 z 分别从 L 的正侧和负侧趋于t0时的极限值，而θ0是L在t0处的两单侧切线在L正侧所张的角(0≤θ0≤2π).特别注意，当t0是L上的光滑点时，或者整个L是光滑曲线，则上述两等式可合写成为：

2 定理

2.1 定理1

如果 Φ(±∞i)有界，则齐次的周期 Riemann边值问题：Φ+(t)=G(t)Φ-(t)+g(t)，g(t)≡0。当指标 κ≥0 时有 κ+1 个线性无关的解；当 κ＜0 时只有零解。

2.2 定理2

如果Φ(±∞i)有界，则非齐次的周期Riemann边值问题：Φ+(t)=G(t)Φ-(t)+g(t)，t∈L。 当 κ≥-1时，其一般解中含有 κ+1个任意常数；当 κ＜-1时，当且仅当满足-κ-1个条件有唯一解，解的自由度为κ+1。

3 主要结果的证明

3.1 准备工作

在涉及到解析函数边值问题时，通常会遇到所谓的Riemann周期问题，在此简记为PR 问题。 设 Li（i=0,±1,±2,…）为无穷条封闭光滑曲线，它们彼此形状相同，互不相交，且以kπ（k＞0）为周期水平地排列，Li均以逆时针方向为正方向。记的内部记为，外部记为。不妨设原点,而；这样可以办得到的。周期Riemann边值问题为：求一个以kπ为周期的分区全纯函数Φ(z)，以L为跳跃曲线（此时 z=∞ 不能为极点），使得 Φ+(t)=G(t)Φ-(t)+g(t)，t∈L，其中 G(t)，g(t)在 L 上都属于 H，且 G(t)≠0，它们都是以 kπ 为周期的：G(t)=G(t+kπ)，g(t)=g(t+kπ)，当时 g(t)≡0 称为齐次的；否则，称非齐次的。[3]z=∞点是各曲线Li之并所成点集的聚点，在z=∞处一般无极限，当 z=±∞i是指 z=x+yi，x为任意的值，y→±∞，此时可以对 Φ(z)赋予一定的条件就可以满足需求。在问题当中，我们只要求Φ(z)也是以kπ为周期，在适当的环境下可以做的，因为对于齐次而言，若Φ1(z)是它的一个非零周期解，但是对于非周期整函数I(z)来说，Φ(z)I(z)也是它的解，但不是具有周期性的解。首先我们作一个共形映射把问题：转化为普通的Riemann边值问题，作带形区域S0：，设L0位于S0之中，并在直线上取定正方向，使位于其右侧，若Φ(z)为PR问题的解，其在S0中部分记为Φ0(z)是S0中的分区全纯函数，可以连续至两直线：上，以L0为跳跃曲线，且满足下列两等式：反之，若Φ0(z)在S0中分区全纯且连续至两直线：

3.2 定理1的证明

在此篇文章中，限制 Φ(±∞i)有界，亦即 Φ*(ζ)在 ζ=0,∞ 处有界，从而正则，根据通常的Riemann边值问题的结果（现在是在R0中求解），这时此式：的解为：，其中，当指的是 Γ0内域)时，；当指的是 Γ0的外域） 时，， 在这里的，而且 Pκ(ζ)为 κ 次任意多项式（当 κ＜0 时，记。现在再回过头来考虑z平面则有：，其中，（1）当时，；

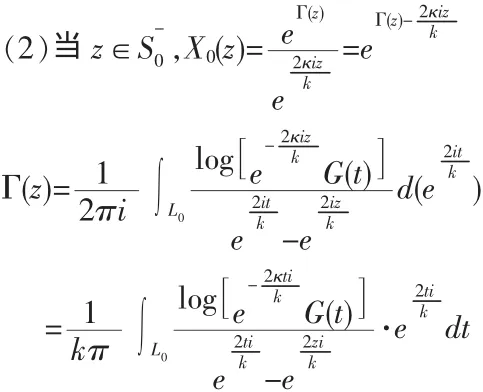
把常系数eC并入到多项式中，因此可以认为：。其中对数可以任取定一支，将Φ0(z)作周期延拓，则周期Riemann边值问题的一般解形式为仍称为PR问题的典则函数，(见[4])上述一般解也可以用另外一种形式替代，是用到分区全纯函数的概念进行表达的：当；当 z∈S-时，，其中是关于以为变量的 κ 次任意多项式（κ＜0,Qκ≡0），证毕。

3.3 定理2的证明

［1］杜金元.广义∏PHBaπOB定理及Plemelj公式的简单证明[R].数学研究报告(武汉大学),1980,5：43-50.

［2］L.V.Ahlfors.复分析[M].赵志勇,薛运华,杨旭,译.机械工业出版社,2005,7.

［3］路见可.解析函数边值问题[M].武汉大学出版,2004,10.

［4］闻国椿.共形映射与边值问题[M].北京：高等教育出版社,1985,10.

［5］钟玉泉.复变函数论[M].高等教育出版社,2003,6.

［6］章红梅,王传荣.Riemann边值问题的解关于边界曲线的稳定性[J].福州大学学报,2001,29：1-4.