求解二维扩展Fisher-Kolmogorov方程的线性化紧差分格式

李 娟， 高广花

(1.应天职业技术学院 基础部，江苏 南京210023;2.南京邮电大学 理学院，江苏 南京210023)

考虑如下二维扩展的Fisher-Kolmogorov 方程的初边值问题:

其中，Ω = (0，1］× (0，1］，T ＞0，f(u)= u3－ u。

当γ = 0 时，方程(1)是由Fisher 和Kolmogorov在1937 年提出的，用来描述生物的扩散与适应间的相互作用。Coullet 和Dee 发现了模型中的一些缺陷，添加了四阶导数项，得到EFK 方程(1)。

EFK 方程已经有了广泛的应用，如双稳态系统的图式形成、总体遗传学、液晶中畴壁的传播问题、反映扩散中的行波等，所以备受关注。文献［1-4］对该方程进行了理论研究。文献［5-11］讨论EFK 方程的数值算法，但是收敛精度仅在空间、时间二阶收敛，且对于二维问题的讨论较少。

为了提高差分格式的收敛精度，文中讨论求解问题(1)～(3)的三层线性化紧差分格式，该方法不仅能够快速地求解方程，而且收敛精度达到时间方向二阶收敛、空间方向四阶收敛。

1 差分格式

取正整数M，N，记h = 1/M，τ = T/N，xi= ih，yj= jh，0 ≤i，j ≤M，tk= kτ，0 ≤k ≤N，Ωh= {(xi，yi)| 0 ≤i，j ≤M}，Ωτ= {tk| 0 ≤k ≤N}。设Uh={| 0 ≤i，j ≤M，0 ≤k ≤N}是定义在Ωh×Ωτ上的网格函数。

对任意的网格函数u ∈Uh，引入如下记号:

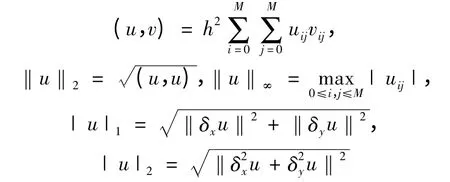
下面引入几个引理。

引理1［12］记α(s)= (1 －s)3［5 －3(1 －s)2］，如果g(x)∈C6［xi－1，xi+1］，则有

引理2［13］对于任意的u，v ∈，有

令

则问题(1)～(3)等价于下面问题:

在Ωh×Ωτ上定义如下网格函数:0 ≤i，j ≤M，0 ≤k ≤N。在()处分别考虑方程(4)，(5)，并应用泰勒展式和引理1，可得

其中

且存在不依赖于h，τ 的正常数c1，使得

在(xi，tk)处分别考虑方程(4)，(5)，并应用泰勒展式和引理1，可得

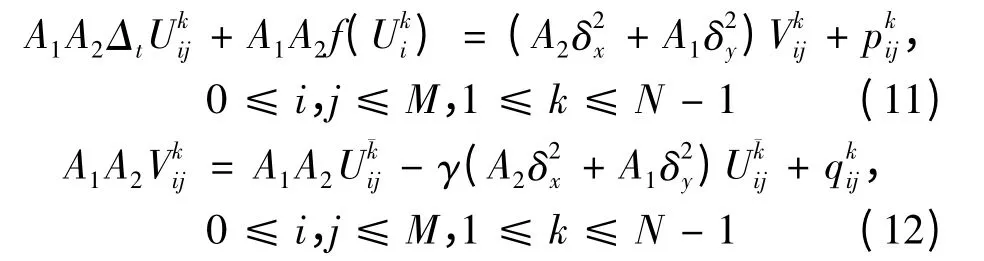
且存在不依赖于h，τ 的正常数c2，使得

根据式(6)，(7)可得

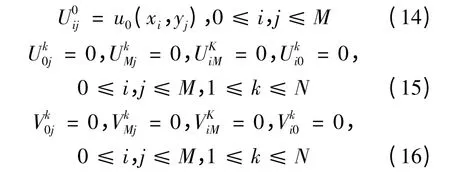
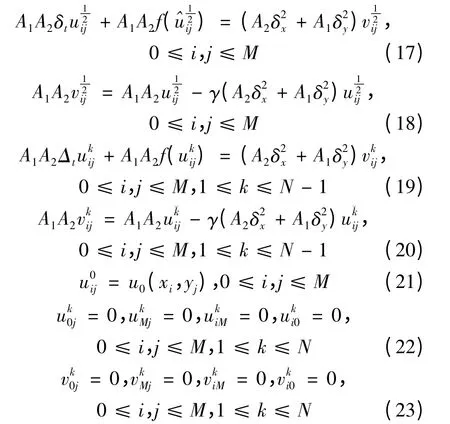
在式(17)～(23)中消去vk，可得到与之等价的差分格式:

采用能量分析法，利用数学归纳法及引理2，可以证明差分格式(24)～(27)是唯一可解的，并且在L∞范数下，空间方向四阶收敛，时间方向二阶收敛。

定理1 差分格式(24)～(27)有唯一的解。

定理2 假设问题(1) ～ (3)的解u(x，t)∈C(6，6，3)(Ω ×［0，T］)，则差分格式(24)～(27)的解按无穷范数收敛于问题(1)～(3)的解，且收敛阶为O(τ2+ h4)。

2 数值算例

在问题(1)～ (3)中取参数r = 0.1，初值u0(x，y)=［100x2(1 －x)2(x －0.5)］·［100y2(1 －y)2(y － 0.5)］。取空间和时间步长分别为h =1/20，τ = 1/ 1 000。采用高斯赛德尔迭代法求解差分格式(24)～(27)，容许误差设定为10－12。差分格式的数值解如图1 所示。

图1 当T = 0.1 时差分格式(24)～(27)的数值解Fig.1 Some numerical results of (24) ～ (27)when T =0.1

由于无法计算其精确解，采用下面方式验证差分格式空间方向四阶收敛:记

若O(τp)充分小，则

记

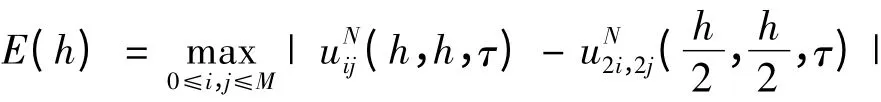
则

在PC 机上利用Matlab 编程，验证出差分格式(24)～(27)在空间方向上四阶收敛。具体数值结果如表1 所示。

表1 当T = 0.1，τ = T/30 000 时差分格式(24)～(27)的数值结果Tab.1 Some numerical results of (24) ～ (27)when T =0.1，τ = T/30 000

3 结 语

文中给出了求解二维扩展的 Fisher-Kolmogorov 方程的三层线性化紧差分格式，并通过数值算例，说明空间方向收敛阶优于目前已有的工作。文中所采用的数值算法，可以推广到更高维的情形。

［1］Andreu F，Caselles V，Mazon J M. A Fisher-Kolmogorov equation with finite speed of propagation［J］. Journal of Differential Equations，2010，248(10):2528-2561.

［2］Kudryashov N A，Zakharchenko A S.A note on solutions of the generialized Fisher equation［J］. Applied Mathematics Letters，2014(32):53-56.

［3］马丽蓉，徐天华，帅维成. 二维Extened Fisher-Kolmogorov 方程的全局吸引子［J］. 西南大学学报:自然科学版，2012，34(8):108-111.

MA Lirong，XU Tianhua，SHUAI Weicheng.Existence and uniqueness of solution for two dimensional extened fisher-kolmogorov equation［J］.Journal of Southwest University:Natural Science Edition，2012，34(8):108-111.(in Chinese)

［4］Juan Belmonte-Beitia，Gabriel F Calvo，Víctor M Pérez-García.Effective particle methods for Fisher-Kolmogorov equations:theory and applications to brain tumor dynamics［J］. Commun Nonlinear Sci Numer Simulat，2014 (19):3267-3283.

［5］JMacías-Díaz J E，Puri A.An explicit positivity-preserving finite-difference scheme for the classical Fisher-Kolmogorov-Petrovsky-Piscounov equation［J］.Applied Mathematics and Computation，2012(218):5829-5837.

［6］El-Azab M S.An approximation scheme for a nonlineardiffusion Fisher’s equation［J］.Applied Mathematics and Computation，2007(186):579-588.

［7］Danumjiaya P，Pani A K. Numerical methods for the extended Fisher-Kolmogorov equation ［J］. International Journal of Numerical Analysis and Modeling，2006，3(2):186-210.

［8］Aprahamian M，Souroujon D，Tersian S. Decreasing and fast solutions for a second-order difference equation related to Fisher-Kolmogorov’s equation［J］.Journal of Mathematical Analysis and Applications，2010，363(1):97-110.

［9］Noomen Khiari，Khaled Omrani. Finite difference discretization of the extended Fisher-Kolmogorov equation in two dimensions［J］.Computers and Mathematics with Applications，2011(62):4151-4160.

［10］Tlili Kadri，Khaled Omranib. A second-order accurate difference scheme for an extended Fisher-Kolmogorov equation［J］.Computers and Mathematics with Applications，2011(61):451-459.

［11］Macías-Díaz J E.A bounded numerical method for approximating a hyperbolic and convective generalization of Fisher’s model with nonlinear damping［J］.Applied Mathematics Letters，2012(25):946-951.

［12］SUN Zhizhong.On the compact difference scheme for heat equation with Neumann boundary conditions［J］. Numer Methods Partial Differ Equ，2009(25):1320-1341.

［13］LI Juan，SUN Zhizhong，ZHAO Xuan. A three level linearized compact difference scheme for the Cahn-Hilliard equation［J］.Science China Mathematics，2012，55(4):805-826.