非局域耦合帐篷映像中的完全同步周期态

杨科利，屈世显

（1陕西师范大学 物理学与信息技术学院，陕西 西安710119；2宝鸡文理学院 物理与光电技术学院，陕西 宝鸡721016）

同步是一种非常普遍存在的自然现象，它是指 两个和多个系统通过某种耦合导致其动力系统状态趋于一致的现象，该现象在许多实际过程中发挥着非常重要的作用。然而，相关的耦合系统同步研究都是基于连续（时间和空间）动力学系统，对于不连续动力学系统的讨论相对较少。研究发现仅仅是时间不连续的动力学系统，其同步过程要远远比连续时间系统复杂。事实上，实际系统动力学常常表现出不连续性，其中一个简单的例子就是分段线性系统，如：神经元分段线性模型［1］、细胞中动力学［2］、神经网络［3］、张弛振荡［4］、蔡氏电路［5］、干摩擦、冲击振子［6］、弹跳球［7］、齿轮等。近年来人们在分段线性系统中发现了许多不同于连续系统的奇特现象［8－12］。随着分段线性系统中各种新现象的发现，耦合分段线性系统的研究也得到了研究者的关注，特别是此系统中同步现象的研究也引起了人们的注意。Cencini等［13］研究发现，耦合分段线性系统的同步转换具有不连续性，在低维耦合系统中可以找出一个系统同步临界耦合强度，但对于高维系统，由于系统的分段线性特征，很难找到确定的临界耦合强度。这说明耦合分段线性系统中的动力学特性有别于耦合连续系统，因此有必要对耦合分段线性系统做深入的研究。

在较简单的耦合方式当中，非局域耦合是更贴近实际系统的一种相互作用方式，如神经科学和电化学系统等。最近，我们研究了全局耦合和紧邻耦合的分段线性系统的完全同步态［14－15］，发现了一些有别于连续系统的新特性。在非局域耦合方式下，人们发现了网络中的奇异态现象［16］。本文着重研究非局域耦合下分段线性系统的动力学行为，分析非局域耦合分段线性系统的周期态以及完全同步周期态。由于分段线性系统更贴近于实际系统，所得到的结果将有助于理解现实生活网络中出现的一些节律现象。对于非局域耦合分段线性系统中周期态的研究将有助于解释大脑神经的一些现象和功能，特别是大脑中神经元放电时形成的奇异态、神经集体放电导致癫痫疾病以及学习和记忆功能。

1 模型

含有N个节点的非局域耦合系统的动力学行为满足下述方程：

其中xn（i）是系统中第i个节点在n时刻的动力学变量，系统尺寸为N，ε是节点间的耦合强度，采用周期边界条件xn（i）＝xn（i＋N），P是与第i个节点相连接的两边近邻节点的个数，即耦合半径；f（x）是一维分段线性映像。为了简单起见，我们选取如下分段线性映像：

固定μ＝2，此时映像变为满帐篷映像，系统的李雅普诺夫指数λ＝ln 2＞0，系统呈现混沌状态，并且有两个平庸不动点x＊1＝0，x＊2＝2／3。由于映像的两个分支的斜率的绝对值都为2，此时映像的拉伸和折叠行为一致，所以系统存在不稳定周期轨道。而且当初值为无理数时，系统将呈现非周期态。

2 结果和分析

采用信息熵H［17］来度量非局域耦合分段线性系统中可能的周期态，由于采用耗散耦合形式，耦合系统每一个节点的状态xn（i）仍然分布在［0，1］区间上。为此，将区间［0，1］等分成512份，统计第i个节点的状态值落在第m个区间的概率pmi，相应的耦合系统信息熵的定义为

在计算过程中，随机选取一套初值，首先丢掉50 000次暂态，之后使用接下来的50 000次迭代中的态，并统计第i个节点的状态值落入第m个区间的概率pmi，且对50 000次迭代取平均。需要注意的是，信息熵H最终对空间取了平均，因此与单个节点的熵基本上没有差别。从时间尺度来说，耦合系统只有两种状态：周期和混沌。当系统处于混沌态时，pmi＝1／512，对应的信息熵H ＝9；当系统全部处于不动点时，pmi＝1，此时系统对应的信息熵H ＝0；当系统处于同步的周期态时，信息熵为0≤H＜9。因此信息熵H越小表示系统最有可能处于周期态。通过此信息熵H，即可区分系统的这两种状态。图1a给出了系统在耦合半径P和耦合强度ε两个参数下信息熵的分布，黑色表示低信息熵，此时系统处于周期态，白色表示高信息熵，此时系统处于混沌态。由图中可以看出，大致有四个区域出现了黑色的点，说明在这些参数下系统将呈现多种周期态，周期态的具体样式我们将在下面详细讨论。

为了讨论系统的周期态的同步性质，引入同步序参量［18］来刻画系统的同步，其定义为

其中Rn和φn分别表示n时刻的振幅和相位，如果系统的每个状态都完全相同，即：xn（1）＝xn（2）＝…＝xn（N），则Rn＝1。计算系统在耦合半径P和耦合强度ε两个参数下系统同步序参量的分布，如图1b所示，白色代表同步序参量Rn＝1，系统处于同步态，由白色到黑色，系统的同步程度逐渐减弱。当耦合半径达到一定程度时，系统随着耦合强度的增大，所有节点的动力学趋于同步。由于非局域耦合也是一种规则的耦合方式，连接矩阵的本征值可以解析求解，因此系统从混沌同步到混沌非同步的临界点可以解析得到（见图1b中的黑色实线），即Blowout分岔线：

图1 非局域耦合帐篷映像的相图Fig.1 Phase Diagram for the nonlocal coupled tent maps其中：信息熵H分布图中黑色表示低信息熵，系统处于周期态；白色表示高信息熵，系统处于混沌态。同步序参量R分布图中白色代表同步序参量R＝1，系统处于同步态，由白色到黑色，系统的同步程度逐渐减弱。

其中P为耦合半径，λu为单映像的李雅普诺夫指数，N为系统的节点数，εc是系统要达到同步所需要的最小耦合强度，即临界耦合强度（见图1中的黑色实线），该曲线右侧为完全同步周期态，左侧为非同步态。

对比图1a和1b，可以发现系统信息熵较小的4个区域可以分成两类：一类是非同步周期态，另一类是完全同步周期态。首先，分析非同步周期态的特征。分别在图1a中选取4个点，绘制耦合系统的空间振幅图，结果如图2所示。图2a对应图1a中的A点，即ε＝0.9，P＝64时的状态；图2b对应图1a中的B点，即ε＝0.9，P＝31时系统的状态；图2c对应图1a中的C点，即ε＝0.9，P＝20时系统的状态；图2d对应图1a中的D点，即ε＝0.9，P＝58时系统的状态。由图2可以看出，系统的状态在这些参数下表现出空间连续分布的波形状，且在给定耦合强度下，波峰的个数随耦合半径的减小而增加。例如：图2a中只有一个波峰，图2b中有两个波峰，图2c中有三个波峰，且系统都处于周期2状态，这三种情形刚好对应于图1a中非同步周期态的三个条状区域。仔细观察图1a中的A点左侧D点附近仍然有一很窄的信息熵H较小的灰色区，与D点相应的空间振幅图2d对比，发现该图仍然显示波状空间振幅空间分布，但是却在时间尺度上呈现周期4状态。

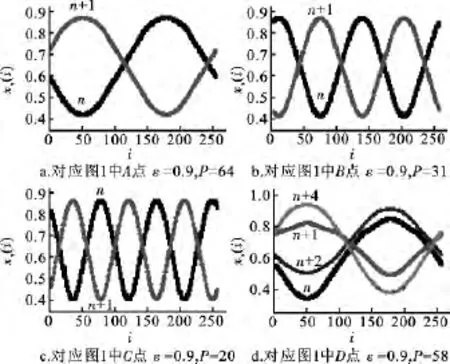
图2 非同步下系统周期态的空间振幅图Fig.2 The space－time plot of the nonlocal coupled system

上述分析显示，耦合系统的非同步状态总是以格点动力学状态在空间的周期性连续分布为特征，且在时间上也呈现周期态。其空间周期随耦合半径的减小而减小，而时间周期也依赖于耦合半径。在图1中同一条状区域里还存在其他较窄的周期区域，这些区域呈现出较高的周期态。这些结果与近年来在耦合Logistic映像和耦合光偏振实验结果［19］相一致，其应该是非局域耦合离散系统共有的属性。此外，本文更加关心耦合系统中完全同步周期态的特征。

本研究发现了非局域耦合分段线性系统中一些很特别的同步周期态。注意图1a右上角的黑色区域，其中黑色的点对应系统的信息熵H＝0时的状态参数。在这些参数下系统完全同步到x＊1＝0的不动点，这是平庸的完全同步态，不是本文关注的重点。而与该区域中浅灰色点相对应的参数下系统的动力学则是我们感兴趣的问题，因为在这些参数下耦合系统呈现出一些特殊的完全同步周期态。在图1a右上角选取E和F两个点，绘制耦合系统的时空演化图和节点动力学状态的时间序列（如图3所示），其中图3a和3b对应图1a中的E点，即ε＝0.87，P＝114时的状态，而图3c和3d则对应图1a中的F点，即ε＝0.81，P＝89时的状态。由图3可见，在上述两套参数下耦合系统达到完全同步，且呈现出周期均为53的严格周期运动状态。有趣的是，在图3b中发现系统同步状态在空间中呈现具有规则周期的脉冲，而图3d显示，在与图3b中任意两相继的脉冲之间又出现另一规则脉冲。

图3 同步下系统周期态的时空振幅演化图和系统中节点动力学状态的时间序列Fig.3 The space－time plot of complete periodic synchronous states

上述现象与以往观察到的耦合映像系统中通常的同步现象有显著区别。一般而言，当耦合系统达到同步态时，系统中各个格点的动力学状态都同步到单个映像的稳定周期轨道或混沌轨道。而本文所涉及的映像是一个满帐篷映像，系统处于混沌状态，仅存在两类轨道，即可数无穷多不稳定周期轨道和不可数无穷多非周期轨道。对于［0，1］区间的任意初值，得到非周期轨道的概率为1，而得到周期轨道的概率为0。即使精确地将初值取在一个周期点上，舍入误差也将使这条轨道或迟或早地落入非周期轨道。因此满映像的典型轨道都是非周期的［20］。显然这里的同步周期态不是单个映像的稳定周期轨道。在本文研究的系统中格点间动力学的耦合很可能造成系统同步于单映像的某些不稳定周期轨道。时间序列图3b和3d中的脉冲状变化是由于同步轨道中存在接近于峰值的周期点，在峰值以前迭代点渐进累计到达峰值附近，并且在峰值附件发生折叠，使其动力学状态再次投射到最左端的不稳定不动点x＊＝0附近，继续其周期运动。

按照符号动力学的语言，图3b和3d所对应的周期轨道序列分别为LnR和LnRLmR，其中L和R分别表示轨道点在映像峰值的左侧和右侧迭代，n和m表示其在峰值左侧的迭代次数。该两类轨道的周期分别为n＋1和m＋n＋2。对于图3b的情况，n＝52，由迭代映像（2）可得其不动点方程为

对于图3d的情况，n＝18，m＝33，不动点方程为

将n＝52带入（6）式，得到起始周期点x0＝x＊＝2.220 446 049 250×10－16。将n＝18，m＝33代入（7）式，得到起始周期点x0＝x＊＝3.814 697 265 403×10－6。分别以上述两个初值为起点，根据单映像（2）迭代得到两个非稳定周期点的时间序列。将其分别与图3b和3d中两个同步周期轨道的时间序列比较发现，其精确符合。至此可以证明：图3中的两种同步周期轨道就是单映像的非稳定周期轨道，正是由于格点动力学间的非局域耦合造成了系统的同步动力学稳定在单映像的非稳定周期轨道。事实上，上述两类周期序列的不同组合可以造成比图3所示脉冲序列更丰富的行为。该现象表明，可以用这类不连续的分段线性映像模拟神经元的累积放点现象，用耦合分段线性映像模拟神经元间突触电耦合所产生的丰富放电行为。

3 结论

本文用数值模拟的方法研究了非局域耦合帐篷映像中的周期态，分别采用耦合系统的信息熵和同步序参量刻画耦合系统的动力学行为。研究结果表明，在非局域耦合帐篷映像系统中存在两类周期态：一类是非同步周期态，另一类是完全同步周期态。在参数空间的3个条状区域存在非同步周期态，其在空间上呈连续的波峰型分布，在时间上也呈现周期状态。随着耦合强度和耦合半径的变化，其在空间周期和时间周期也会随之变化。所发现的完全同步周期态具有特殊性，它是由耦合系统中格点动力学耦合所造成。在这类同步态中，系统格点的动力学同步于单映像的非稳定周期轨道，不同于以往在非局域耦合系统中所观察到的同步态，可以用来模拟耦合神经元的丰富放电行为。

［1］Ibarz B，Casado J M，Sanjua＇n M A F.Map－based models in neuronal dynamics［J］.Physics Reports，2011，501（1）：1－74.

［2］Tyson J J，Chen K C，Novak B.Sniffers，buzzers，toggles and blinkers：Dynamics of regulatory and signaling pathways in the cell［J］.Current Opinion in Cell Biology，2003，15（2）：221－231.

［3］Liu Q，Wang J.A one－layer recurrent neural network with a discontinuous hard－limiting activation function for quadratic programming［J］.IEEE Transactions on Neural Networks，2008，19（4）：558－570.

［4］Hahn H S，Nitzan A，Ortoleva P，et al.Threshold excitations，relaxation oscillations，and effect of noise in an enzyme reaction［J］.Proceedings of the National A－cademy of Sciences，1974，71（10）：4067－4071.

［5］Heslot F，Baumberger T，Perrin B，et al.Creep，stickslip，and dry－friction dynamics：Experiments and a heuristic model［J］.Physical Review E，1994，49（6）：4973－4988.

［6］Nordmark A B.Non－periodic motion caused by grazing incidence in an impact oscillator［J］.Journal of Sound and Vibration，1991，145（2）：279－297.

［7］Mehta A，Luck J M.Novel temporal behavior of a nonlinear dynamical system：The completely inelastic bouncing ball［J］.Physical Review Letters，1990，65（4）：393－396.

［8］Qu S X，Wu S，He D R.Multiple devil′s staircase and type－V intermittency［J］.Physical Review E，1998，57（1）：402－411.

［9］Qu S X，Wu S，He D R.A multiple devil′s staircase in a discontinuous map［J］.Physics Letters A，1997，231（3）：152－158.

［10］He D R，Wang B H，Bauer M，et al.Interaction between discontinuity and non－invertibility in a relaxation oscillator［J］.Physica D，1994，79（2）：335－347.

［11］屈世显，Christiansen B，何大韧.一个不连续不可逆映象中的新型激发［J］.物理学报，1995，44（6）：841－852.

［12］Qu Shixian，Lu Yongzhi，Zhang Lin，et al.Discontinuous bifurcation and coexistence of attractors in a piecewise linear map with a gap［J］.Chinese Physics，2008，17（12）：4418－4423.

［13］Cencini M，Tessone C J，Torcini A.Chaotic synchronizations of spatially extended systems as nonequilibrium phase transitions［J］.Chaos，2008，18（3）：037125.

［14］Yang Keli，Chen Huiyun，Du Weiwei，et al.Partial and complete periodic synchronization in coupled discontinuous map lattices［J］.Chinese Physics B，2014，23：070508.

［15］程兴超，杨科利，屈世显.一个全局耦合不连续映像格子中的奇异态［J］.物理学报，2014，63（14）：140505.

［16］Sethia G C，Sen A.Chimera states：The existence criteria revisited［J］.Physical Review Letters，2014，112（14）：144101.

［17］Hagerstrom A M，Murphy T E，Roy R，et al.Experimental observation of chimeras in coupled－map lattices［J］.Nature Physics，2012，8（9）：658－661.

［18］Kuramoto Y，Nishikawa I.Statistical macrodynamics of large dynamical systems：Case of a phase transition in oscillator communities［J］.Journal of Statistical Physics，1987，49（3／4）：569－605.

［19］Hagerstrom A M，Murphy T E，Roy R，et al.Experimental observation of chimeras in coupled－map lattices［J］.Nature Physics，2012，8（9）：658－661.

［20］郝柏林.从抛物线谈起—混沌动力学引论［M］.2版.北京：北京大学出版社，2013.