基于F类函数一种新的二元Copula构造
闫晓丽,何小娟,段永超
(太原科技大学应用科学学院,太原 030024)
基于F类函数一种新的二元Copula构造
闫晓丽,何小娟,段永超
(太原科技大学应用科学学院,太原 030024)
介绍了二元Copula函数定义和Sklar定理,提出了基于F类函数一种新的二元Copula构造形式,并对这种二元Copula函数的性质进行推导和研究。Copula函数的实际应用极为广泛,这种新的二元Copula函数可以扩大函数模型的选择范围,有利于我们选择恰当的Copula函数模型来解决实际问题。
F类函数;二元Copula函数;构造形式
Copula函数作为研究变量相关性的工具,不仅克服了传统相关性分析方法研究变量非线性、非对称的不足,而且能够更加全面完整地刻画变量间的结构。Copula函数作为一种连接函数可以将联合分布的构造问题拆分为边缘分布和它们之间的相关结构来研究,而且在随机变量作单调变换后仍会保持变量间的相关性不变,此外它还可以捕捉到变量间的尾部相关性等特性。因此,Copula函数常被应用到保险精算、风险管理,股票分析等领域用于变量间的相关性分析,并取得良好效果。然而在实际应用中,针对不同的问题需要不同的Copula函数去求解,没有一个通用的构造方法,因此极大制约了Copula函数在实际中的应用,所以构造适当可行的Copula函数是当今的研究热点。目前,针对二元Copula的构造方法有许多种:如Sklar定理反演法[1],可以直接从二元联合分布函数求得二元Copula函数;Copula函数的任意线性凸组合[1]也可以构造Copula函数;单调变换法[2],在非参数统计中,由于随机变量在严格单调变换下的Copula要么不变,要么以某种规律发生变化,所以可通过单调变换来构造Copula函数;基于g函数[3]的二元Copula函数以及构造阿基米德Copula生成元[4]等多种构造方法。目前Copula函数族主要分为两大类:椭圆族Copula和阿基米德族Copula,其中阿基米德族Copula具有对称性、可结合性等特点,所以是应用较为广泛的一类Copula函数,对于这类函数只要找到满足特定条件的生成元就能构造Copula函数。
F类函数[5]也相当于一种阿基米德生成元,本文在已有的F类函数的基础上,提出了一种新的二元Copula函数的构造形式,并研究了新的二元Copula函数的三种性质。
1 二元Copula函数
1.1 二元Copula函数定义
一个二元函数是Copula函数(I2→I(I=[0,1])),若满足以下条件:
(1)边界:∀u,v∈I,C(0,v)=C(u,0)=0,C(1,v)=v,C(u,1)=u.
(2)增性:对于∀a,b,c,d∈I,且a≤b,c≤d,有:
Vc([a,b]×[c,d])=C(b,d)-C(a,d)-C(b,c)+C(a,c)≥0
Vc([a,b]×[c,d])为Copula在矩形[a,b]×[c,d]上的二阶差分。
1.2 Sklar定理
Sklar定理是Copula理论中的基础定理,定理如下:
Sklar定理:假设二维随机变量(X,Y)的联合分布为H,边缘分布为F和G,则存在着一个Copula函数C,使得:
H(x,y)=C(F(x),G(y))
若F和G是连续的,则Copula函数是唯一的;否则,在RanF×RanF上Copula函数是唯一的。
Frechet-Hoeffding给出了联合分布函数的上下界。若H是联合分布,边际分布是F和G,则:
max{F(x)+G(y)-1,0}≤H(x,y)≤min{F(x),G(y)}
因为H(x,y)=C(F(x),G(y))所以上式可以等价为:
W(u,v)=max{u+v-1,0}≤C(u,v)≤min{u,v}=M(u,v)
2 新的二元Copula函数构造
2.1 F类函数
F类函数满足的条件如下:f(x)是递增凹函数(f′(x)≥0,f″(x)≤0)
(1)f(0)=0,f(1)=1
(2)f′(x)+xf″(x)≤0,x∈[0,1]
2.2 新的二元Copula函数
本文构造的二元Copula函数是以F类函数为基础提出的,函数形式如下:
C(u,v)=uv+f(u)f(v)-f(uv)
下面证明这种新的构造形式确为二元Copula函数。
首先证明构造出的新的函数形式满足二元Copula函数条件:
(1)边界:C(1,v)=v+f(1)f(v)-f(v)=v+f(v)-f(v)=v,
C(u,1)=u+f(u)f(1)-f(u)=u+f(u)-f(u)=u,
C(0,v)=0+f(0)f(v)-f(0)=0,C(u,0)=0+f(u)f(0)-f(0)=0.
(2)增性:u1,u2,v1,v2∈I,且u1 因为u2>u1,v2>v1,且f(x)在I上单调递增,所以: (u2-u1)(v2-v1)+(f(u2)-f(u1))(f(v2)-f(v1))≥0 令:g=f(u2v1)+f(u1v2)-f(u2v2)-f(u1v1)=(f(u1v2)-f(u1v1))-(f(u2v2)-f(u2v1)) 再令:h(x)=f(v2x)-f(v1x),得:g=h(u1)-h(u2), 若w(x,y)=yf′(yx),则h′(x)=v2f′(v2x)-v1f′(v1x)=w(x,v2)-w(x,v1), wy(x,y)=∂yf′(yx)/∂y=f′(yx)+xyf″(yx). 由条件f′(x)+xf″(x)≤0,x∈[0,1]. 可知wy(x,y)≤0. 因为v1 所以对u1 因此,对u1 满足二维递增性,所以C(u,v)=uv+f(u)f(v)-f(uv)为二维Copula函数。 2.3 新二元Copula函数性质 (2)∀u1,u2,v1,v2∈I,且u1 Vc([u1,u2]×[v1,v2])=C(u2,v2)-C(u2,v1)-C(u1,v2)+C(u1,v1)= 证明:(1)首先证明f2(t)=f1(λt)/f1(λ)是F类函数。 f2(0)=f1(0)/f1(λ)=0,f2(1)=f1(λ)/f1(λ)=1. (2) 证明新构造的C(u,v)确为二元Copula函数,满足二元Copula函数的条件: 边界:C(u,0)=C(0,v)=0, 增性:u1,u2,v1,v2∈[0,1],u1 Vc([u1,u2]×[v1,v2])=C(u2,v2)-C(u1,v2)-C(u2,v2)+C(u1,v1)=u2v2+f2(u2)f2(v2)-f2(u2v2)-u2v1-f2(u2)f2(v1)+f2(u2v1)-u1v2-f2(u1)f2(v2)+f2(u1v2)+u1v1+f2(u1)f2(v1)-f2(u1v1)=(u2-u1)(v2-v1)+(f2(u2)-f2(u1))(f2(v2)-f2(v1))-f2(u2v2)+f2(u2v1)+f2(u1v2)-f2(u1v1) (u2-u1)(v2-v1)+(f2(u2)-f2(u1))(f2(v2)-f2(v1))≥0 g=f2(u2v1)+f2(u1v2)-f2(u2v2)-f2(u1v1)=(f2(u1v2)-f2(u1v1))-(f2(u2v2)-f2(u2v1)) 可知wy(x,y)≤0. 因为v1 所以对∀u1 则Vc([u1,u2]×[v1,v2])=C(u2,v2)-C(u1,v2)-C(u2,v2)+C(u1,v1)≥0. 性质3 设f1(t),f2(t)是F类函数,则g(t)=f2(f1(t))为F类函数,且构造的C(u,v)=uv+f2(f1(u))f2(f1(v))-f2(f1(uv))是二元Copula函数。 证明:(1)证明g(t)=f2(f1(t))是F类函数。 g(0)=f2(f1(0))=0,g(1)=f2(f1(1))=1. 所以g(t)也是F类函数。 (2)证明新构造C(u,v)确为二元Copula函数,满足二元Copula函数条件: 边界:C(u,0)=0+f2(f1(u))f2(f1(0))-f2(f1(0))=0. C(0,v)=0+f2(f1(0))f2(f1(v))-f2(f1(0))=0. 增性:∀u1,u2,v1,v2,u1 Vc([u1,u2]×[v1,v2])=C(u2,v2)-C(u2,v1)-C(u1,v2)+C(u1,v1)=u2v2+g(u2)g(v2)-g(u2v2)-u2v1-g(u2)g(v1)+g(u2v1)-u1v2-g(u1)g(v2)+g(u1v2)+u1v1+g(u1)g(v1)-g(u1v1)=(u2-u1)(v2-v1)+(g(u2)-g(u1))(g(v2)-g(v1))+g(u1v2)+g(u2v1)-g(u2v2)-g(u1v1) 所以(u2-u1)(v2-v1)+(g(u2)-g(u1))(g(v2)-g(v1))≥0. 令:H=g(u2v1)+g(u1v2)-g(u2v2)-g(u1v1)=(g(u1v2)-g(u1v1))-(g(u2v2)-g(u2v1)). h(x)=g(v2x)-g(v1x),w(x,y)=yg′(yx), 所以H=h(u1)-h(u2). h′(x)=v2g′(v2x)-v1g′(v1x)=w(x,v2)-w(x,v1) wy(x,y)=∂yg′(yx)/∂y=g′(yx)+xyg″(yx). 由已知g′(t)+tg″(t)≤0,可得wy(x,y)≤0,所以h′(x)<0,h(x)单调递减,所以H≥0,则Vc([u1,u2]×(v1,v2))=C(u2,v2)-C(u1,v2)-C(u2,v2)+C(u1,v1)≥0. 因此构造C(u,v)=uv+g(u)g(v)-g(uv)=uv+f2(f1(u))f2(f1(v))-f2(f1(uv)). 是一个二元Copula函数。 本文在已有的F类函数的基础上,提出了一种新的二元Copula函数的构造形式,并研究了新的二元Copula函数三种性质,证明这种新的构造形式确实合理可行。对于这种新的二元Copula函数在实际中的应用将是以后的研究热点。 [1]NELSONRB.AnIntroductiontoCopula[M].NewYork:Springer-Verlga,1999. [2] 李霞,张明珠.随机变量之间相依性的有关研究[J].西南民族大学学报,2005,31(3):356-358. [3] 曾霞,王沁.一种构造阿基米德生成元的方法[J].浙江大学学报,2011,38(4):391-394. [4] 陈崇双.阿基米德生成元的复合构造研究[J].西南民族大学学报,2008,34(6):1145-1151. [5] 徐艳兰,王传玉.基于类函数的二元的构造[C]∥第四届中国智能计算大会,北京,2010:234-239. [6] 刘洁,王丽芳.混合优化算法预测股票价格[J].太原科技大学学报,2014,35(3):194-197. [7] 王高雄,周之铭,王寿松.常微分方程[M].北京:高等教育出版社,2005. [8] 程玉林,张小磊.一类二元对称的函数[J].应用数学,2008,20:48-51. A New Construction Method of 2-Copula Based on F-Function YAN Xiao-Li,HE Xiao-Juan,DUAN Yong-Chao (School of Applied Science,Taiyuan University of Science and Technology,Taiyuan 030024,China) This paper introduces the definition of 2-Copula and the Sklar theorem,puts forward a new method to construct 2-Copula based on F-function.Furthermore,the properties of this new Copula function are analyzed. This Copula function has wide practical application and can expand the range of chance for function model,which helps choose the appropriate Copula function model so as to solve actual problems. F-function,2-Copula,construction methods 2015-03-20 校博士启动基金(20122026);2013省级UIT项目(2013244) 闫晓丽(1990-),女,硕士研究生,主要研究方向为最优化理论及其应用。 1673-2057(2015)06-0486-05 0221 A 10.3969/j.issn.1673-2057.2015.06.015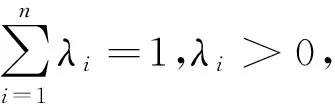
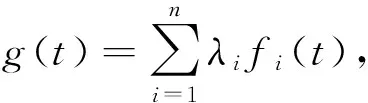
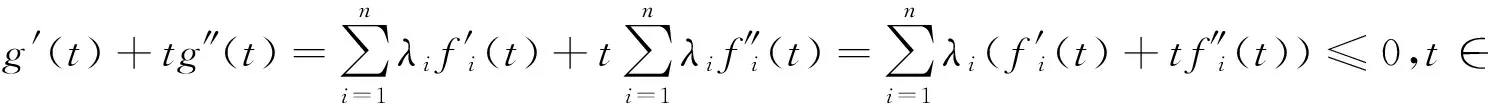
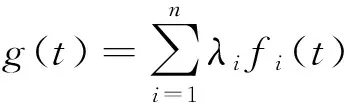
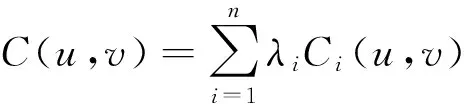
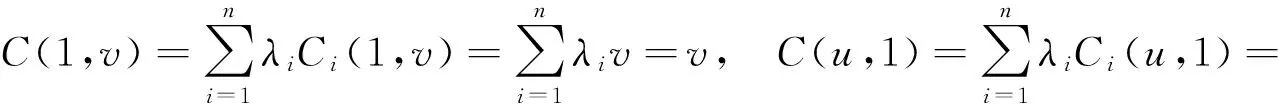
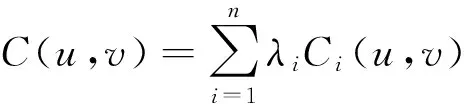
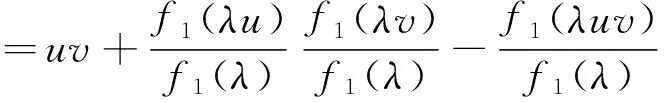
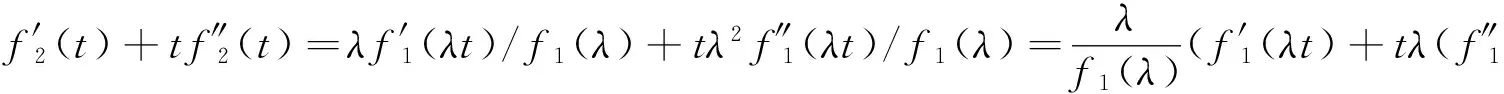
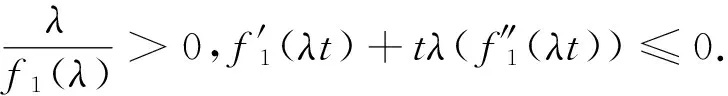
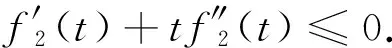
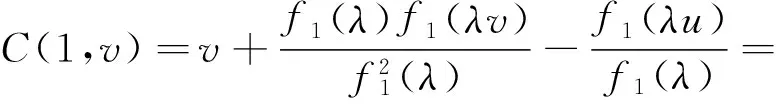

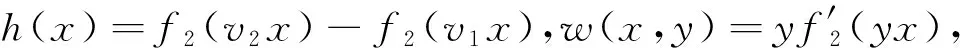
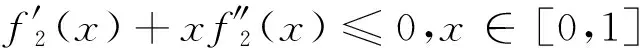
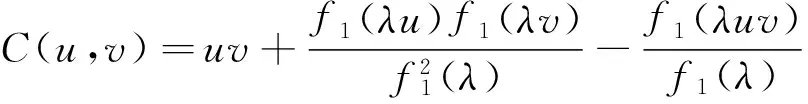
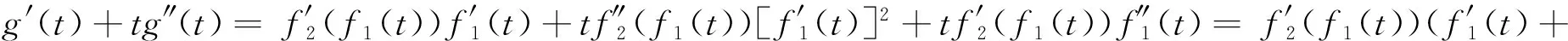
3 结束语

