用微分求积法分析轴向移动粘弹性梁的非平面非线性振动*

王冬梅 张伟 李慕荣

（1.北京工业大学机电学院，北京 100124）（2.济宁学院数学系，曲阜 273155）（3.济宁金桥煤矿，济宁 272200）

引言

轴向移动粘弹性梁可以作为多种工程装置的力学模型，比如动力传送带、磁带、带锯、空中缆车索道、高楼升降机缆道、单索架索道等.轴向移动粘弹性梁的非线性动力学性质对工程装置的稳定性和可靠性有着重要的影响.因此分析轴向移动粘弹性梁的非线性振动的非线性动力学行为对分析解决工程的实际问题有着重要的意义.中外学者采用各种近似方法对此作了大量工作.2000年，Öz［1］等用直接多尺度法研究了刚度较小、速度有微小扰动情况下的轴向运动梁.2002年Marynoeski和Kapitaniak［2］采用 Galerkin方法，分析了 Kelvin和 Burgers两种粘弹性模型下轴向运动梁的动态特性.2005年和 2006年，杨晓东和陈立群［3-4］采用Galerkin方法对轴向移动梁的动力学特性比如共振稳定性、分叉和混沌等做了大量的研究，取得了许多有意义的成果.2009年，丁虎和陈立群［5］分别用微分求积法和有限差分法对轴向移动梁的两种非线性横向振动模型进行了分析比较.以上文献都是对轴向移动梁的横向平面振动进行的研究，对其非平面非线性振动的研究还很少.2010年，陈丽华等［6］用3阶伽辽金截断研究了轴向移动梁面内和面外耦合的非线性振动，讨论了轴向加速度的振幅、频率对其长时间动力学行为分叉、混沌的影响.2013年，Ghayesh和 Amabili［7］利用 Galerkin方法研究了轴向移动铁木辛哥梁三维非线性平面振动的非线性动力学行为.

国内外学者大都采用Galerkin方法研究轴向移动梁的非线性动力学特性，很少有学者用微分求积法对轴向移动梁的非线性动力学性质进行分析.用微分求积法来分析轴向移动梁非平面非线性振动的研究还未见报道.微分求积法相比于Galerkin方法原理简单（不依赖变分原理），计算量小，对非线性动力学方程可以直接求解，减少了Galerkin方法寻找模态函数的麻烦.另外，Galerkin方法处理问题时仅提取有限的低阶振型作近似处理，Galerkin方程的形成，需要积分，当阶数较高时，非线性项的显式表达式很难求出；而微分求积法则克服了这种局限性，本质上考虑了所有振型的综合贡献.

本文利用微分求积法对轴向移动梁横向非平面非线性振动的复杂动力学特性（分叉、混沌、周期等）进行分析.

1 控制方程组

陈丽华等人［6］利用哈密顿原理建立的轴向移动粘弹性梁横向非平面非线性振动的动力学控制方程为如下非线性偏微分方程组：

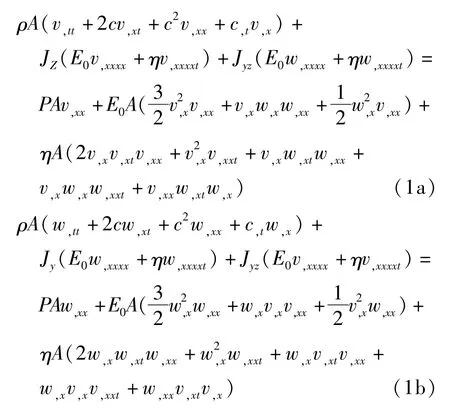
边界条件：

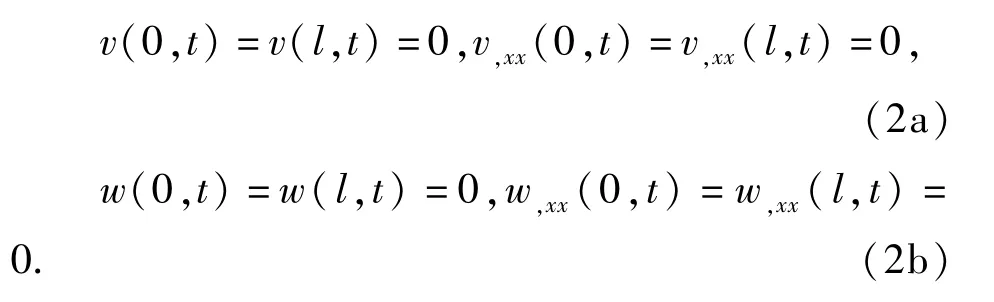
其中，ρ为密度，A是截面积，l是梁的长度，v（x，t），w（x，t）分别表示轴向移动梁面内和面外横向振动的位移，η是粘弹系数，E是杨氏模量，Jy，Jz和Jyz是惯性力矩.假定在预紧力P0处有一小的扰动P1sinωt，也就是说紧力 P＝P0+P1sinωt；假定轴向运动的速度是简谐变化的，也就是c＝c0+c1sinωt.这种假设是有它的物理意义的.比如，当我们用轴向移动梁来模拟一对转动轮上的带时，轮子转动时的扰动，会引起带轴向移动速度的扰动.

2 微分求积法求解控制方程

微分求积法的基本原理是将函数在求解区域内的每个网格点处的导数值用域内全部网格点上的函数值的加权线性和近似表示.关于微分求积法的理论在文献［9］中有详细的论述，包括权系数的计算、节点的选取、边界条件的处理等.

依照微分求积法原理，引入N个网格点：

方程（1）中未知函数对空间变量的各阶偏微分在各网格点处的值可以表示为

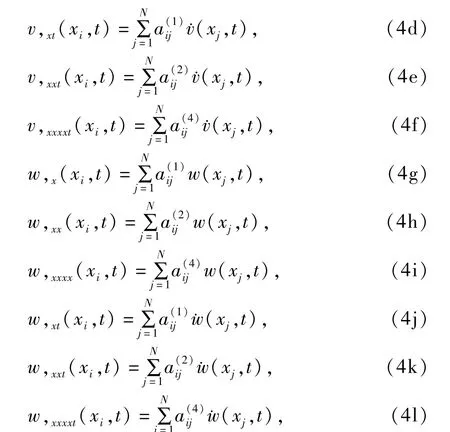
其中分别是微分求积法中一阶导数、二阶导数、四阶导数的权系数，其计算公式见文献［8］，v，x（xi，t）v，xx（xi，t），v，xxxx（xi，t），w，x（xi，t），w，xx（xi，t），w，xxxx（xi，t）分别表示函数 v（x，t），w（x，t）在各节点处关于空间变量x一阶、二阶、四阶偏导数，˙v（xi，t），˙w（xi，t）分别表示函数 v（x，t），w（x，t）在各节点处对时间t的一阶导数.因系统（1）的边界条件是简支边界条件，可用权系数矩阵修正法［8］处理该边界条件.处理边界条件后，将（4）代入控制方程（1）得，

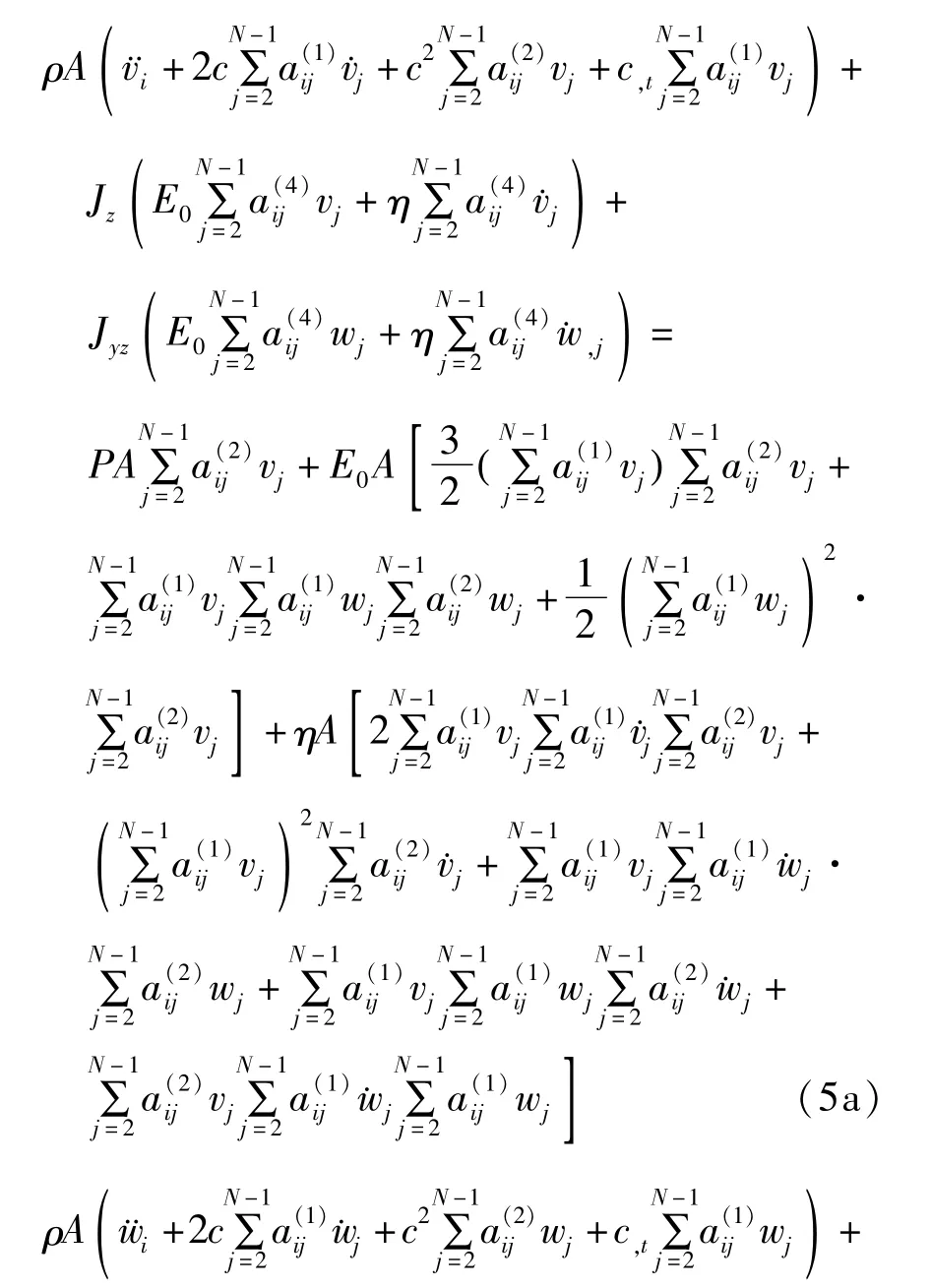
其中 vj＝v（xj，t），wj＝w（xj，t），（j＝2，3，…，N-1）.方程（5）是以2×（N-2）个轴向移动粘弹性梁面内和面外振动的位移（v2，v3，…，vN-1），（w2，w3，…，wN-1）为未知变量的非线性常微分方程组.给定初始条件和参数，求解常微分方程组（5）既得轴向移动粘弹性梁横向非平面非线性振动的动力学响应.

3 轴向移动梁非平面振动的动力学性质

给定初始条件和参数 v（x，0）＝0，vt（x，0）＝0.01，w（x，0）＝0，wt（x，0）＝0.01，ρ＝1000kg／m3，A＝1×10-4m2，l＝1.0m，Jy＝＝0，ω＝15HZ，E＝1.5×108N／m2，η＝4.0×105Ns／m2，P0＝P1＝100N，对常微分方程组（5）进行求解，在数值结果的基础上利用分叉图、相图、时间历程图对轴向移动粘弹性梁横向非平面非线性振动的动力学行为进行分析.分别考虑了轴向运动定常速度、轴向运动速度变化幅值对其动力学行为的影响.

3.1 轴向运动定常速度的影响

取轴向运动速度变化幅值c1＝2.1m／s，作出面内和面外振动的位移v和w随轴向运动定常速度c0在区间15，[]25 m／s上变化时的分叉图如图1.从分叉图1我们可以看出在c0由15m／s变化到大约21.9 m／s时，面内运动和面外运动都是混沌运动.随着c0的增加，出现了一个小的周期窗口，即面内运动和面外运动都由混沌运动变为周期运动.大约增大到23.1m／s时，二者运动又都变为混沌运动了.当c0继续增大到24m／s时，二者运动又变为周期的了.

图1 轴向运动定常速度的影响（a）位移v随c0变化的分叉图；（b）位移w随c0变化的分叉图Fig.1 Effect ofmean axial velocity（a）bifurcation diagrams for the displacement v via c0；（b）bifurcation diagrams for the displacement w via c0

3.2 轴向运动速度变化幅值的影响

图2 轴向运动速度变化幅值的影响（a）位移v随c1变化的分叉图；（b）位移w随 c1变化的分叉图Fig.2 Effect of amplitude of axial velocity fluctuation（a）bifurcation diagrams for the displacement v via c1；（b）bifurcation diagrams for the displacement w via c1

取轴向运动定常速度c0＝20.5m／s，作出面内和面外振动的位移v和w随轴向运动速度变化幅值 c1在区间 [0 .5，3.5] m／s上变化时的分叉图如图2.从分叉图2我们可以看出在c1由0.5m／s变化到大约1.4m／s时，面内运动呈2倍周期运动，面外运动呈单倍周期运动.面内运动由单倍周期运动变化为2倍周期运动.随着c1的增大，面内运动和面外运动都由周期运动变化为混沌运动.当c1增大到1.5m／s时，混沌运动消失，面内和面外运动变为多倍周期运动.很快，二者运动又进入混沌状态直到最后.

图1和图2都表明，在相同参数下，面内运动和面外运动的动力学性质始终保持一致，即二者同时进入周期运动或混沌运动.下面图3～图5是一些典型的周期运动和混沌运动的相图，时间历程图.其中（a）是以面外运动速度、面外运动位移以及面内运动的位移为横、纵、竖坐标的三维相图，（b）和（c）分别是以面内运动的速度、位移，面外运动的速度、位移为横纵坐标的平面相图.（d）和（e）分别表示面内运动位移和面外运动位移随时间变化的波形图.从这些图形中可以看出，在相同参数下，无论是从相图，还是时间历程图所得的轴向移动梁横向非平面振动的动力学性质是相同的.

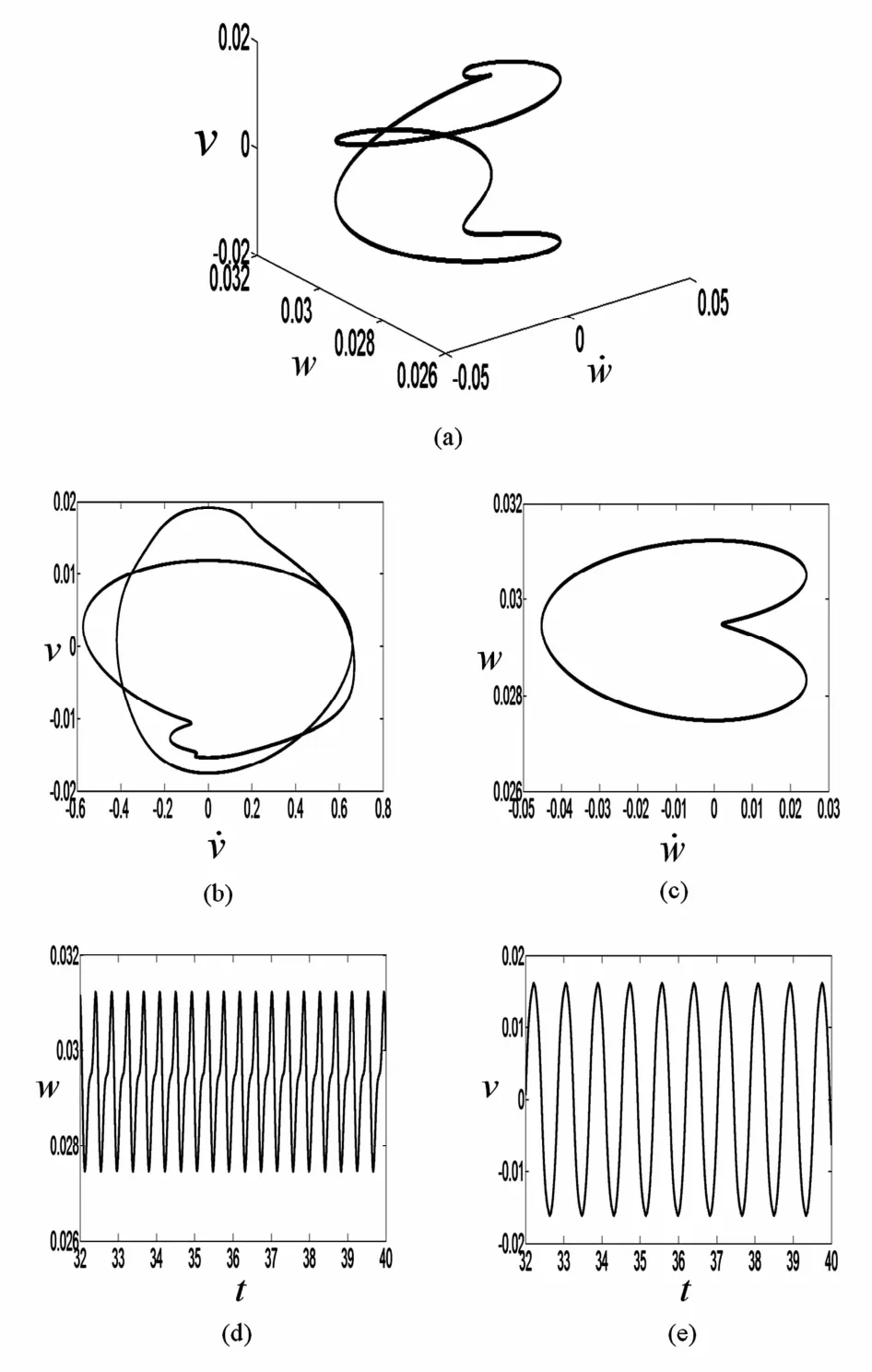
图3 c0＝20.5m／s，c1＝0.5525m／s时周期运动Fig.3 Periodic motion appears when c0＝20.5m／s，c1＝0.5525m／s

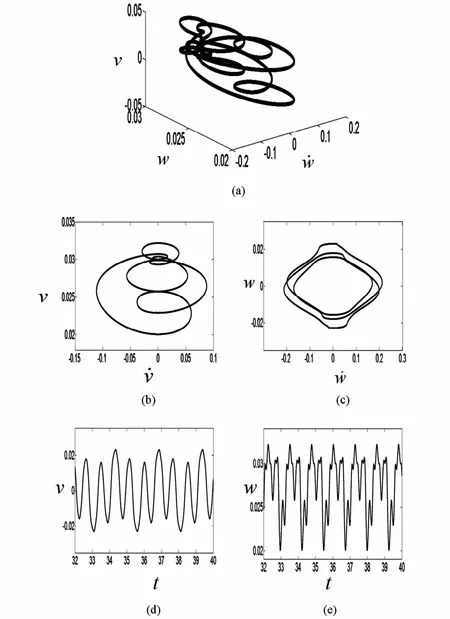
图4 c0＝20.5m／s，c1＝1.3325m／s时周期运动Fig.4 Periodic motion appears when c0＝20.5m／s，c1＝1.3325m／s

图5 c0＝16m／s，c1＝2.1m／s时混沌运动Fig.5 Chaotic motion appears when c0＝16m／s，c1＝2.1m／s

4 结论

用微分求积法对轴向移动粘弹性梁面内和面外振动耦合的非平面非线性振动的动力学行为进行了分析.利用分叉图分别研究了轴向运动定常速度和轴向运动速度变化幅值对轴向移动梁非平面振动的影响.为了具体地描绘由分叉图得到的轴向移动梁非平面振动的非线性动力学性质，作出了一些典型的周期运动和混沌运动的相图和时间历程图.以上研究结果表明微分求积法能够有效地用来分析轴向移动梁高维非线性系统的动力学性质.

1 Özkaya E，PakdemirliM.Vibrations of an axially accelerating beam with small flexural stiffness.Journal of Sound and Vibration，2000，234（3）：521～535

2 Marynowski K，Kapitaniak T.Kelvin-Voigt versus Burgers internal damping in modeling of axially moving viscoelastic web.International Journal of Non-linear Mechanics，2002，37：1147～1161

3 Yang X D，Chen L Q.Bifurcation and chaos of an axially accelerating viscoelastic beam.Chaos，Solitons and Fractals，2005，23：249～258

4 ChenL Q，Yang X D.Transverse nonlinear dynamics of axially accelerating viscoelastic beams based on 4-term Galerkin truncation.Chaos，Solitons and Fractals，2006，27（3）：748～757

5 Ding H，Chen L Q.On two transverse nonlinearmodels of axially moving beams.Science in China Series E：Technological Sciences，2009，52（3）：743～751

6 ChenL H，Zhang W，Yang F H.Nonlinear dynamics of higher-dimensional system for an axially accelerating viscoelastic beam with in-plane and out-of-plane vibrations.Journal of Sound and Vibration，2010，329：5321～5345

7 Ghayesh M H，Amabili M.Three-dimensional nonlinear planar dynamics of an axially moving Timoshenko beam.Archive and Applied Mechanics，2013，83：591～604

8 Shu C.Differential quadrature and its application in engineering.Berlin：Springer，2000