求解广义纳什均衡问题的指数型惩罚函数方法

许吉祥, 侯 剑, 谭彦华, 冯恩民

(1.大连理工大学 数学科学学院，辽宁 大连 116024; 2.天津职业技术师范大学 理学院，天津 300222; 3.内蒙古工业大学 管理学院，内蒙古 呼和浩特 010051; 4.河北工业大学 理学院，天津 300130)



求解广义纳什均衡问题的指数型惩罚函数方法

许吉祥1,2, 侯 剑1,3, 谭彦华4, 冯恩民1

(1.大连理工大学 数学科学学院，辽宁 大连 116024; 2.天津职业技术师范大学 理学院，天津 300222; 3.内蒙古工业大学 管理学院，内蒙古 呼和浩特 010051; 4.河北工业大学 理学院，天津 300130)

本文利用指数型惩罚函数部分地惩罚耦合约束,从而将广义纳什均衡问题(GNEP)的求解转化为求解一系列光滑的惩罚纳什均衡问题 (NEP)。我们证明了若光滑的惩罚NEP序列的解序列的聚点处EMFCQ成立,则此聚点是 GNEP的一个解。进一步,我们把惩罚 NEP的KKT条件转化为一个非光滑方程系统,然后应用带有 Armijo 线搜索的半光滑牛顿法来求解此系统。最后,数值结果表明我们的指数型惩罚函数方法是有效的。

运筹学;指数型惩罚函数;半光滑牛顿法;广义纳什均衡

0 引言

广义纳什均衡问题(generalized Nash equilibrium problem简记为GNEP)是标准的纳什均衡问题(NEP)的推广, 它允许每个参与人的目标函数和策略集都可以依赖于竞争者的策略. 这使得GNEP较NEP更适合于描述实际的竞争市场. GNEP的研究起源于1952年的经典文献[1]。1965年文献[2]考虑了所有参与人的决策都满足共享凸约束的GNEP。 随后,1991年文献[3]将GNEP变型为一个拟变分不等式(QVI),但是关于QVI的有效算法仍很少. 近期以来GNEP越来越多地被应用于建模经济、工程、交通运输、电力、计算机、通信和环境等领域中的问题(见综述文章[4]),可是对GNEP数值方法的研究却远不如对经典NEP研究的那样完善。

求解GNEP的数值方法,因问题的不同背景及目标的不同而各有差异。主要包括基于QVI变型[3]、基于正则化Nikaido-Isoda函数的优化问题变型、松弛方法、参数化变分不等式(VI)方法 (见综述文章[4,5])。但是这些方法主要是处理标准的NEP或者共享凸约束的GNEP。尽管如此,对于无特殊结构的GNEP而言,惩罚方法和使用KKT条件的方法大概是最有效的两类方法[6]。特别地,文献[7]提出了一个序列惩罚方法,其中序列中的每个惩罚问题都是SC2光滑的惩罚 NEP。文献[8]给出了一个求解GNEP的障碍函数惩罚方法。

本文的主要工作是,利用指数型惩罚函数提出一种新的求解一般形式的GNEP的序列惩罚方法,其中序列中的每个惩罚问题都是光滑的C2惩罚NEP。我们证明了若光滑的惩罚NEP序列的解序列的聚点处EMFCQ成立,则此聚点是GNEP的一个解。进一步,我们把惩罚NEP的KKT 条件转化为一个非光滑方程系统,然后再用带有Armijo线搜索的半光滑牛顿法来求解此系统。最后,数值结果表明我们的指数型惩罚函数方法是有效的。

1 GNEP的定义及预备知识

GNEP是标准的NEP的推广。具体地说,设有N个参与人,将每个参与人v∈{1,…,N}的决策变量记为xv∈nv,且令x=(x1,…,xN)T∈N是由这N个决策变量构成的向量,其中n:=n1+…+nN。为了强调第v个参与人的决策变量,有时我们也将x写成x=(xv,x-v)T,这里x-v=(x1,…,xv-1,xv+1,…xN)T∈n-v表示x中除了第v个决策变量之外的其余所有决策变量按照原来顺序构成的向量,其中n-v=n-nv。设参与人v的效用函数为θv:n→R,策略集Xv(x-v)⊆nv依赖于其余参与人的决策变量。第v个参与人的目的就是,在给定其余参与人的决策变量x-v∈n-v之后,选择自己的决策变量xv∈nv,使它满足如下极小化问题:

s.txv∈Xv(x-v)

下面介绍本文需要的两个概念：Clarke广义次微分、向量值函数的半光滑性。

令X,Y是有限维向量空间,O是X中的一个开集,Φ:O⊆X→Y是一个定义在O上的局部 Lipschitz 连续函数,由Rademacher 定理我们知道,Φ在集合O上几乎处处Fréchet可微。用DΦ表示Φ在O上所有Fréchet可微点构成的集合,则函数Φ在x∈O处的Bouligand次微分 (B-次微分) ∂BΦ(x)定义为

∂BΦ(x):={limk→∞JΦ(xk)|xk∈DΦ,xk→x}

其中JΦ(xk)为Φ在xk处的 Jacobian。

Φ在x处的Clarke意义下广义次微分定义为∂BΦ(x)的凸包[9,定理2.5.1],即∂Φ(x)=conv{∂BΦ(x)}，下面要介绍的半光滑性的概念最初由Mifflin[10]提出,之后由Qi和Sun[11]推广到了向量值函数。

定义1 令Φ:O⊆X→Y是开集O上的局部Lipschitz连续函数,则称Φ在x∈O处半光滑,若

(i)Φ在x处方向可微;

(ii)对任意XΔx→0和V∈∂Φ(x+Δx)有Φ(x+Δx)-Φ(x)-V(Δx)=o(‖Δx‖)。

进一步,我们称Φ在x∈O处强半光滑,若Φ在x处半光滑,并且对于任意XΔx→0和V∈∂Φ(x+Δx),有Φ(x+Δx)-Φ(x)-V(Δx)=O(‖Δx‖2)。

在求解一个由半光滑方程构成的系统时,下面给出的强BD-正则性条件在算法中所起的作用类似于求解一个由光滑方程构成的系统时用到的Jacobian矩阵非奇异性条件。

定义2 设Φ:n→n在x处是局部Lipschitz 连续,我们称Φ在处是强BD-正则的,若对任意的H∈∂BΦ(x),都满足H是非奇异的。进一步,若满足系统Φ(x)=0且Φ在处是强BD-正则的,那么我们称是该系统的强BD-正则解。

2 GNEP的指数型惩罚函数方法

在本文中,我们假设第v个参与人的策略集Xv(x-v)的表达形式如下:

Xv(x-v):={xv∈nv|gv(xv,x-v)≤0,hv(xv)≤0}

(1)

其中,gv:n→mv是依赖于其他参与人的决策变量的,因此它被称为GNEP的耦合约束.hv:nv→lv只依赖于第v个参与人的决策变量xv,因此它被称为GNEP的自身约束。

那么,GNEP的第v个参与人面临的优化问题如下:

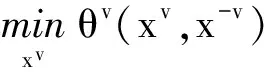
(2)

对于每个参与人v=1,…,N, 我们做以下假设:

注:上述关于GNEP的凸性的假设在GNEP的文献中是标准的假设, 而关于目标函数和约束函数的光滑性的假设是为了设计局部超线性收敛算法的需要 (见综述文章[4])。

由假设1可以知道,每一个参与人v面临的优化问题(2)都是一个凸规划,因此x*,v∈Xv(x*,-v)是(2)式的解当且仅当

〈▽xvθv(x*,v,x*,-v),xv-x*,v〉≥0, ∀xv∈Xv(x*,-v)

这里〈c,d〉代表向量c和d的内积cTd,接着通过定义

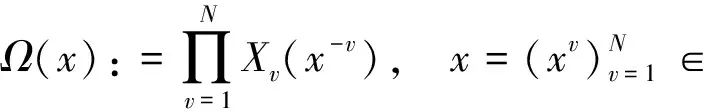
(3)

我们得到x*是GNEP的解当且仅当x*∈Ω(x*)且

〈F(x*),x-x*〉≥0, ∀x∈Ω(x*)

(4)

这是一个拟变分不等式, 我们记为 QVI(F,Ω)。

为了强调GNEP的自身约束hv的作用,我们定义集合Xv⊆nv和X⊆n如下:

Xv:={xv∈nv|hv(xv)≤

那么,第v个参与人面临的优化问题(2)也可以写为

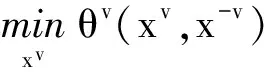
(5)

众所周知,求解一个经典NEP要比求解一个GNEP容易得多,因此 我们求解GNEP的指数型惩罚函数方法的想法就是通过部分地惩罚GNEP中的那些困难的耦合约束,使得求解GNEP等价于求解一列经典NEP。

这样得到的NEP中的第v个参与人面临的优化问题为:

(6)

接下来我们要证明,通过求解一列经典NEP(6)可以得到原GNEP(2)的解。

(7)

和映射H:n→l为

(8)

则

Ω(x)=X1(x-1)×…×XN(x-N)

可以等价地表示为如下形式

Ω(x)={y∈n|G(x,y)≤0,H(y)≤0}

相应地,我们也用QVI(F,G,H)来代表问题(4)。为了讨论方便,我们令

于是,对应于每个参与人v=1,…,N面临的优化问题(6)可以写为

(9)

并称(9)为原GNEP(2)的惩罚NEP。很显然由假设1知,任意给定x-v∈n-v,对应于每个参与人的子问题(9)都是凸的、C2光滑的优化问题,并且x∈X是惩罚 NEP的解当且仅当对于每个v=1,…,N,

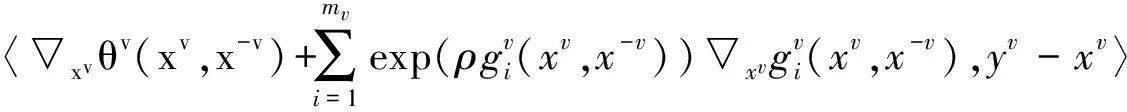
(10)

显然,组装上述所有v=1,…,N的系统可得到如下的等价系统

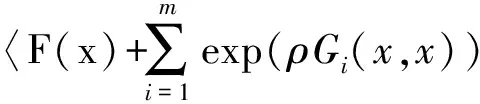
(11)

下面我们给出广义Mangasarian-Fromovitz约束规范(EMFCQ)[7]的定义, 这个定义在证明GNEP的指数型惩罚函数方法的收敛性时会用到。

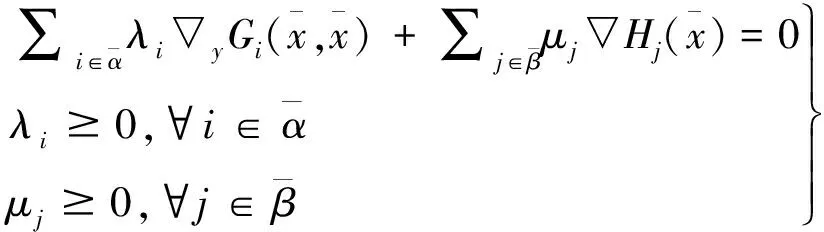
(12)

我们还需要以下引理[12,定理6.14]。

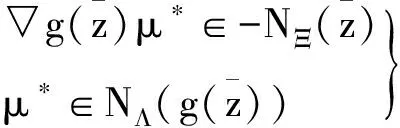
(13)

对于每个参与人v=1,…,N,我们可以将问题(5)的KKT条件写为

(14)

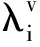
(15)

其中,λ=(λ,…,λm)T=((λ1))T,…,(λN)T)T和μ=(μ1,…,μl)T=((μ1)T,…,(μN)T)T。

下面一个引理证明了在恰当的条件下,(15)可以用来求解QVI(F,G,H)。

(16)

再由引理1可知,

因此,我们可以将(16)式等价地表示为

下面给出我们的指数型惩罚函数方法的收敛性定理。

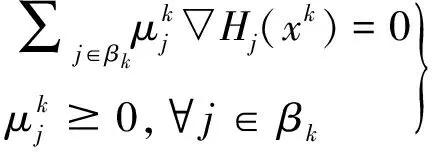
(17)

(18)

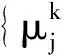
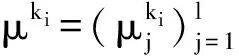
(19)

(20)

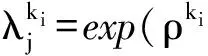
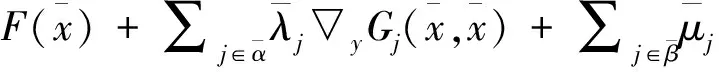
3 半光滑牛顿法求解惩罚NEP及数值结果

接着,我们应用半光滑牛顿法来求解惩罚NEP(9)。首先我们将与惩罚问题(9)等价的问题(11)的KKT系统等价地写成一个非光滑方程组的形式,然后应用带有Armijo线搜索的半光滑牛顿法来求解此系统。最后,我们给出了半光滑牛顿法求解该问题的收敛性和收敛速度，数值结果表明我们的指数型惩罚函数方法是有效的。

问题(11)的KKT条件为

(21)

(22)

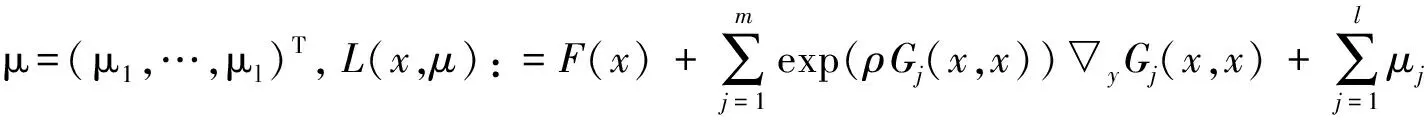
算法1

步骤1 如果‖Ψ(ωk)‖≤ε,则停止,否则转入步2。

步骤2 选取Hk∈∂Φ(ωk)。求解系统

Hkd=-Φ(ωk)

(23)

的解dk。如果(23)不可解或者求解得到的dk不满足条件

▽Ψ(ωk)Tdk≤-ρ‖dk‖k

则置dk=-▽Ψ(ωk)。

步骤3 令tk是{βj|j=0,1,2,…}中的最大者,并且满足Ψ(ωk+tkdk)≤Ψ(ωk)+tkσ▽Ψ(ωk)Tdk。

步骤4 置ωk+1=ωk+tkdk,k=k+1,转步 1。

下述定理给出了半光滑牛顿法1的收敛性和收敛速度,由于惩罚问题(9)都是凸的、C2光滑的优化问题, 故这个定理的证明可直接参考文献[13,定理11]。

定理2 假设算法1不在有限步终止,令{ωk}是由算法1产生的序列,则序列{ωk} 的每一个聚点ω*都是Ψ的稳定点。进一步,若ω*是系统Φ(ω)=0的强BD-正则解,则{ωk}超线性收敛于ω*。

注：关于ω*是Φ(ω)=0强BD-正则解的充分条件的讨论可以参考[14]。

最后,我们应用MATLAB 6.5编制了半光滑牛顿法的相应计算机程序,并求解了文献中的三个典型算例。

例1[15,16]这个算例是一个互联网网络模型。设有N个参与人,每个参与人的效用函数为

表1 例1的数值结果

例2[16]设有 3 个参与人,他们所控制的决策变量分别为x1∈3,x2∈2和x3∈2。每个参与人v的效用函数为

表2 例2的数值结果

例3[16.17]这是一个电力市场模型,在这个模型中有3个参与人。第一个参与人的决策变量x1∈,第二个参与人的决策变量)∈2,第三个参与人的决策变量)∈3。设,这三个参与人的效用函数为

和

其中Ψ(x):=2(x1+…+x6)-378.4,常数ci,di,ei的取值在表3中给出。

表3 常数ci,di,ei的取值

对于x的各个分量有如下约束条件,0≤x1≤80,0≤x2≤80,0≤x3≤50,0≤x4≤55,0≤x5≤30,0≤x6≤40。

表4列出相应的数值结果。

表4 例3的数值结果

4 结论

本文的主要工作是,利用指数型惩罚函数提出一种新的求解一般形式的GNEP的序列惩罚方法,其中序列中的每个惩罚问题都是C2光滑的惩罚NEP。我们证明了若光滑的惩罚NEP序列的解序列的聚点处EMFCQ成立,则此聚点是GNEP的一个解。特别的,因每个惩罚问题都是光滑的,从而允许我们设计局部快速的收敛算法。最后,数值结果表明我们的求解GNEP的指数型惩罚函数方法是有效的,从而进一步丰富了求解GNEP的惩罚类型方法。与文献[16]相比较知,本文的惩罚参数不必太大(ρ=100),从而求解惩罚问题时降低了遇到数值病态的可能性,而相比之下文献[16]的惩罚参数需要取到ρ=105;另一方面由于这些方法都是局部算法,对于例2而言,两个算法收敛到了两个不同的广义纳什均衡点,从而设计新的全局算法是我们进一步的研究方向。

[1] Debreu G. A social equilibrium existence theorem[J]. Proceedings of the National Academy of Sciences, 1952, 38: 886- 893.

[2] Rosen J B. Existence and uniqueness of equilibrium points for concave n-person games[J]. Econometrica, 1965, 33: 520-534.

[3] Harker P T. Generalized nash games and quasi-variational inequalities[J]. European Journal of Operational Research, 1991, 54: 81-94.

[4] Facchinei F, Kanzow C. Generalized nash equilibrium problems[J]. Annals of Operations Research, 2010, 175: 177-211.

[5] Krawczyk J. Numerical solutions to coupled-constraint(or generalised Nash)equilibrium problems[J]. Computational Management Science, 2007, 4: 183-204.

[6] Cominetti R, Facchinei F, Lasserre J B. Modern optimization modelling techniques[M]. New York: Birkhäuser, 2012. 151-188.

[7] Fukushima M, Pang J S. Quasi-variational inequalities, generalized nash equilibria, and multi-leader-follower games[J]. Computational Management Science, 2005, 2: 21-56.

[8] Hou J, Lai J F. A penalty approach for generalized nash equilibrium problem[J]. Communications In Mathematical Research, 2012, 28: 181-192.

[9] Clarke F H. Optimization and nonsmooth analysis[M]. New York: John Wiley, 1983.

[10] Mifflin R. Semismooth and semiconvex functions in constrained optimization[J]. SIAM Journal on Control and Optimization, 1977, 15: 959-972.

[11] Qi L, Sun J. A nonsmooth version of newton’s method[J]. Mathematical Programming, Ser.A, 1993, 58: 353-368.

[12] Rockafellar R T, Wets R J B. Variational analysis[M]. Springer, 1998.

[13] Luca T D, Facchinei F, Kanzow C. A semismooth equation approach to the solution of nonlinear complementarity problems[J]. Mathematical Programming, 1996, 75: 407- 439.

[14] Hou J, Zhang L W. A barrier function method for generalized Nash equilibrium problems[J]. Journal of Industrial and Management Optimization, 2014, 10: 1091-1108.

[15] Kesselman A, Leonardi S, Bonifaci V. Game-theoretic analysis of internet switching with selfish users[A]. Deng X T, Ye Y Y. Lecture Notes in Computer Science[C]. Springer, 2005, 3828: 236-245.

[16] Facchinei F, Kanzow C. Penalty methods for the solution of generalized nash equilibrium problems[J]. SIAM Journal on Optimization, 2010, 20: 2228-2253.

[17] Contreras J, Klusch M, Krawczyk J B. Numerical solutions to nash-cournot equilibria in coupled constraint electricity markets[J]. IEEE Transactions on Power Systems, 2004, 19: 195-206.

Exponential Penalty Function Method for Generalized Nash Equilibrium Problem

XU Ji-xiang1,2, HOU Jian1,3, TAN Yan-hua4, FENG En-min1

(1.SchoolofMathematicalSciences,DalianUniversityofTechnology,Dalian116024,China; 2.SchoolofSciences,TianjinUniversityofTechnologyandEducation,Tianjin300222,China; 3.ManagementCollege,InnerMongoliaUniversityofTechnology,Hohhot010051,China; 4.SchoolofSciences,HebeiUniversityofTechnology,Tianjin300130,China)

This paper reformulates the generalized Nash equilibrium problem(GNEP)as a sequence of smoothing penalized NEPs by means of a partial penalization of the coupling constraints where the exponential penalty functions are used. We demonstrate that the limit point is a solution to the GNEP under the EMFCQ at a limit point of solutions to smoothing penalized NEPs. Further more, we formulate the Karush-Kuhn-Tucker(KKT)conditions for smoothing penalized NEPs into a system of nonsmooth equations, and then apply the semismooth Newton method with Armijo line search to solve the system. Finally, the numerical results show that our exponential penalty function method for GNEP is effective.

operational research; the exponential penalty function; semismooth Newton method; generalized Nash equilibrium problem

2013- 01- 08

863项目(2007AA02Z208);973项目(2007CB714304);国家自然科学基金项目(10871033,11171050)

许吉祥(1982-)，男，博士，助教。

O225

A

1007-3221(2015)01- 0081- 08