有关非负张量的一些性质

杨瑞娟，王 翔

(天津大学理学院数学系天津300072)

在文献[1]和文献[2]中，Lim和Qi最先介绍并研究了张量的特征值.在最近几年，非负张量的最大特征值问题备受关注.Chang等在文献[3]中将P－F定理从非负矩阵推广到了非负不可约张量上，并且将非负不可约矩阵的Collatz最小最大值定理也推广到了非负不可约张量上.在文献PF定理的进一步结果[4]中，Yang等进一步的证明了非负张量Perron－Frobenius定理，并且给出了张量的谱半径的定义，更进一步在文献[5]中将文献[3]和文献[4]的一些结论从非负不可约张量推广到了非负弱不可约张量，随之求张量谱半径的算法也相继被提出.近来具有各种特殊特征的张量被广泛研究，如正张量、素张量、弱素张量、非负不可约张量、弱不可约、随机张良、本质正张量、弱正张量、严格非负张量等，对这些张量的研究主要集中在谱半径的代数、几何单性[6－7]，各种张量之间的关系，计算谱半径的算法.

1 预备知识

定义 张量是一个多维数组，一个实的m阶n维张量A是由nm个元构成:ai1…im∈R其中j=1，…，m，ij=1，…，n.一个m阶n维张量称为非负的(正的)，如果 ai1…im≥0(ai1…im＞0).

定义 若存在(λ，x)∈C×Cn是齐次方程Axm－1=λx[m－1]的解，则称 λ 为 A 的特征值，x 为 A的和 λ 对应的特征向量，这里 Axm－1和 x[m－1]是 n维向量.它的第i个元素是

这个定义在Qi[1]中有介绍，其中假设A是m阶n维对称张量，且m是偶数，在Lim[2]中限制x是实向量，λ是实数.

定义 张量 A的谱半径 ρ(A)=max{|λ|:λ是A的特征值}.

张量A的弱不可约和弱素定义如下:

定义 设A是m阶n维的非负张量.

2)若G(A)是可约矩阵，则称张量是A弱可约的，若A不是弱可约的，则称A是弱不可约的.类似若G(A)是素矩阵，则称A是弱素的.

定义 设A是m阶n维的非负不可约张量，令 TAx=(Ax[1/m－1])，若对任意非零非负向量 x，若存在非负整数r，使得TrA(x)＞0，则A是素张量.

称张量A是随机的.

定理 设A是m阶n维的非负张量，则有存在λ0≥0和非负向量x0≠0使得

定理 设A是m阶n维的非负弱不可约张量，ρ(A)为张量A的谱半径.那么

1)ρ(A)＞0.

2)存在惟一的正特征向量x和谱半径ρ(A)对应.

定理 设A是m阶n维的非负弱不可约张量，设(λ，y)为 A 的特征对，且|λ|ρ(A)，则|y|是惟一的与ρ(A)对应的正特征向量.

2 主要结论

定理1 若m阶n维非负张量是A随机的，令w=mini(ai…i)，则有|λ －w|≤1－w，λ 为 A 的任一特征值.

证明:设λ是m阶n维随机张量A的任一特征值，x=(x1，x2，…，xn)为 A的与 λ 对应的特征向量.令0 ＜ |xk|=maxi(|xi|)，又 λxm－1=Axm－1.所以

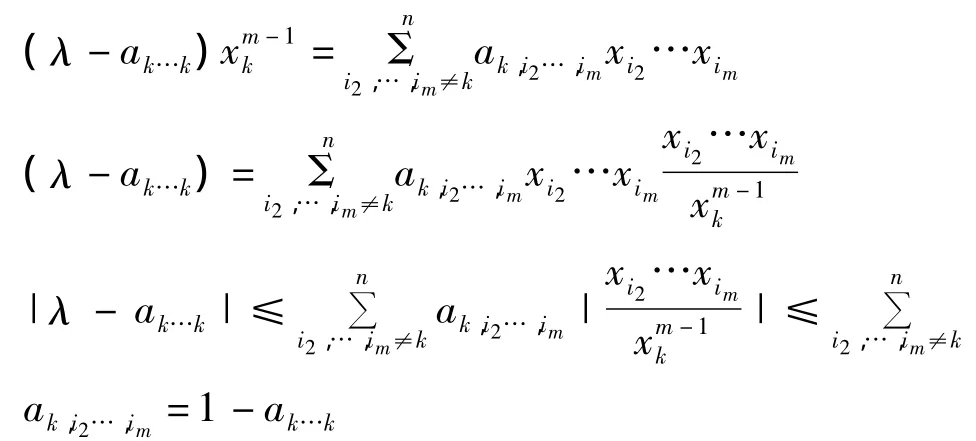
即|λ － ak…k|≤1 － ak…k.

所以|(λ －w)|=|(λ － ak…k－ w)|≤ |λ － ak…k|+ |ak…k－w|≤1 －ak…k+ak…k－w=1 －w .得证.

定理2 设A是m阶n维非负弱不可约张量，若diag(A)＞0那么A是弱素的.

证明:由于非负张量A是弱不可约的，则G(A)是不可约，又

G(A)ii= Σi∈{i2，…，im}aii2…im≥aii2…1＞0，

则由文献的定理，得G(A)是素矩阵，再由定义知是A弱素的.

定理3 设A是m阶n维的非负张量，并且m≥3，若 ai，1…1＞ 0，i=1，…，n 且，ai，j，1…1＞ 0，j=2，…，n，i是任意的，则有谱半径ρ(A)是复几何单的.

证明:由 G(A)ij= Σj∈{i2…im}ai，i2…im≥ai，j，1…1＞0，∀i=1，…，j=2，n，则G(A)ij＞0，∀i=1，…，n，j=2，…，n

当 j=1 时，ai，1，…1＞ G(A)i1= Σj∈{i2…im}ai，i2…im≥ai，j，1…1＞0.∀i=1，…，n，所以G(A)ij＞0，∀i=1，…，n

则G(A)是不可约的.∴A是弱不可约的.

由定理 3，得 Aym－1= ρ(A)ym－1，A|y|m－1，所以有，要使上式成立，

则对指标{i2…im|，ai，i2…，im＞0}，∃Φi，使

令 yi=eiΦi|yi| i=1，2，…n.

∵ ai，1…1＞0，i=1，…n，则

Φ =Φi=Φj(mod 2π)，且(m －1)φ1=Φ +2s1π，

s1∈{0，…，m －1}

由题设知 aij1…1＞0，j=1，2…，n，则有

(m －2)φ1+φj=Φ(mod 2π)，j=2，…，n则有

因此 φ =φi=φj(mod 2π).即 y=eiφ|y|也就是 y=k|y|，k∈C.

因此谱半径ρ(A)是复几何单的.

注:此定理是对文献[8]定理3.2的推广，将其中的不可约条件去掉，可以证明其仍然成立.用定理可将文献中的引理和例的不可约张量的结论推广到弱不可约张量，如下定理4、5:

定理4 若A是m阶n维非负弱不可约张量且m是偶数，设y∈Rn是ρ(A)对应的特征向量，且 y1，…，yl＞0 和 yl+1，…yn＜0，1 ＜l＜ n，这里 yi是 y的第i个元素，则对某些指标，{i，i2…，im}，ai，i2…im＞ 0，有

定理5 若A是m阶n维非负弱不可约张量且 m 是奇数，m≥3，a1，1，i…i＞ 0，i=2，…n. 则有 ρ(A)是实几何单的.(注:运用定理和定理参考文献的引理和例的证明可得).

[1]QI L.Eigenvalues of a real supersymmetric tensor[J].Journal of Symbolic Computation，2005(40):1302－1324.

[2]LIM L H.Singular values and eigenvalues of tensors:A variational approach[J].Proceedings of the IEEE International workshop on computational advances of multi－tensor adaptive processing，2005，1:129－132.

[3]CHANG K C，PEARSON K，ZHANG T.Perron － Frobenius theorem for nonnegative tensors [J].Commun.Math.Sci.，2008，6:507－520.

[4]YANG Y，YANG Q.Further results for Perron－Frobenius theorem for nonnegative tensors[J].SIAM J.Matrix Anal.Appl.，2010，31:2517－2530.

[5]YANG Q，YANG Y.Further results for Perron－Frobenius theorem for nonneg － ative tensors II[J].SIAM J.Matrix Anal.Appl.，2011，32:1236 －1250.

[6]CHANG K C，PEARSON K，ZHANG T.Primitivity，the convergence of the NZQ method，and the largest eigenvalue for nonnegative tensors[J].SIAM J.Matrix Anal.Appl.，2011，32:806－819.

[7]HU S L，HUANG Z H，QI L Q.Finding the spectral radius of a nonnegative tensor[DB/OL].http://arxiv.org.sci－ hub.org/abs/1111.2138，2011 －11 －09.

[8]YANG Y N，YANG Q Z.A note on the geometric simplicity of the spectral radius of nonnegative irreducible tensors[DB/OL].http://arxiv.org/abs/1101.2479，2011 －01 －13.

[9]HENRYK M.Nonnegative matrices[M].New York:Wiley，1988.