多涡卷超混沌系统的设计与性能分析
孙克辉,艾星星,贺少波
多涡卷超混沌系统的设计与性能分析
孙克辉1, 2,艾星星1,贺少波1
(1. 中南大学物理与电子学院,湖南长沙,410083;2. 新疆大学物理科学与技术学院,新疆乌鲁木齐,830046)
为了设计性能优越的多涡卷超混沌系统,采用理论分析和数值仿真方法,通过设计一个连续的非线性函数,得到了6阶超混沌系统的单方向与网格多涡卷吸引子模型。通过吸引子相图、Lyapunov指数谱、分岔图、Poincaré截面和复杂度等,分析了多涡卷超混沌系统的动力学特性。研究结果表明:多涡卷超混沌吸引子具有丰富的动力学特性,仿真结果与理论分析结果一致,表明了多涡卷超混沌系统设计方法的有效性和设计模型的正确性。
超混沌吸引子;多涡卷吸引子;连续非线性函数;动力学特性
超混沌系统与多涡卷混沌系统是近年来混沌领域的研究热点,Rössler[1]在1979年提出了超混沌Rössler系统。Li等[2]提出了超混沌Chen系统;Chen等[3]基于Lü系统[4]提出了超混沌系统;Nikolov等[5]提出了变形超混沌Rössler系统;Gao等[6]在Chen系统基础上产生了超混沌;王兴元等[7−9]以Lorenz系统为基础提出了超混沌Lorenz系统;李亚等[10]在Chua系统的基础上提出了一个6阶超混沌蔡氏系统。与混沌相比,超混沌具有2个或2个以上的正Lyapunov指数,相轨迹在更多的方向上分离,具有更加复杂的动力学行为。与单涡卷混沌系统相比,多涡卷混沌系统在吸引子结构上具有更加复杂的动力学行为,人们先后提出了用分段线性、阶梯波和符号函数等来产生多涡卷混沌吸引子的方法[11−16]。多涡卷超混沌系统综合了多涡卷混沌系统与超混沌系统的特性,因此,在超混沌的基础上,设计非线性函数,构造出能够产生多涡卷超混沌系统具有重要意义。本文作者首先在六阶超混沌系统的基础上,设计2类连续的非线性函数,并将连续的非线性函数应用于超混沌系统,得到单方向多涡卷超混沌吸引子,并对其进行动力学性能分析,讨论了系统参数的选取方法;然后,设计网格多涡卷超混沌吸引子,同时对网格多涡卷超混沌系统性能进行分析。
1 单方向多涡卷超混沌吸引子设计与性能分析
1.1 单方向多涡卷超混沌吸引子的建模
文献[11]构建的六阶超混沌系统方程为
构造一个连续非线性函数替代原有的非线性函数,设计系统的非线性函数(1)为:
以上非线性函数(1)是由线性的1和非线性tanh(1)组合而成。因tanh(1)是连续的,连续函数相加减还是连续的,所以,函数(1)是连续的。是线性项1的斜率,是非线性项的平移因子,可以控制产生涡卷的大小,越大,吸引子范围越大。参数的选取对非线性函数有较大的影响,越大,tanh(1)在各点的斜率越大,当趋于无穷大时,tanh(1)无限逼近符号函数。
1.2 单方向多涡卷超混沌吸引子仿真
取=0.65,=5,=9,设初始值为(0.24,0.06,0,0.01,0,0),在Matlab中利用龙格库塔法进行数值仿真,得单方向多涡卷吸引子相图如图1所示。从图1可见:涡卷数目越多,呈现完整吸引子的仿真时间就越长;利用设计的非线性函数能够得到多涡卷吸引子,并且系统在1方向产生多涡卷吸引子,得到的吸引子清晰,2的变化范围一致。

(a) 两涡卷;(b) 三涡卷;(c) 四涡卷;(d) 五涡卷;(e) 六涡卷;(f) 七涡卷
1.3 单方向多涡卷超混沌吸引子的性能分析
以四涡卷吸引子为例,分析当系统参数变化时系统的动力学特性。仿真时,参数步长均为0.002,初始值与1.2节的相同。
1) 设=5,=9,参数在[0, 1]内变化,得到四涡卷吸引子随参数变化的分岔图如图2所示。从图2可见:分岔图纵坐标分为4个区域,这与四涡卷吸引子相图相对应。计算四涡卷吸引子关于参数的Lyapunov指数谱如图3所示。图3中,Lyapunov指数谱在[0.092,0.76]范围内存在2个正的Lyapunov指数,可见系统在该区间处在超混沌状态,与图2所示的分岔图显示的范围相一致。
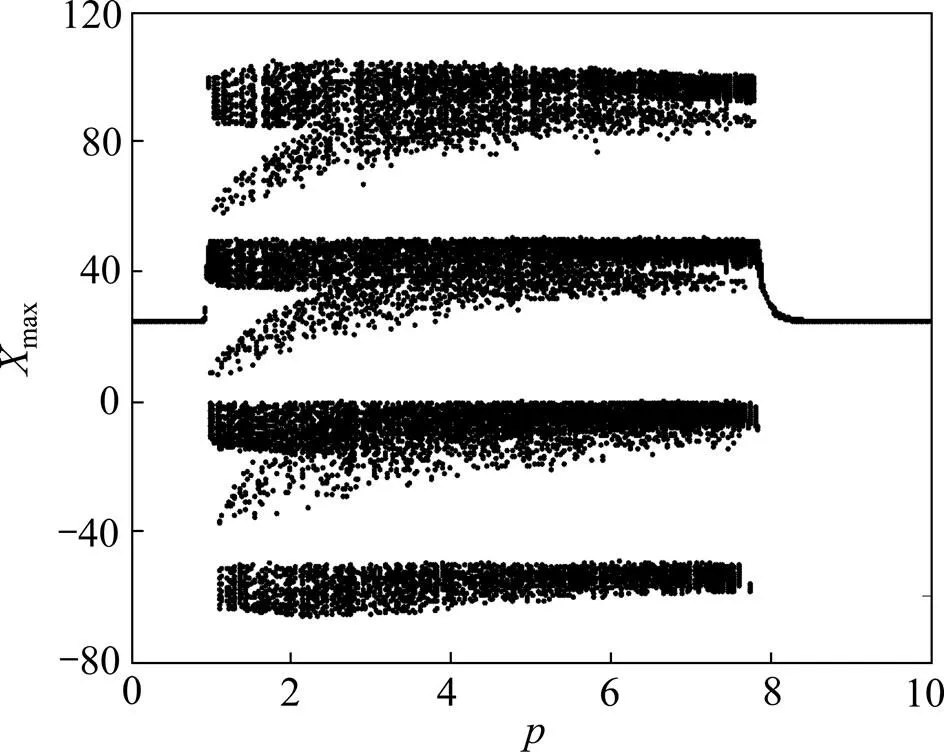
图2 四涡卷吸引子关于参数k变化的分岔图

图3 系统随参数k变化的Lyapunov指数谱
2) 设=0.65,=9,参数在[0.1, 10]范围内变化,得四涡卷吸引子的关于参数的分岔图如图4(a)所示。从图4(a)可见:随着参数增大,分岔图呈现持续增长趋势,说明吸引子大小随参数增加而变大,通过改变能够控制涡卷。为了考察系统的分岔特性,将区间[0.14, 0.20]放大,并据对称初值可得分岔图如图4(b)所示,可见系统存在叉式分岔。分别取0.150,0.155,0.167,0.170和0.200,=0.65,=9,以1对对称的(±0.24,±0.06,0,±0.01,0,0)数值为初始值,得到1对对称的相图如图5所示。图5中(a),(c),(e),(j),(i)是以(−0.24,−0.06,0,−0.01,0,0)为初始值,图5中(b),(d),(f),(h),(j)是以(0.24,0.06,0,0.01,0,0)为初始值。从图5可见:系统随着参数的变化,系统的分岔形式有叉式分岔和倍周期分岔,系统经历周期状态、单涡卷吸引子、两涡卷吸引子和四涡卷吸引子,呈现十分丰富的动力学行为。同样,计算四涡卷吸引子关于参数的Lyapunov指数谱如图6所示,其中有2个Lyapunov指数相近,所以在图上靠得很近。由图6可见:Lyapunov指数谱在[0.514,10.000]范围内存在2个正的Lyapunov指数,可见系统在该区间处在超混沌状态,而且在[0.156, 0.514]区间中,也存在不连续的超混沌区间。

(a) p在区间[0,10]的分岔图;(b) 区间放大图

(a) 以(−0.24,−0.06,0,−0.01,0,0)为初值,p=0.150,1周期;(b) 以(0.24,0.06,0,0.01,0,0)为初值,p=0.150,1周期;(c) 以(−0.24,−0.06,0,−0.01,0,0)为初值,p=0.155,2周期;(d) 以(0.24,0.06,0,0.01,0,0)为初值,p=0.155,2周期;(e)以(−0.24,−0.06,0,−0.01,0,0)为初值,p=0.167,单涡卷;(f) 以(0.24,0.06,0,0.01,0,0)为初值,p=0.167,单涡卷;(g) 以(−0.24,−0.06,0,−0.01,0,0)为初值,p=0.170,两涡卷;(h)以(0.24,0.06,0,0.01,0,0)为初值,p=0.170,两涡卷;(i) 以(−0.24,−0.06,0,−0.01,0,0)为初值,p=0.200,四涡卷;(j) 以(0.24,0.06,0,0.01,0,0)为初值,p=0.200,四涡卷

图6 系统随参数p变化的Lyapunov指数谱
3) 设=0.65,=5,参数在[0.1, 12]范围内变化,四涡卷吸引子的关于参数的分岔图如图7所示。将区间[0.24, 0.4]放大可得图8,并且分别取0.26,0.28,0.30,0.32,=0.65,=5,以1对对称的(±0.24,±0.06,0,±0.01,0,0)为初始值,通过数值仿真得到1对对称的相图如图9所示。图9中(a),(c),(e)和(g)是以(−0.24,−0.06,0,−0.01,0,0)为初始值,图9中(b),(d),(f)和(h)是以(0.24,0.06,0,0.01,0,0)为初始值。从图9可见:系统随着参数的变化呈现叉式分岔和倍周期分岔,系统具有极限环、单涡卷、混沌和超混沌等十分丰富的动力学行为。计算四涡卷吸引子关于参数的Lyapunov指数谱如图10所示。从图10可见:Lyapunov指数谱在[0.286,12.000]范围内存在2个正的Lyapunov指数,可见系统在该区间处在超混沌状态,与图7结果一致。

图7 四涡卷吸引子关于参数n变化的分岔图

图8 n区间放大后的分岔图

(a) 以(−0.24,−0.06,0,−0.01,0,0)为初值,n=0.26,1周期;(b) 以(0.24,0.06,0,0.01,0,0)为初值,n=0.26,1周期;(c) 以(−0.24,−0.06,0,−0.01,0,0)为初值,n=0.28,2周期;(d) 以(0.24,0.06,0,0.01,0,0)为初值,n=0.28,2周期;(e) 以(−0.24,−0.06,0,−0.01,0,0)为初值,n=0.30,单涡卷;(f)以(0.24,0.06,0,0.01,0,0)为初值,n=0.30,单涡卷;(g) 以(−0.24,−0.06,0,−0.01,0,0)为初值,n=0.32,四涡卷;(h)以(0.24,0.06,0,0.01,0,0)为初值,n=0.32,四涡卷

图10 系统随参数n的Lyapunov指数谱
4) 设=0.65,=5,=9,分别计算二、三、四、五、六、七涡卷共6个Lyapunov指数,结果见表1。从表1可见:每个系统都有2个正的Lyapunov指数,表明系统处于多涡卷超混沌状态。

表1 单方向多涡卷超混沌系统的Lyapunov指数
5) 为了更好地验证系统的混沌特性,计算2=0.1为截面的四涡卷超混沌吸引子的Poincaré截面,如图11所示。从图11可知:截面上的点主要密集地分布在4条并行的线上,说明系统处于四涡卷超混沌吸引子状态;截面上,2条并行线之间的点是键带上的点,说明涡卷之间通过键带连接在一起。

图11 四涡卷超混沌吸引子的Poincare截面图
6)混沌序列复杂度是指其接近随机性的程度,越接近随机序列,复杂度越大[18],将其用于保密通信被破译的难度越大。文献[18]提出了一种基于强度统计算法的混沌序列复杂度的分析。算法具有灵敏度高且对参数嵌入维和序列长度的选择要求不严格等特点,计算的复杂度值越小,序列越复杂。本文利用该算法对多涡卷超混沌系统的复杂性进行分析,选取嵌入维=5,取1的20 000个数据作为输入混沌序列,利用上述算法计算单方向多涡卷超混沌系统的复杂度,如表2所示。从表2可见:在单方向多涡卷超混沌系统中,随着涡卷数目的改变,复杂度几乎没有变化,处于同一个数量级。所以,就复杂度而言,若将多涡卷超混沌系统应用于保密通信,则选取任意涡卷数目都是可行的,但多涡卷在吸引子相图上表现出来涡卷数目越多,各维变量的取值范围越大,得到混沌序列所需要的时间越长,故在选取应用对象时需要综合复杂度、取值范围以及实时性等综合考虑。而且从表2可以看出复杂度不理想,与离散系统的复杂度相比大1个数量级。文献[17]提出通过伪随机序列扰动来增加混沌伪随机序列的复杂度,这使得通过该方法得到的复杂度已经不是混沌伪随机序列的复杂度。本文提供一个简便的方法,只要将得到的序列每隔一定的区间取样,再计算其复杂度,这样得到的复杂度只取决于混沌序列,而与其他序列的复杂度无关。例如每间隔100个点再取样,所得结果见表2。从表2可见:在每隔100个点再取样之后,复杂度有了明显提高,而且数量级与文献中计算出离散混沌系统的复杂度相当。通过合适的数据处理,可提高连续混沌系统混沌序列的复杂度,为该混沌序列的应用提供了理论依据。

表2 单方向多涡卷超混沌系统的复杂度
2 网格多涡卷超混沌吸引子的设计与性能分析
2.1 网格多涡卷吸引子的建模
网格多涡卷超混沌吸引子在不同的方向上同时产生多涡卷,具有更复杂的拓扑结构。为了设计网格多涡卷超混沌吸引子,在2方向上引入1个非线性项,其微分方程为
其中:(1)控制1方向的涡卷数目;(2)为控制2方向涡卷的数目。
式中,为线性项的斜率;为非线性项的平移因子,能够控制产生涡卷的大小,越大,吸引子范围越大;为比例因子,控制2方向平衡点的位置。
2.2 网格多涡卷超混沌吸引子仿真
设=0.5,=0.5,=0.5,=10 000,初始值选取与1.2节中的相同,在Matlab中利用龙格库塔法进行数值仿真,得网格多涡卷超混沌吸引子相图如图12所示。从图12可见:通过在1和2方向同时引入连续的非线性函数能够在2个方向同时产生多涡卷,得到的吸引子清晰,大小一致,而且可通过改变非线性函数得到任意数目的多涡卷超混沌吸引子。
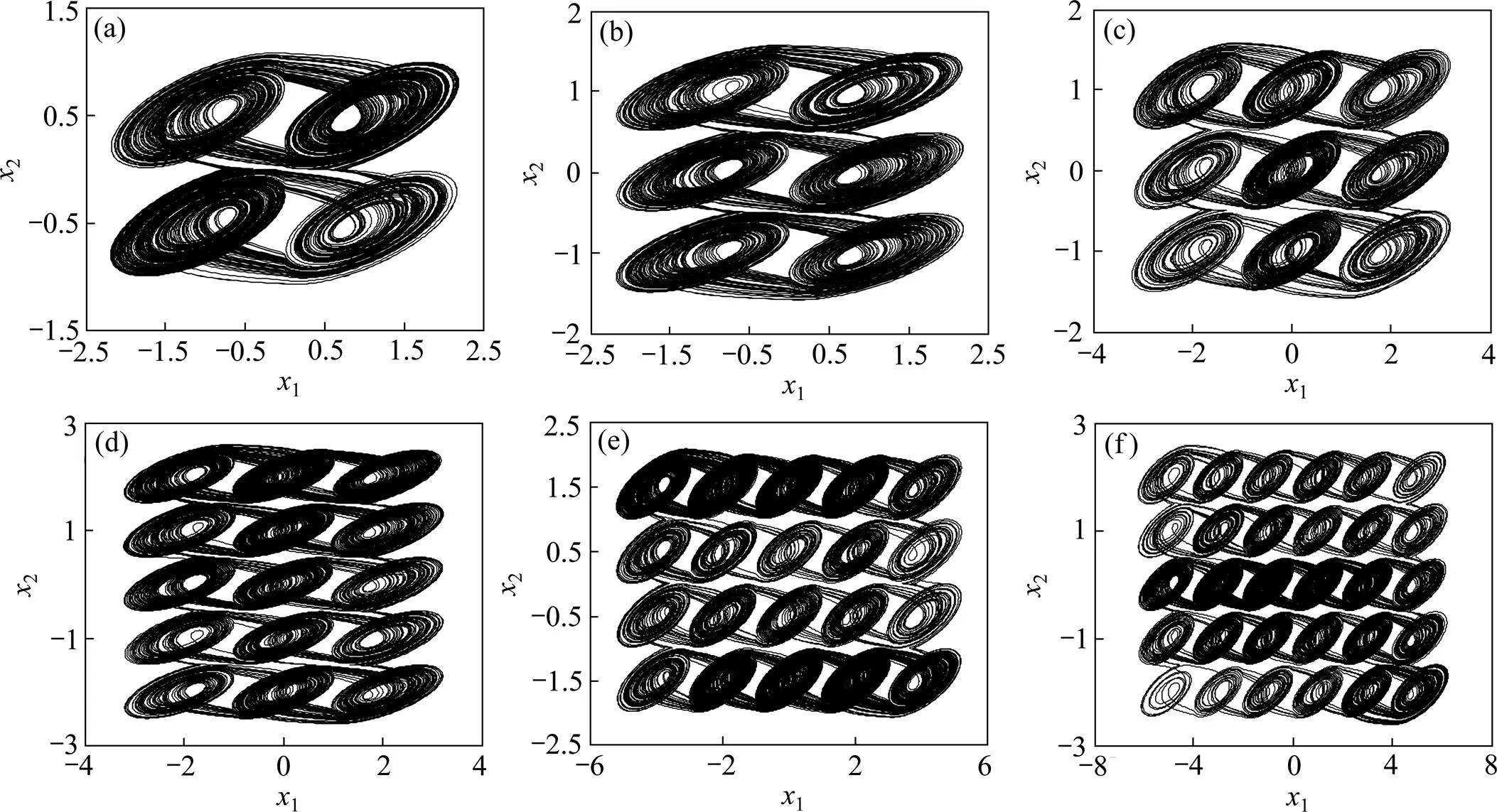
(a) 2×2多涡卷;(b) 2×3多涡卷;(c) 3×3多涡卷;(d) 3×5多涡卷;(e) 5×4多涡卷;(f) 6×5多涡卷
2.3 网格多涡卷超混沌吸引子的性能分析
以2×2网格多涡卷超吸引子为例,分析系统参数变化时系统的动力学特性,仿真步长均为0.002。
1) 设=0.5,=0.5,=10 000,参数在[0.15, 1.50]内变化,计算2×2网格多涡卷吸引子关于参数的最大Lyapunov指数曲线如图13(a)所示。从图13(a)可见:在[0.556, 1.180]内存在2个正的Lyapunov指数,系统在该区间内处于超混沌状态。
2)设=0.5,=0.5,=10 000,参数变化,且Î[0, 1.8],得到2×2网格多涡卷吸引子关于参数的Lyapunov指数谱如图13(b)所示。从图13(b)可见:在区间[0.264, 1.800]存在2个正的Lyapunov指数,表明系统处于超混沌状态。
3)=0.5,=0.5,=10 000,参数变化,且Î[0, 1.2],得到2×2网格多涡卷吸引子关于参数的Lyapunov指数谱如图13(c)所示。从图13(c)可见:[0, 0.06]和[0.39, 1.002]存在2个正的Lyapunov指数,表明系统是超混沌的。
4)设=0.5,=0.5,=0.5,参数在[9 999, 10 001]内变化,得到2×2网格多涡卷吸引子关于参数的最大Lyapunov指数曲线如图13(d)所示。从图13(d)可见:在[9 999, 10 001]范围内有2个正的Lyapunov指数,表明在该范围内系统是超混沌的。

参数:(a) k; (b) p; (c) q; (d) n
5) 为了更好地验证系统的超混沌特性,计算2=−0.5为截面的2×2网格多涡卷吸引子Poincaré截面图,如图14所示。从图14可知:截面上的点主要密集地分布在4条并行的线上,说明系统是处于2×2网格多涡卷超混沌吸引子的状态;并行线外的点是键带上的点,表明涡卷通过键带连接在一起。

图14 2×2多涡卷系统的Poincaré截面
6) 设=0.5,=0.5,=0.5,=10 000,得到计算2×2,2×3,3×3,3×5,5×4和6×5网格多涡卷超混沌吸引子的Lyapunov指数如表3所示。从表3可见:每个系统都有2个正的Lyapunov指数,表明系统处于多涡卷超混沌状态。

表3 网格多涡卷超混沌系统的Lyapunov指数
7) 同样地,选取嵌入维=5,取1的20 000个数据作为输入混沌序列,利用文献[18]中的复杂度计算方法计算网格多涡卷的复杂度,序列为每隔100个点再取样值,其复杂度计算结果如表4所示。从表4可见该方法也能够提高序列的复杂度。

表4 网格多涡卷超混沌系统的复杂度
3 结论
1) 研究了多涡卷超混沌系统的建模、仿真与动力学特性问题,在已有的六阶超混沌系统的基础上,通过设计连续的非线性函数得到了单方向与网格的多涡卷超混沌吸引子,得到的吸引子相图清晰,涡卷幅度相同。
2) 多涡卷超混沌系统具有丰富的动力学特性,多涡卷超混沌系统的理论分析结果与数值分析得到的结果相一致,说明设计方法可行。多涡卷超混沌系统的复杂度随涡卷数目的变化不大,但通过间隔取样可以增大序列的复杂度,为混沌序列的应用提供了依据。多涡卷超混沌吸引子的电路实现及其应用有待下一步研究。
[1] Rössler O E. An equation for hyperchaos[J]. Physics Letters A, 1979, 71(2): 155−157.
[2] LI Yuxia, Tang W K S, CHEN Guangrong. Generating hyperchaos via state feedback control[J]. International Journal of Bifurcation and Chaos, 2011, 15(10): 3367−3375.
[3] CHEN Aimin, LU Junan, LÜ Jinhu, et al. Generating hyperchaotic Lü attractor via state feedback control[J]. Physica A, 2006, 364: 103−110.
[4] LÜ Jinhu, CHEN Guangrong. A new chaotic attractor coined[J]. International Journal of Bifurcation and Chaos, 2002, 12(3): 659−661.
[5] Nikolov S, Clodong S. Occurrence of regular, chaotic and hyperchaotic behavior in a family of modified Rössler hyperchaotic systems[J]. Chaos Solitons & Fractals, 2004, 22(2): 407−431.
[6] GAO Tiegang, CHEN Zengqiang, YUAN Zhuzhi, et al. A hyperchaos generated from Chen system[J]. International Journal of Modern Physics C, 2011, 17(4): 471−478.
[7] 王兴元, 王明军.超混沌Lorenz系统[J]. 物理学报, 2007, 56(9): 5136−5141. WANG Xingyuan, WANG Mingjun. Hyperchaotic Lorenz system[J]. Acta Physica Sinica, 2007, 56(9): 5136−5141.
[8] Nikolov S, Clodong S. Occurrence of regular, chaotic and hyperchaotic behavior in a family of modified Rössler hyperchaotic systems[J]. Chaos Solitions Fractals, 2004, 22(2): 407−431.
[9] 高秉建, 陆军安, 陈爱敏. 一个unified系统与Rössler系统的组合研究[J]. 物理学报, 2006, 55(9): 4450−4454. GAO Bingjian, LU Junan, CHEN Aimin. A novel chaotic system via combining a unified system with Rössler system[J]. Acta Physica Sinica, 2006, 55(9): 4450−4454
[10] 李亚, 张正明, 陶志杰. 一个超混沌六阶蔡氏电路及其硬件实现[J]. 物理学报, 2009, 58(10): 6818−6822. LI Ya, ZHANG Zhengming, TAO Zhijie. A hypherchaotic sixth-order Chua’s circuit and its hardware implementation[J]. Acta Physica Sinica, 2009, 58(10): 6818−6822.
[11] Turk M, Ogras H. Recognition of multi-scroll chaotic attractors using wavelet-based neural network and performance comparison of wavelet families[J]. Expert Systems with Applications, 2010, 37: 8667−8672.
[12] YU Simin, LÜ Jinhu, CHEN Guanrong. A family of n-scroll hyperchaotic attractors and their realization[J]. Physics Letters A, 2007, 364: 244−251.
[13] Sanchez-Lopez C. Automatic synthesis of chaotic attractors[J]. Applied Mathematics and Computation, 2011, 217(9): 4350−4358.
[14] Xu F, Yu P. Chaos control and chaos synchronization for multi-scroll chaotic attractors generated using hyperbolic functions[J]. Journal of Mathematical Analysis and Applications, 2010, 362: 252−274.
[15] LI Guanlin, CHEN Xiyou. Constructing piecewise linear chaotic system based on the heteroclinic Shil’nikov theorem[J]. Communications in Nonlinear Science and Numerical Simulation, 2009, 14: 194−203.
[16] LIU Chunxia, YI Jie, XI Xiangchun, et al. Research on the multi-scroll chaos generation based on Jerk mode[J]. Procedia Engineering, 2012, 29: 957−961.
[17] 孙克辉, 贺少波, 盛利元. 基于强度统计算法的混沌序列复杂度分析[J]. 物理学报, 2011, 60(2): 020505. SUN Kehui, HE Shaobo, SHENG Liyuan. Complexity analysis of chaotic sequence based on the intensive statistical complexity algorithm[J]. Acta Physica Sinica, 2011, 60(2): 020505.
Design of multi-scroll hyperchaotic system and analysis on its characteristic
SUN Kehui1, 2, AI Xingxing1, HE Shaobo1
(1. School of Physics and Electronics, Central South University, Changsha 410083, China;2. School of Physics Science and Technology, Xinjiang University, Urumqi 830046, China)
To establish a multi-scroll hyperchaotic system with complex structure and good performance, based on theoretical analysis and simulation methods, single direction and grid multi-scroll models were presented by designing a continuous nonlinear function from a six-order hyperchaotic system. Dynamical characteristics of multi-scroll hyperchaotic attractor were analyzed by observing attractors phase diagram, Lyapunov exponents spectrum, bifurcation diagram, Poincaré section and complexity. The results show that the multi-scroll hyperchaotic attractors have rich dynamical characteristics. Simulation results are accordant with those of the theoretical analysis, which shows that the method of designing multi-scroll hyperchaotic system is effective and the designed model is correct.
hyperchaotic attractor; multi-scroll attractor; continuous nonlinear function; dynamic characteristic
10.11817/j.issn.1672-7207.2015.05.014
TP271
A
1672−7207(2015)05−1663−10
2014−05−12;
2014−07−15
国家自然科学基金资助项目(61161006, 61073187);中央高校基本科研业务费资助项目(72150050650) (Projects(61161006, 61073187) supported by the National Natural Science Foundation of China; Project(72150050650) supported by the Fundamental Research Funds for the Central Universities)
孙克辉,教授,博士,从事混沌理论与应用研究;E-mail: kehui@csu.edu.cn
(编辑 陈灿华)

