Robust Stability of a Class of Fractional Order Hopfield Neural Networks

Xiao-Lei Liu， Ming-Jiu Gai， Cui-Ling Ma， and Xiao-Yan Liu

Robust Stability of a Class of Fractional Order Hopfield Neural Networks

Xiao-Lei Liu， Ming-Jiu Gai， Cui-Ling Ma， and Xiao-Yan Liu

—As the theory of the fractional order differential equation becomes mature gradually， the fractional order neural networks become a new hotspot. The robust stability of a class of fractional order Hopfield neural network with the Caputo derivative is investigated in this paper. The sufficient conditions to guarantee the robust stability of the fractional order Hopfield neural networks are derived by making use of the property of the Mittag-Leffler function， comparison theorem for the fractional order system， and method of the Laplace integral transform. Furthermore， a numerical simulation example is given to illustrate the correctness and effectiveness of our results.

Index Terms—Fractional order neural networks，Mittag-Leffler function， robust stability.

1. Introduction

In 1982， J. Hopfield presented the Hopfield neural networks:

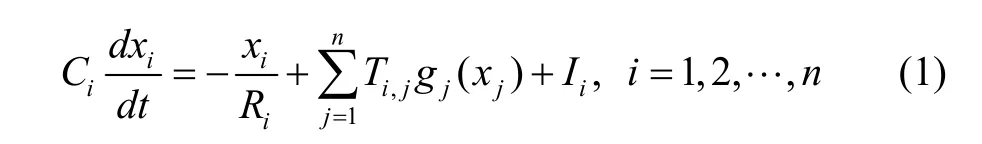
whereiR，iC， and，ijT denote the resistance， capacitance， and conductance， respectively；denotes the activation function which is yielded by the amplifier；iI denotes the external inputs. Henceforth， the Hopfield neural network has been increasingly investigated， and extended to the delayed Hopfield neural networks［1］， the Hopfield neural networks with a discontinuous activation function［2］-［3］， and so on. In recent years， the fractional order neural networks become a hotspot， as the theory of the fractional order differential equation gradually maturing［4］-［5］.

In 2009， by changing the capacitor into a kind of generalized capacitor， Arefeh Boroomand and Mohammad B. Menhaj［6］presented the fractional order Hopfield neural networks， as follows:

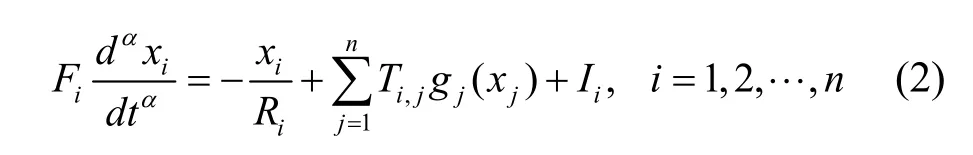
The rest of this paper is organized as follows. In Section 2， some necessary definitions and lemmas are presented. In Section 3， we study the robust stability for a class of fractional order Hopfield neural networks and give some sufficient conditions. One example and corresponding numerical simulation are used to illustrate the validity and feasibility of the results in Section 4. And conclusions are drawn in Section 5.

2. Preliminaries

There are several definitions of the fractional derivative of order α， which is the extended concept of integer order derivative. The commonly used definitions are Grunwald-Letnikov， Riemann-Liouville， and Caputo definitions. In this section， we will recall the definition of Caputo fractional derivative and the several important lemmas.

Definition 1. The Caputo fractional derivative of order α+∈ℝ of a function （）x t is defined as

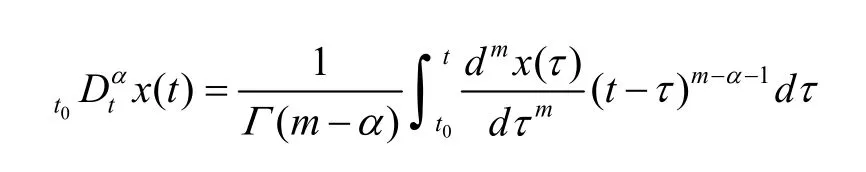
where+ℝ denotes the set of all positive real numbers，is the mth derivative ofin the usual sense and ℕ is the set of all natural numbers， andis the gamma function， i.e.，

Definition 2. The Mittag-Leffler functionand the two parameter Mittag-Leffler functionare defined as

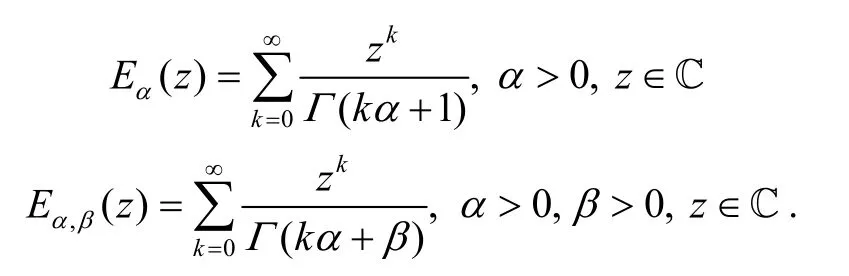
The Laplace integral transforms of the Caputo fractional derivative of orderand the Mittag-Leffler function are calculated as

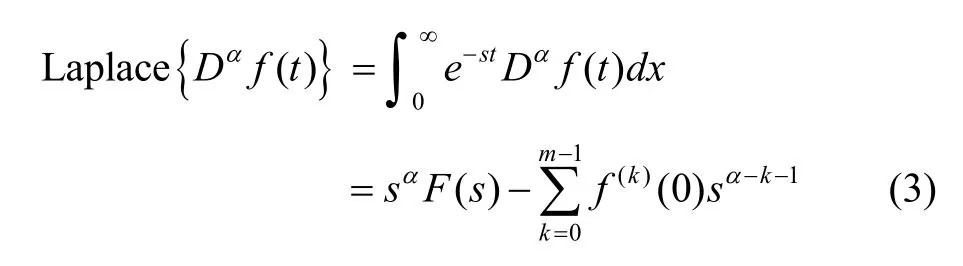
Consider the Cauchy problem of the following fractional differential equation:

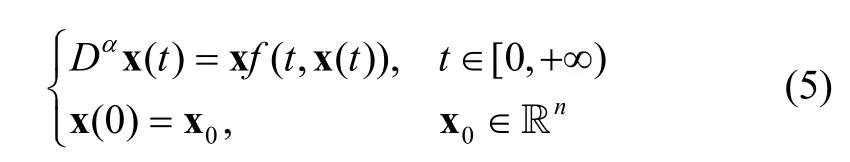
Definition 3. The constant x*is an equilibrium point of （5）， if and only iffor any.

where μ is a positive real number satisfying， and spec（）A denotes the eigenvalues of matrix A， arg（⋅） is the principal argument of a complex number， anddenotes the spectrum norm of the matrix.

Lemma 2［10］. （Gronwall-Bellman inequality） If

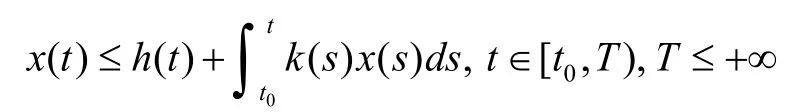
where （）x t， （）h t， and （）k t are continuous on0［，）t T，and （）0k t＞ ， then （）x t satisfies

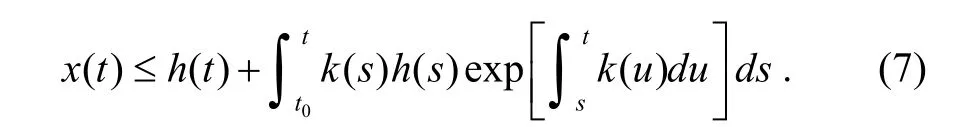
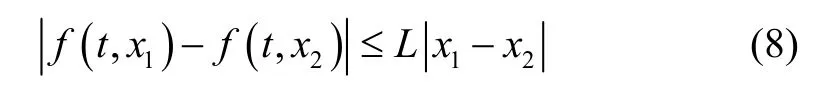
3. Robust Stability of Fractional Order Hopfield Neural Network

Consider the following fractional order Hopfield neural network:

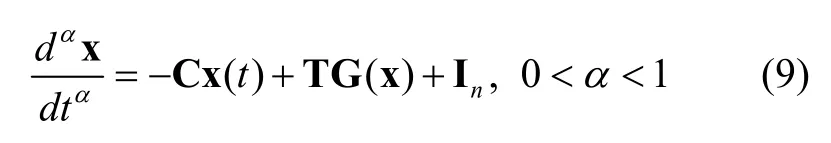
and its disturbing system

denotes the activation function of the jth neuron， wheredenotes the constant connection weight of the jth neuron on the ith neuron；represents the rate with which the ith neuron will reset its potential to the resting state when the ith neuron is disconnected from the network；，iI denotes external inputs andnℝ is the n-dimensional vector space； ΔC and ΔT denote the disturbing functions which are variable with t in the system （10）.

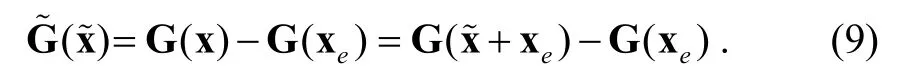
By using （11）， the system （10） is translated into

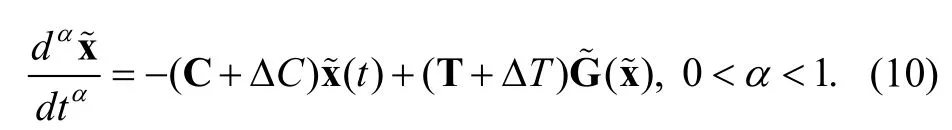
In brief， we neglect the symbol ‘～’， so the system （10）can be expressed as

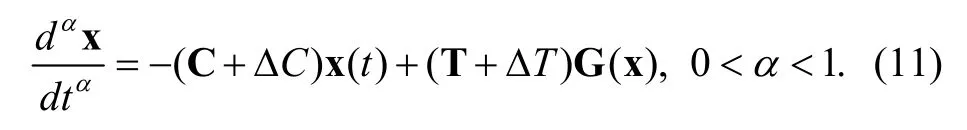
Obviously， 0=x is the equilibrium point of the system （13）. Therefore， to prove the robust stability of the equilibrium point of the system （9）， i.e.， the asymptotic stability of the equilibrium point of the system （10）， is equivalent to prove the asymptotic stability of the zero solution of the system.

Theorem 1.

（H2） If （）G x is Lipschitz-continuous in x， and， where the vector norm is the Euclidean norm which is consistent with the spectrum norm of matrices， then 0=x is a asymptotic stable equilibrium point of the system （13）.

Proof: Consider the auxiliary system as follows:

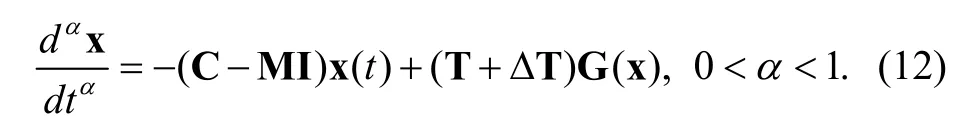
Obviously， 0=x is the equilibrium point of the system （14）. We first prove that it is an asymptotic stable equilibrium point.

Taking the Laplace transform on （14）， we have

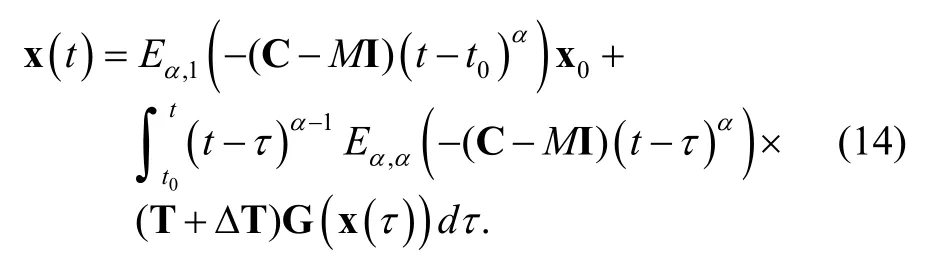
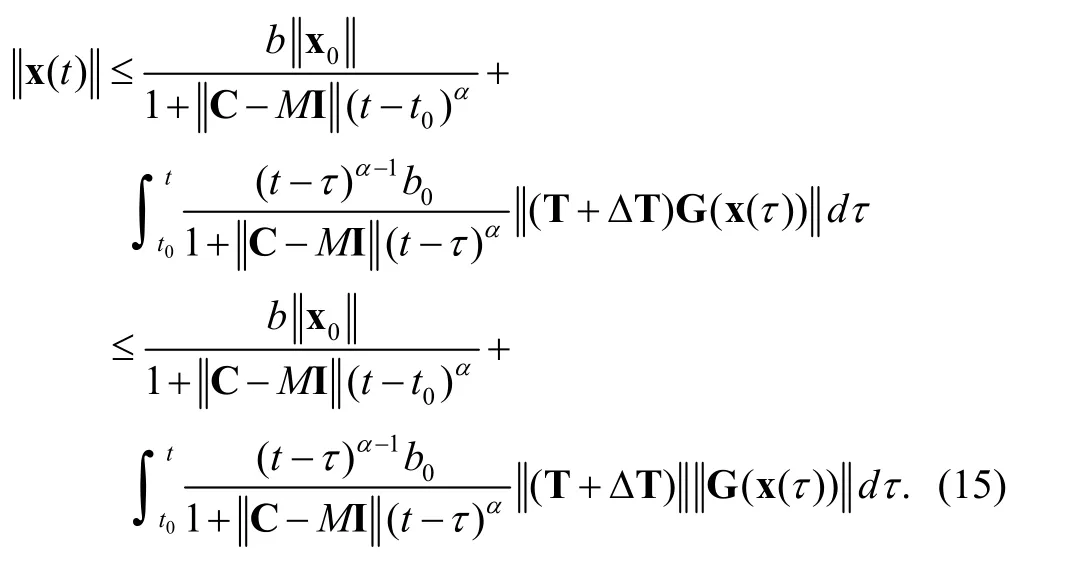
By using （17） and （18）， we get

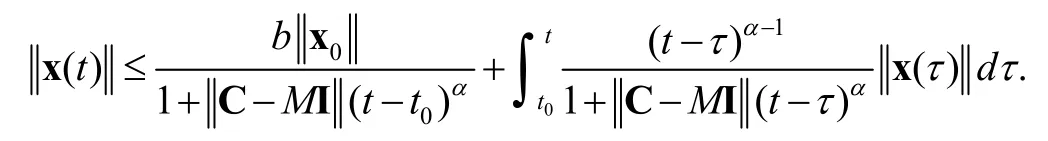
From Lemma 2， we get

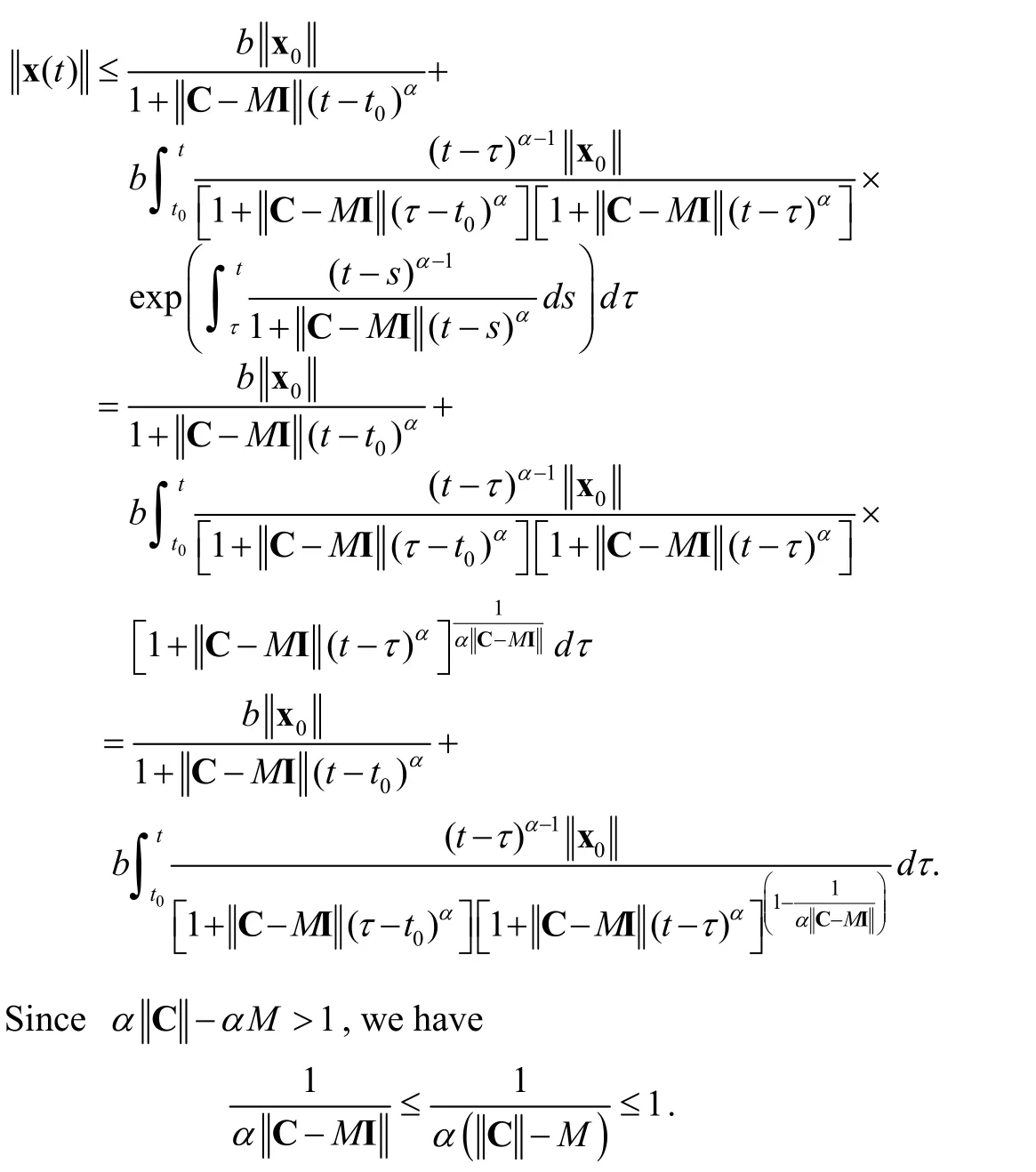
Then

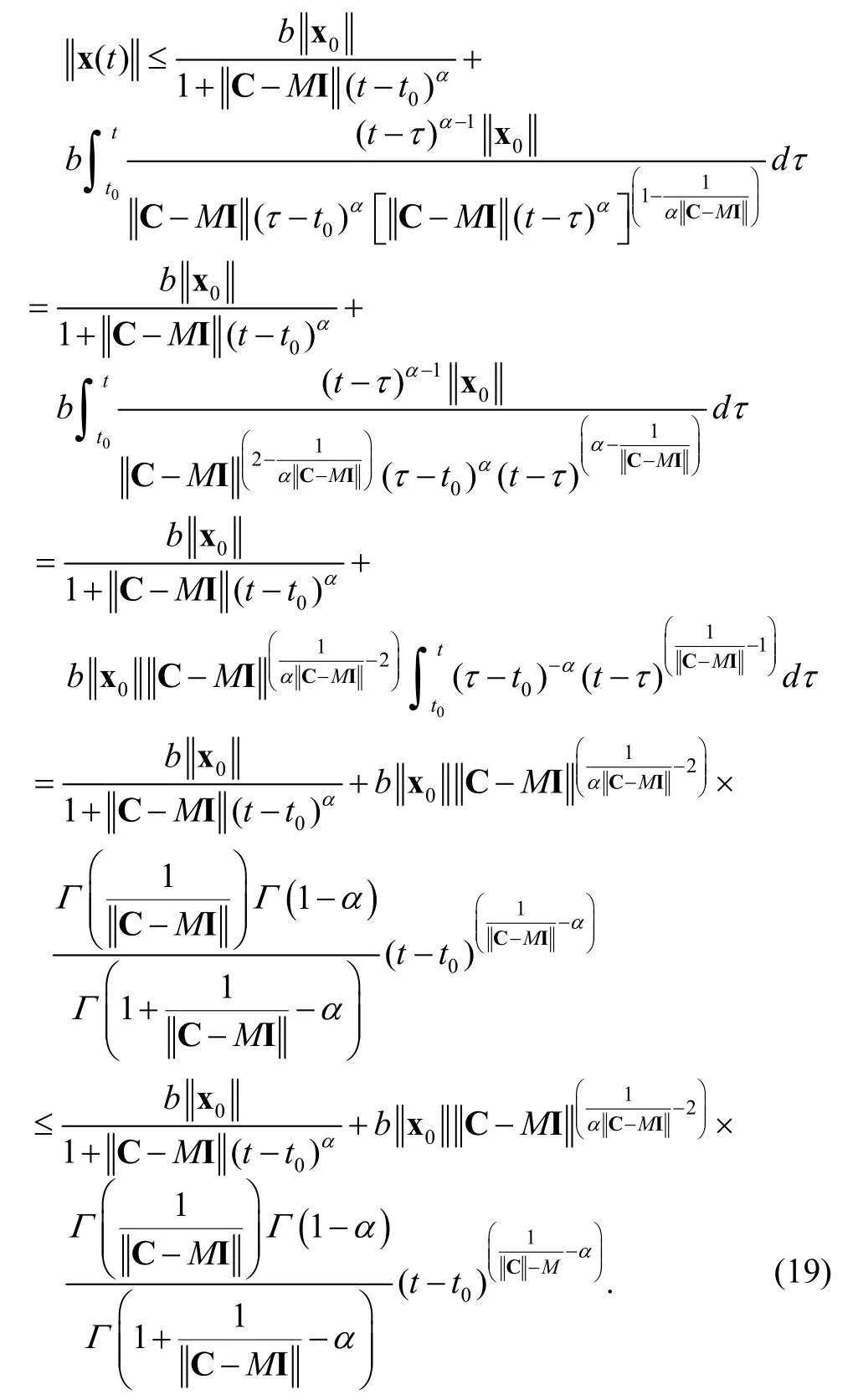
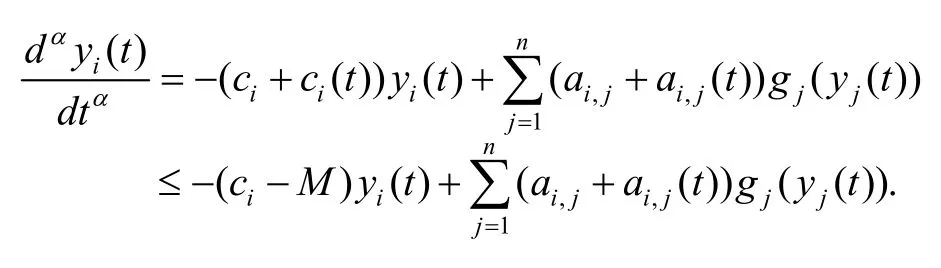
It can be written by using matrices as

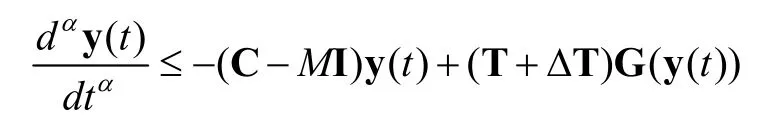
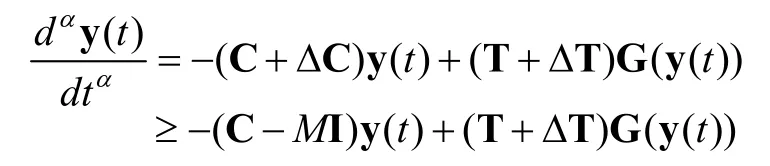
4. Illustrative Examples

In the system （13）， let

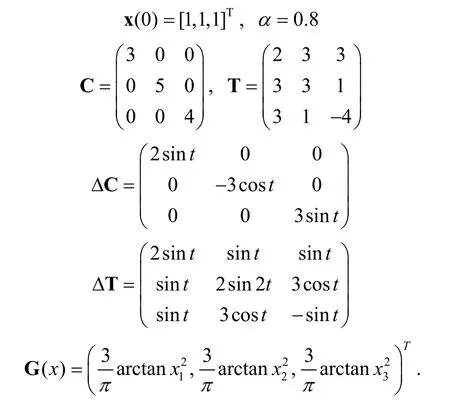
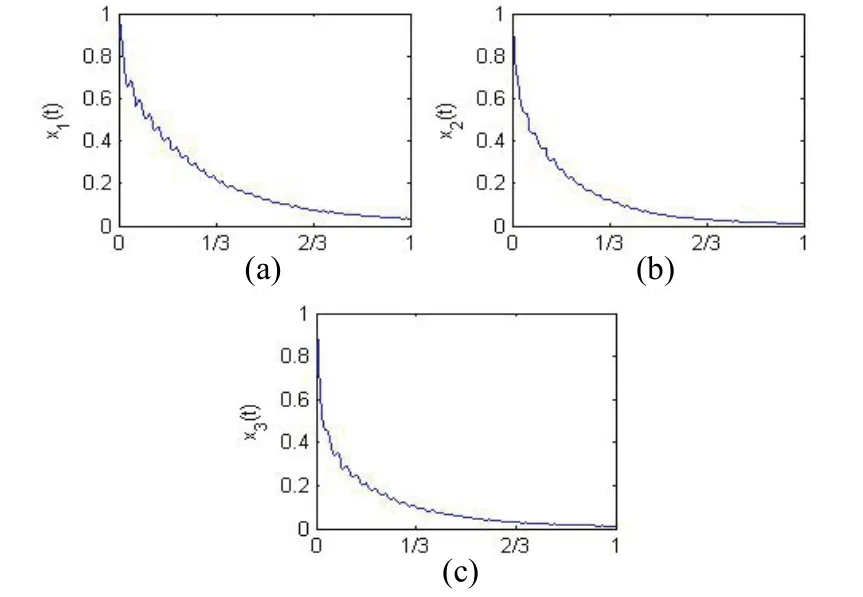
Fig. 1. Phase plot of the fractional order Hopfield neural networks:（a）plane， （b）plane， and （c）plane.

Then the system （13） satisfies the condition of Theorem 1， therefore 0=x is an asymptotic stable equilibrium point as shown in Fig. 1. From the figure，we can find that ΔC and ΔT indeed change the solution of the system （13）， but when，， and according to （H1） and （H2）， the affection of them is finite. And finally 0=x is still asymptotic stable.

5. Conclusions

In this paper， the robust stability of fractional order Hopfield neural networks was studied when 0 ＜ α＜ 1. Firstly， a fractional order auxiliary systems was constructed， and by using the method of the integral transform， it was translated into an integral equation. And then by making use of the property of the Mittag-Leffler function and Gronwall-Bellman inequality， the integral equation was investigated. Finally，the sufficient conditions of robust stability for the fractional order Hopfield neural networks were gotten by the compare theorem of fractional order systems. At last，the correctness of the conclusion was verified by the emulating example.

［1］ H.-G. Zhang， Synthetic Analysis and Research of Dynamical Specificity for the Recursive Delayed Neural Networks，Beijing: Science Publishing Company， 2008.

［2］ J.-F. Wang， L.-H. Huang， and Z.-Y. Guo， “Dynamical behavior of delayed Hopfield neural networks with discontinuous activations，” Applied Mathematical Modelling，vol. 33， no. 4， pp. 1793-1802， 2009.

［3］ L.-H. Huang， J.-F. Wang， and X.-N. Zhou， “Existence and global asymptotic stability of periodic for Hopfield neural networks with discontinuous activations，” Nonlinear Analysis: Real World Applications， vol. 10， no. 3， pp. 1651-1661， 2009.

［4］ L.-P. Chen， Y. Chai， R.-C. Wu， T.-D. Ma， and H.-Z. Zhai，“Dynamic analysis of a class of fractional-order neural networks with delay，” Neurocomputing， vol. 111， pp. 190-194， Jul. 2013.

［5］ K. Sayevand A. Golbabaib， and A. Yildirimc， “Analysis of differential equations of fractional order，” Applied Mathematical Modelling， vol. 36， no. 9， pp. 4356-4364，2012.

［6］ A. Boroomand and M. B. Menhaj， “Fractional-order Hopfield neural networks，” Lecture Notes in Computer Science， vol. 5506， no. 1， pp. 883-890， 2009.

［7］ K. Diethelm and N. J. Ford， “Analysis of fractional differential equations，” Journal of Mathematical Analysis and Applications， vol. 265， no. 2， pp. 229-248， 2002.

［8］ S.-Q. Zhang， “The existence of a positive solution for a nonlinear fractional differential equation，” Journal of Mathematical Analysis and Applications， vol. 252， no. 2， pp. 804-812， 2000.

［9］ X.-J. Wen， Z.-M. Wu， and J.-G. Lu，. “Stability analysis of a class of nonlinear fractional-order systems，” IEEE Trans. on Circuits and System II， vol. 55， no. 11， pp. 1178-1182， 2008.

［10］ C. Corduneanu， Principles of Differential and Integral Equations， Boston: AMS Chelsea Publishing， 1977.

［11］ A. A. Kilbas， H .M. Srivastava， and J. J. Trujillo， Theory and Applications of Fractional Differential Equations，Amsterdam: Elsevier， 2006.

［12］ H. Delavari， D. Baleanu， and J. Sadati， “Stability analysis of Caputo fractional-order nonlinear systems revisited，”Nonlinear Dynamics， vol. 67， no. 4， pp. 2433-2439， 2011.

Xiao-Lei Liu was born in Shandong Province， China in 1983. He received the B.S. degree in 2005 and the M.S. degree in 2008 from Qingdao University. Currently， he is working as a lecturer with Naval Aeronautical Engineering Institute. His research interests include fractional order dynamic systems and neural networks.

Ming-Jiu Gai was born in Shandong Province，China in 1964. He received his Ph.D. degree in 2001 from Naval Aeronautical Engineering Institute， Yantai， China. Now， he works as a professor with Naval Aeronautical Engineering Institute. Prof. Gai has published 3 books and over 40 journal papers. His current research interests include basic theories of nonlinear systems.

Cui-Ling Ma was born in Shandong Province， China in 1981. She received the B.S. degree in 2004 and the M.S. degree in 2007，both from the Lanzhou University. Currently，she is working as a lecturer with Naval Aeronautical Engineering Institute. Her research interests include fuzzy mathematics and complex networks.

Xiao-Yan Liu was born in Shandong Province， China in 1983. She received the B.S. and M.S. degrees from the University of Electronic Science and Technology of China in 2005 and 2008， respectively. Currently， she is working as a lecturer with Naval Aeronautical Engineering Institute. Her research interests include reliability theory and complex networks.

Manuscript received September 24， 2014； revised January 8， 2015. This work was supported by the Natural Science Foundation of Shandong Province under Grant No. ZR2014AM006.

X.-L. Liu， C.-L. Ma， and X.-Y. Liu are with the Institute of System Science and Mathematics， Naval Aeronautical and Astronautical University， Yantai 264001， China （e-mail: lxlhaitao1000@163.com；malingzwh@126.com； xiaoyanliu83@163.com）.

M.-J. Gai is with Institute of System Science and Mathematics， Naval Aeronautical and Astronautical University， Yantai 264001， China（Corresponding author e-mail: gaimingjiu@sina.com）

Digital Object Identifier: 10.3969/j.issn.1674-862X.2015.02.012