基于混合模重构的kNN回归

龚永红　宗　鸣　朱永华　程德波

1(广西师范大学广西多源信息挖掘与安全重点实验室　广西 桂林 541004)

2(桂林航天工业学院图书馆　广西 桂林 541004)

3(广西师范大学计算机科学与信息工程学院　广西 桂林 541004)

4(广西大学计算机与电子信息学院　广西 南宁 530004)



基于混合模重构的kNN回归

龚永红1,2宗鸣1,3朱永华4程德波1,3

1(广西师范大学广西多源信息挖掘与安全重点实验室广西 桂林 541004)

2(桂林航天工业学院图书馆广西 桂林 541004)

3(广西师范大学计算机科学与信息工程学院广西 桂林 541004)

4(广西大学计算机与电子信息学院广西 南宁 530004)

摘要对于线性回归中kNN(k-Nearest Neighbor)算法的k值固定问题和训练样本中的噪声问题，提出一种新的基于重构的稀疏编码方法。该方法用训练样本重构每一个测试样本，重构过程中，l1-范数被用来确保每个测试样本被不同数目的训练样本来预测，以此解决kNN算法固定k值问题；l2,1-范数导致的整行稀疏被用来去除噪声样本，以避免数据集上的噪声对重构产生不利影响。实验在UCI数据集上显示：新的改进算法比原来的kNN算法在线性回归中具有更好的预测效果。

关键词线性回归稀疏编码重构l1-范数l2,1-范数噪声样本

KNN REGRESSION BASED ON MIXED-NORM RECONSTRUCTION

Gong Yonghong1,2Zong Ming1,3Zhu Yonghua4Cheng Debo1,3

1(Guangxi Key Lab of Multi-source Information Mining and Security,Guangxi Normal University,Guilin 541004,Guangxi,China)2(Guilin University of Aerospace Technology Library,Guilin 541004,Guangxi,China)3(School of Computer Science and Information Technology,Guangxi Normal University,Guilin 541004,Guangxi,China)4(School of Computer,Electronics and Information,Guangxi University,Nanning 530004,Guangxi,China)

AbstractThis paper proposes a new reconstruction-based sparse coding method for solving the problem of k value fixing of k-NN in linear regression and the problem of noise in training samples. The method reconstructs every test sample using training sample. In reconstruction process,thel1-norm is used to ensure each test sample will be predicted by training sample in different numbers and thus to solve the problem of k-NN algorithm in fixingkvalue,and the entire row sparse incurred byl2,1-norm is used to remove noise samples so as to prevent the noise in dataset from adverse impact on the reconstruction. Experimental results on UCI datasets show that the new improved algorithm outperforms the previous k-NN regression method in terms of prediction effect.

KeywordsLinear regressionSparse codingReconstructionl1-norml2,1-normNoise sample

0引言

kNN算法是一种应用广泛的分类方法，它是最近邻算法(NN算法)的推广形式。NN算法最早是由Cover和Hart在1967年提出，最早用于分类的研究[1]。kNN算法也可用于回归：对于一个测试样本，在所有训练样本中选取最接近它的k个样本的均值来进行预测。然而本文发现传统的kNN算法对每一个测试样本，都用同样k个数目的训练样本来进行预测，这在应用中不合实际。

图1所示一个数据集分布，三角形代表测试样本，圆圈代表训练样本，如设k=3，用kNN算法预测测试样本，对于左边的测试样本，用最邻近的三个训练样本去预测，这比较合理。但对于右边的测试样本，仅有两个训练样本离它比较近，另一个离得很远，显然用最邻近的这三个训练样本来预测测试样本是不合理的，应该根据实际情况，选取不同的k值。

图1　k=3时两个测试样本

对此，一些学者展开了选取最优k值的研究。例如Cora等人提出了自动选取最优k值的kNN方法[2]。Matthieu Kowalski在稀疏扩展方法里引入了结构化稀疏的概念[3]，同时将这种方法与多层信号扩展方法联系起来，用来分解由许多不同成分构成的信号。Hechenbichler等人提出了加权kNN法[4]，该方法根据训练样本到测试样本距离的大小赋予不同的权值，距离大的权值反而小，该方法的分类识别率对k值的选取不再敏感。Zhang等人提出了代价敏感分类方法[5-8]。还有一些学者从特征加权的角度提出了一些算法，也在一定程度上改进了kNN算法。

但是以上这些方法都是只利用了训练样本中k个邻近样本提供的信息，没有考虑测试样本提供的信息，即没有考虑训练样本和测试样本之间的相关性。而本文认为样本之间是存在相关性的，对于每个测试样本，应该用与之相关的训练样本来对其进行预测，但是每一个测试样本却可能跟不同数目的训练样本相关。为此，本文用训练样本重构[9]每一测试样本获得样本之间的k相关性，同时用LASSO(the Least Absolute Shrinkage and Selection Operator)[10]来控制稀疏性以解决k值固定问题。另外实际数据集中一般会有噪声存在[11,12]，如在图1中设k=7，对于左边的测试样本，图中左上角的噪声样本会影响其真实值的预测，并应该剔除这些噪声样本，本文借助l2,1-范数能产生整行为0的特性来去除噪声。因此，针对kNN算法存在的这两个问题，本文提出一种新的基于混合模[13]重构的kNN算法—Mixed-Norm Reconstruction-kNN，简记为MNR-kNN。

1基于混合模重构的kNN算法

1.1重构

用训练样本重构每一测试样本时，本文假设有训练样本空间X∈Rn×d，n为训练样本数目，d为样本维数；测试样本空间Y∈Rd×m，m为测试样本数目。一般我们用最小二乘法[14,15]解决线性回归问题，即获取投影矩阵W∈Rn×m：

(1)

其中，‖·‖F是Frobenius矩阵范数，yi∈Rd×1，wi是W的第i列向量。

分类问题中yi一般为类标签，W表示Y与X的函数关系，在本文yi表示第i个测试样本，而W表示训练样本和测试样本经过重构得到的相关性系数矩阵。以下面例子进一步说明W，假设有4个训练样本，2个测试样本，样本属性数目为3，此时Y-XTW为:

(2)

由XTW知W中元素Wij表示第i个训练样本与第j个测试样本之间的相关性大小，Wij>0时代表正相关，Wij<0时代表负相关，Wij=0时代表不相关。所以，W表示测试样本与训练样本之间的相关性矩阵，本文考虑训练样本和测试样本之间的相关性，利用重构方法获得了训练样本与测试样本之间的相关性大小。

1.2正则化

一般得到的W不是稀疏的，考虑到列向量Wj表示第j个测试样本与所有训练样本的相关性，如果列向量中有r个元素值不为0，其余为0，则预测时k相应地取r，并用对应的这r个训练样本来预测测试样本。这样选取的k个训练样本就是与测试样本最相关的k个样本，也就可以解决kNN算法中k值固定问题。

通常使用最小二乘损失函数求解线性回归问题，即：

(3)

虽然上面目标函数是凸的，易知其解W*=(XXT)-1XY。然而，实际应用中XXT不一定可逆，为此，优化函数式(3)被加上一正则化因子，即：

(4)

(5)

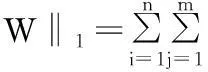
通过1.2节的方法可以求解目标函数式(5)得到的W，如下形式：

其中，W的第二行全为0，即行稀疏。这是由于l2,1-范数导致的结果，这表明第二个训练样本跟所有测试样本无关。因此，第二个训练样本可能是噪音样本。此外第一列有两个非零值，即第一个和第四个，可以说第一个测试样本与第一、第四个训练样本相关。因此对第一个测试样本预测时k=2。以此类推，如第二列有三个非零值，所以对第二个测试样本而言k=3，对第四个测试样本k=2。这就解决了kNN算法中k值固定问题，即对于不同测试样本k值是不一样的。而kNN算法中的k值通常由用户决定，本文每个测试样本的k值是通过稀疏学习得到的，是一种数据驱动分析方法。

1.3MNR-kNN算法

根据以上例子，目标函数式(5)利用l2,1-范数查找除了存在于训练集中的噪音样本，而且还利用l1-范数学习出与每个测试样本相关的训练样本。每个测试样本相关的训练样本的个数不同，即为kNN回归学习出了合适的k。这样的学习方法是数据驱动的，也解决了本文提出kNN回归存在的两个问题，即噪音样本避免问题和固定k值问题。

本文预测测试样本时用W列的非零值对应的训练样本去预测，当然此时k的取值等于W相应列非零值的个数，这种方法本文称为不加权MNR-kNN算法。但是考虑到W中的元素值大小表示测试样本和训练样本的相关性大小，相应的训练样本和测试样本之间的相关度大小是不同的，元素值越大，表明相关度越大；元素值越小，表明相关度越小。因此本文预测时根据Wj中的元素值对相应的训练样本做加权处理，可以得出第j个测试样本的加权预测值：

(6)

其中，ytrain(i)表示第i个训练样本的真实值，即第i个训练样本的类标号。这种回归方法本文称为加权MNR-kNN算法。

最后，本文给出加权/不加权MNR-kNN算法的步骤，见算法1。

算法1 加权/不加权MNR—kNN输入:样本数据输出:预测值1)将数据进行规范化处理2)通过算法2(下面给出)得到最优解W3)加权/不加权情况下MNR-kNN算法对所有测 试样本计算出相应的k值4)根据k值,通过式(6)计算测试样本的预测 值(注:不加权的情况相应的用1代替W中的 非零值即可)

2算法优化分析

虽然式(5)是凸的，但后面两项正则化都是非光滑的。为此，本文提出一种有效的算法去求解目标函数。

具体地，首先对wi(1≤i≤m)求导并命其为0，可得：

(7)

(8)

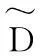
算法2:目标函数优化算法输入:X,Y输出:W(t)∈Rn×m1)初始化W1∈Rn×m,t=1;2) do{(1)计算对角矩阵D(t)i(1≤i≤m)和D~(t),其中D(t)i第k个对角元素为12|w(t)ki|,D~(t)第k个对角元素为12‖(w(t))k‖2;(2)For每个i(1≤i≤m), w(t+1)i=(XXT+ρ1D(t)i+ρ2D~(t))-1Xy(i);(3)t=t+1;}until收敛

定理1算法2在每次迭代中目标值减小。

证明根据算法里的第2步可得到：

(9)

因此有：

Tr(XTW(t+1)-Y)T(XTW(t+1)-Y)+

≤Tr(XTW(t)-Y)T(XTW(t)-Y)+

⟹Tr(XTW(t+1)-Y)T(XTW(t+1)-Y)+

≤Tr(XTW(t)-Y)T(XTW(t)-Y)+

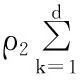
3实验结果与分析

实验数据来自UCI机器学习库[18]，具体细节见表1。

表1　数据集基本情况

本次实验主要是比较kNN算法、不加权MNR-kNN算法和加权MNR-kNN算法这三种算法的预测效果，本文选用经典评价指标RMSE和相关系数CorrCoef。RMSE和CorrCoef定义分别如下：

(10)

(11)

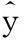
RMSE一般用来作为算法效果的评判依据，通常RMSE越小，预测值和真实值之间的偏差就越小，算法的效果也就越好，否则越差。CorrCoef表示预测值和真实值之间的相关性大小，一般相关性越大，预测越准确，反之相反。另外本文用Matlab编程实现具体程序代码，在每个数据集上用10折交叉验证法做十次实验来看算法效果。为了保证公平性，kNN算法、不加权MNR-kNN算法和加权MNR-kNN算法在每一次实验中选用相同的训练集和测试集，记录这三种算法十次实验取得的RMSE和CorrCoef情况。

图2—图5为四个数据集上的实验结果，纵坐标为RMSE的大小，横坐标为十次实验次序。

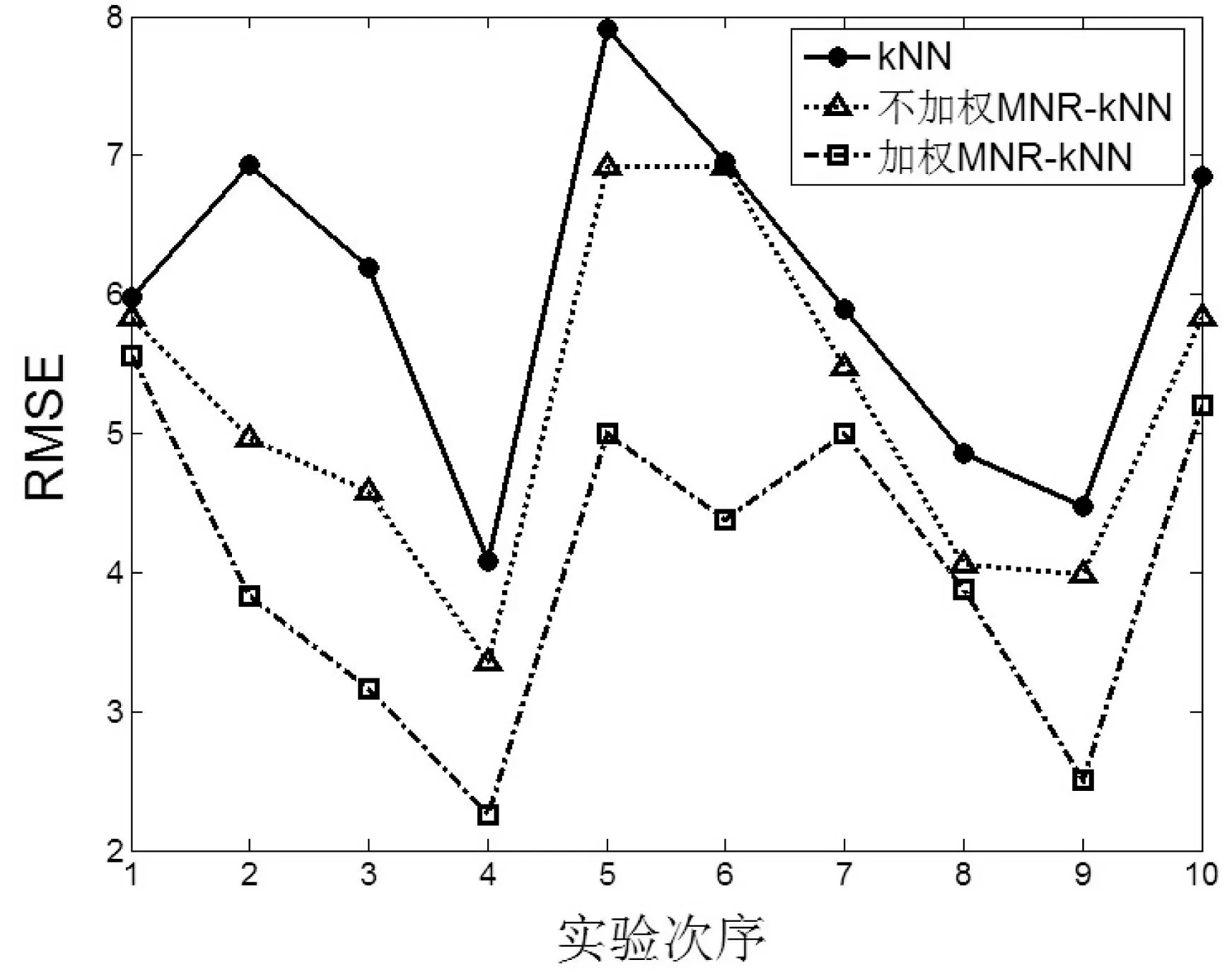
图2　数据集ConcreteSlump

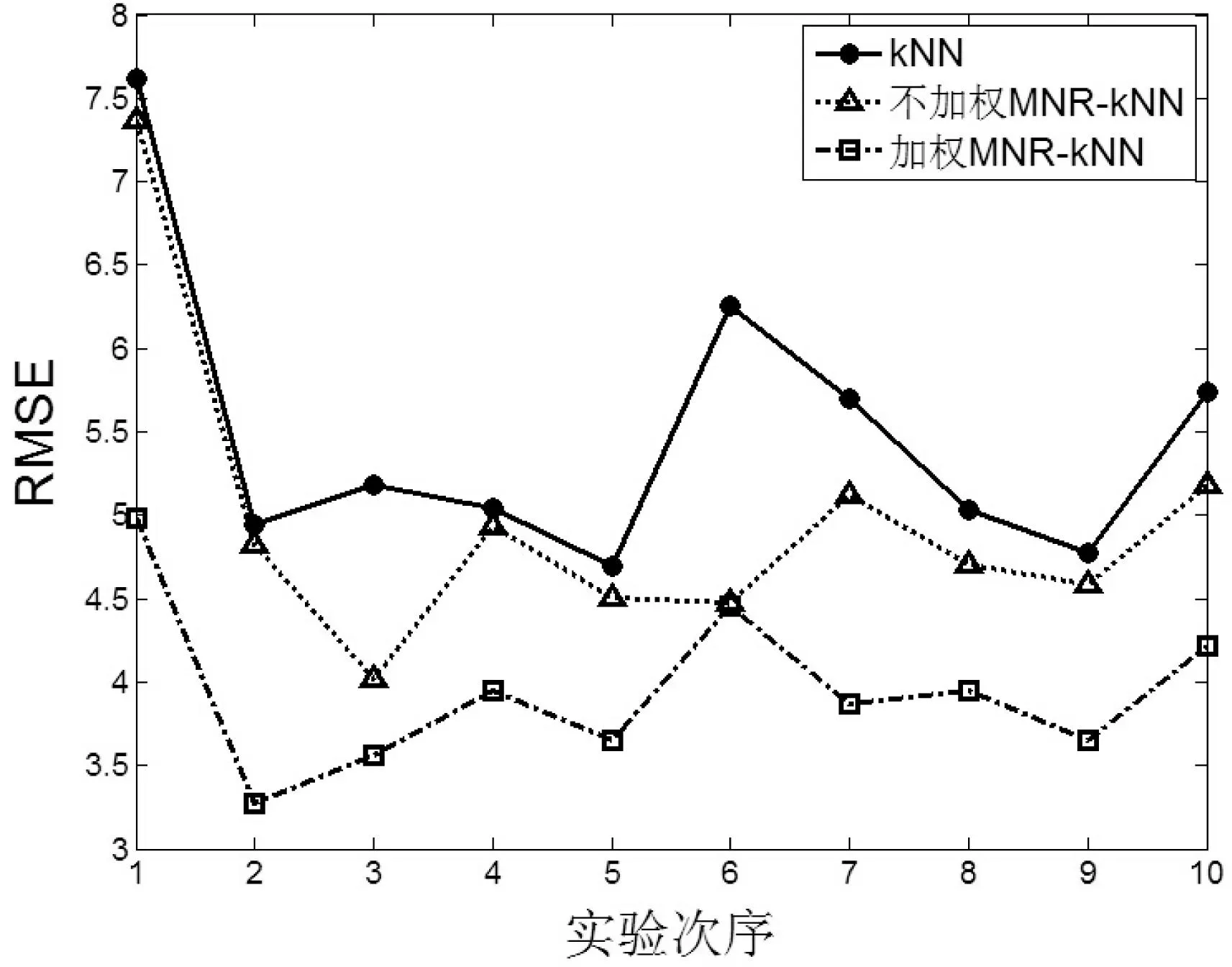
图3　数据集Housing

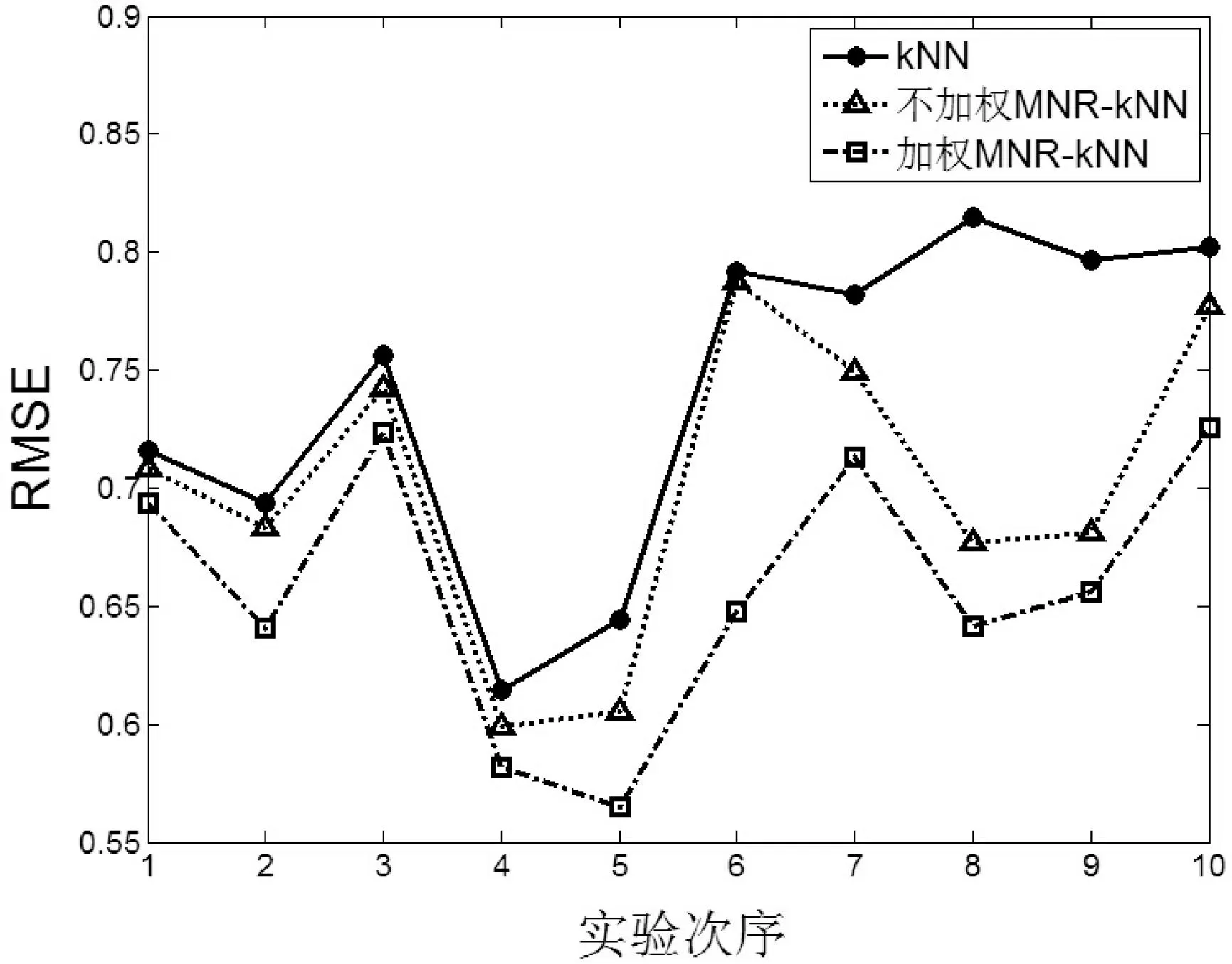
图4　数据集Winequailty

图5　数据集Mpg

图6—图9为四个数据集上的实验结果，纵坐标为CorrCoef的大小，横坐标为十次实验次序。

图6　数据集ConcreteSlump

图7　数据集Housing

图8　数据集Winequailty

图9　数据集Mpg

RMSE和CorrCoef的均值以及方差见表2和表3。

表2　RMSE均值和方差情况

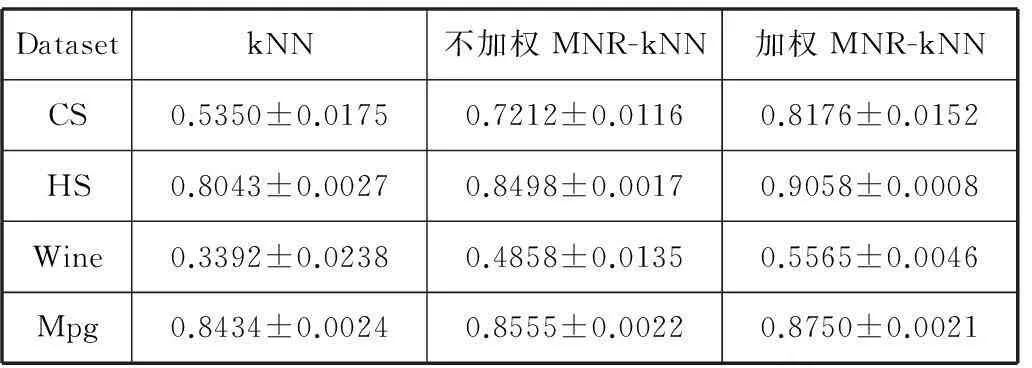
表3　CorrCoef均值和方差情况

图2-图9在四个UCI数据集上的实验显示，对于评价指标RMSE，加权MNR-kNN算法得出的RMSE均值最小，其次是不加权MNR-kNN算法，RMSE最大的是kNN算法。对于评价指标CorrCoef，总体看来，加权MNR-kNN算法得出的CorrCoef均值最大，其次是不加权MNR-kNN算法，CorrCoef最大的是kNN算法。

根据表2,对于评价指标RMSE，加权MNR-kNN算法取得的RMSE均值最小，其次分别是不加权MNR-kNN算法和kNN算法。最明显的在CS数据集上，加权MNR-kNN算法比kNN算法在评价指标RMSE均值上降低了1.936，同时不加权MNR-kNN算法也比kNN算法降低了0.8213。另外根据表3，加权MNR-kNN算法取得的相关系数均值最大，其次是不加权MMR-kNN算法和kNN算法。在CS数据集上的实验表明，加权MNR-kNN算法和不加权MNR-kNN算法比kNN算法在评价指标上CorrCoef均值上分别提高了28.26%和18.62%，改善效果显著。此外，从RMSE和CorrCoef方差总体情况来看，加权MNR-kNN算法方差最小，其次是不加权MMR-kNN算法和kNN算法。这说明本文提出的MNR-kNN算法比kNN算法算法更稳定。

因此，综合看来，加权MNR-kNN算法效果最好，其次是不加权MMR-kNN算法，效果最差的是kNN算法。这说明本文提出的MMR-kNN算法(包括加权和不加权两种情况)预测准确率更高，效果相比kNN算法也更好，同时加权MNR-kNN算法比不加权MNR-kNN算法要好。

4结语

针对kNN算法中k值固定不变问题以及如何在预测时去除噪声样本，本文提出了基于混合模重构的kNN算法(MNR-kNN)。通过l1-范数，MNR-kNN算法中k值根据样本之间相关性情况取不同的值，同时在重构过程中利用l2,1-范数去除噪声。另外根据相关性大小可将MNR-kNN算法具体分加权情况和不加权情况。实验表明，在同样的训练样本和测试样本情况下，使用三种算法进行预测，加权MNR-kNN算法效果最好，其次是不加权MNR-kNN算法，而kNN算法取得的效果不佳。

本文提出的MNR-kNN算法可以用于信号编码和压缩、降维去噪、人脸识别、文本挖掘等领域。将来可以进一步考虑如何在实际应用中降低MNR-kNN算法的时间复杂度，比如分块处理等，以此来取得相应的实际应用价值。

参考文献

[1] Qin Y S,Zhang S C,Zhang C Q. Combinining knn imputation and bootstrap calibreated:empirical likelihood for incomplete data analysis[J]. International Journal of Data Warehousing and Mining,2010,6(4):61-73.

[2] Cora G,Wojna A. A classifier combining rule induction and KNN method with automated selection of optimal neighbourhood[C]//Pr-oceedings of the 13rd European Conference on Machine Learning. London,UK: Springer-Verlag,2002:111-123.

[3] Matthieu Kowalski. Sparse regression using mixed norms[J]. Applied and Computational Harmonic Analysis, 2009,27(3):303-324.

[4] Hechenbichler K,Schliep K. Weighted k-nearest-neighbor techniques and ordinal classification,Discussion Paper 399[R]. Munich,Germ-any: Ludwing-Maximilians University Munich,2004.

[5] Wang T,Qin Z X,Zhang S C, et al. Cost-sensitive classification with inadequate labeled data[J]. Information Systems,2012,37(5):508-516.

[6] Zhang S C. Decision tree classifiers sensitive to heterogeneous costs[J]. Journal of Systems and Software,2012,85(4):771-779.

[7] Zhang S C. Cost-sensitive classification with respect to waiting cost[J]. Knowledge-Based Systems,2010,23(5):369-378.

[8] Zhu X,Zhang S,Zhang J,et al. Cost-sensitive imputing missing values ordering[J].Aaai Press,2007,2:1922-1923.

[9] 李长彬，黄东，黎永壹.局部线性重构分类算法研究[J].计算机应用与软件,2013,30(4):156-158,210.

[10] Zhu X F,Huang Z,Cheng H,et al. Sparse hashing for fast multi-media search[J]. ACM Transactions on Information System,2013,31(2):9.

[11] Zhang S C,Jin Z,Zhu X F. Missing data imputation by utilizing information within incomplete instances[J]. Journal of System and Software,2011,84(3):452-459.

[12] Zhu X F,Zhang S C,Jin Z,et al. Missing value estimation for mixed-attribute data sets[J]. IEEE Transactions on Knowledge and Engineering,2011,23(1):110-121.

[13] Zhu X F,Huang Z,Shen H T,et al. Dimensionality reduction by Mixed Kernel Canonical Correlation Analysis[J]. Pattern Recognition,2012,45(8):3003-3016.

[14] Zhu X F,Suk H,Shen D. A Novel Matrix-Similarity Based Loss Function for Joint Regression and Classification in AD Diagnosis[J]. NeuroImage,2014,100:91-105.

[15] Zhu X F,Huang Z,Shen H T,et al. Linear Cross-Modal Hashing for Effective Multimedia Search[C]//Proceedings of ACM M M,2013:143-152.

[16] Zhu X F,Huang Z,Yang Y,et al. Self-tau-ght dimensionality reduction on the high-dimensional small-sized data[J]. Pattern Recognition,2013,46(1):215-229.

[17] Zhu X F,Wu X D,Ding W,et al. Feature selection by joint graph sparse coding[C] // Proceedings of the 2013 Siam Intern-ational Conference on Data Mining,2013:803-811.

[18] UCI repository of machine learning datasets[DB/OL].[2012-01-15]. http://archive.ics.uci.edu/-ml/.

中图分类号TP181

文献标识码A

DOI:10.3969/j.issn.1000-386x.2016.02.054

收稿日期：2014-08-19。国家自然科学基金项目(61170131，61263035，61363009);国家高技术研究发展计划项目(2012AA011005);国家重点基础研究发展计划项目(2013CB329404);广西自然科学基金项目(2012GXNSFGA06004);广西研究生教育创新计划项目(YCSZ2015095，YCSZ2015096)；广西多源信息挖掘与安全重点实验室开放基金项目(MIMS13-08)。龚永红，本科，主研领域：图书情报学，数据挖掘。宗鸣，硕士。朱永华，本科。程德波，硕士。