CONVERGENCE RATE OF SOLUTIONS TO STRONG CONTACT DISCONTINUITY FOR THE ONE-DIMENSIONAL COMPRESSIBLE RADIATION HYDRODYNAMICS MODEL∗
Zhengzheng CHEN(陈正争)Xiaojuan CHAI(柴晓娟)Wenjuan WANG(王文娟)School of Mathematical Sciences,Anhui University,Hefei 230601,China
CONVERGENCE RATE OF SOLUTIONS TO STRONG CONTACT DISCONTINUITY FOR THE ONE-DIMENSIONAL COMPRESSIBLE RADIATION HYDRODYNAMICS MODEL∗
Zhengzheng CHEN(陈正争)†Xiaojuan CHAI(柴晓娟)Wenjuan WANG(王文娟)
School of Mathematical Sciences,Anhui University,Hefei 230601,China
E-mail:chenzzandu@163.com;chaixj.ahu@gmail.com;wangwenjuan@ahu.edu.cn
AbstractThis paper is concerned with a singular limit for the one-dimensional compressible radiation hydrodynamics model.The singular limit we consider corresponds to the physical problem of letting the Bouguer number in finite while keeping the Boltzmann number constant.In the case when the corresponding Euler system admits a contact discontinuity wave,Wang and Xie(2011)[12]recently veri fied this singular limit and proved that the solution of the compressible radiation hydrodynamics model converges to the strong contact discontinuity wave in the L∝-norm away from the discontinuity line at a rate of,as the reciprocal of the Bouguer number tends to zero.In this paper,Wang and Xie’s convergence rate is improved toby introducing a new a priori assumption and some re fined energy estimates.Moreover,it is shown that the radiation fl ux q tends to zero in the L∝-norm away from the discontinuity line,at a convergence rate as the reciprocal of the Bouguer number tends to zero.
Key wordsradiation hydrodynamics model;singular limit;contact discontinuity;convergence rate;energy estimates
2010 MR Subject Classi fi cation35L65;58J45
∗Received September 15,2014;revised May 25,2015.This work was supported by the Doctoral Scienti fi c Research Funds of Anhui University(J10113190005)and the Tian Yuan Foundation of China(11426031).
†Corresponding author:Zhengzheng CHEN.
1 Introduction
The compressible radiation hydrodynamics model that governs the motions of the one-dimensional radiating gas can be written in the Lagrangian coordinates as(see[1-6])
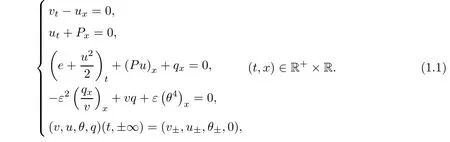
here the unknown functions are the speci fi c volume v>0,the velocity u,the absolute temperature θ>0,the internal energy e,the pressure P and the radiation fl ux q of the fluids respectively.The parameter ε>0 represents the reciprocal of the Bouguer number,and v±>0,u±and θ±are given constants.For the derivation and physical meaning of ε,we refer to[5,6]for details.
In the ideal fluids,i.e.,ε=0,system(1.1)is reduced to the compressible Euler system:
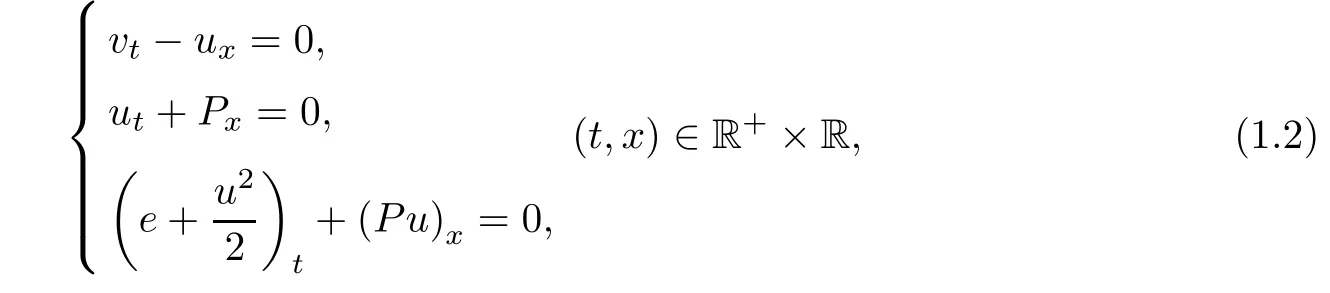
which is a strict hyperbolic system of conservation laws.The Riemann problem of system(1.2)admits some basic wave patterns:the shock wave,rarefaction wave,contact discontinuity and some linear combinations of them,called the Riemann solution.
We are concerned with the limiting process of the the radiation hydrodynamics flows when ε tends to zero and expect that the solution of(1.1)will approach to the Riemann solution of the Euler system(1.2)in such a process.This problem has been recently studied by some authors with signi fi cant progress.In[12],Wang and Xie first considered the singular limit to a single contact discontinuity and proved that the smooth solution of system(1.1)tends to the strong contact discontinuity solution of(1.2)as ε→0.Moreover,a convergence rateis obtained in[12].The main difficulty they encounter lies in deducing the suitable a priori estimates for solutions of(1.1)because the system is much less dissipative.To achieve those,they use a direct but trick energy analysis.Then using some similar ideas as[12],Rohde,Wang and Xie[13]considered the singular limit to the supposition of rarefaction waves and contact discontinuity for system(1.1)with a slower convergence rate
A natural and interesting problem is that whether the convergence rates established in[12,13]can be improved further?The main purpose of this paper is devoted to this problem and as a first step,we consider the same problem as[12]and focus our attention on improving the convergence rate.By introducing a new a priori assumption(2.6)and some re fined energy estimates,we obtain a faster convergence rate ε78,instead of ε1
4received in[12].
Now we begin to formulate our main result.In the present paper,we consider the ideal polytropic fluids so that P and e are given by
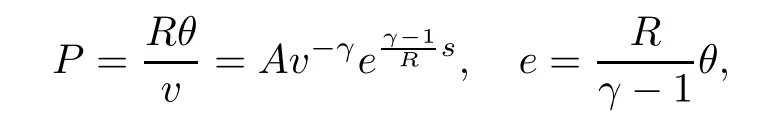
where γ>1 is the adiabatic exponent,s is the entropy and A,R are two positive constants.We impose(1.2)with the following Riemann initial data
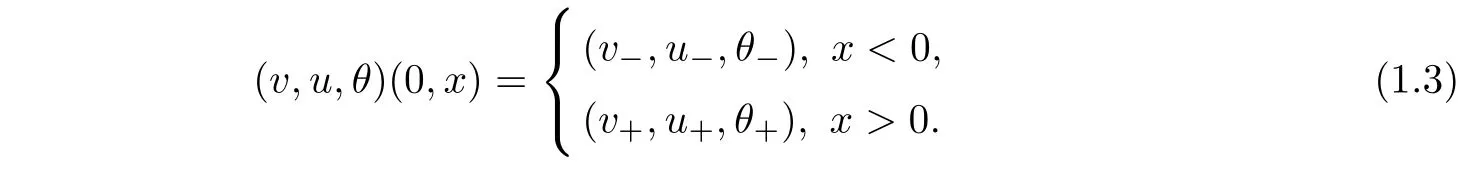
It is known that the contact discontinuity solution of the Riemann problem(1.2)-(1.3)takes the form[8,9]
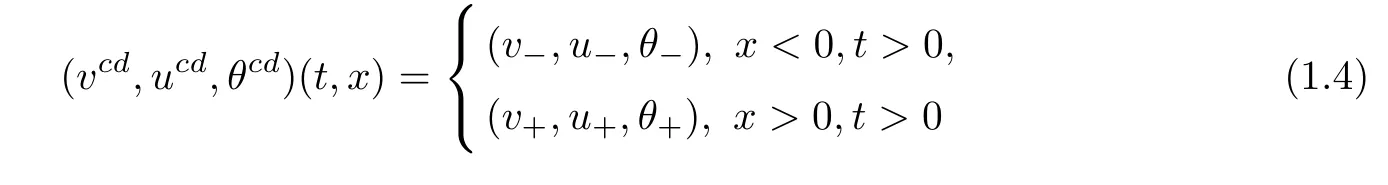
provided that

In the setting of the compressible radiation hydrodynamics model(1.1),the corresponding wave to the contact discontinuity becomes smooth and behaves as a di ff usion wave due to the radiation effect.We call this wave a“viscous contact wave”.As[13],we construct the viscous contact waveas follows.Motivated by(1.5),the pressure of the profileis expected to be almost constant,that is

And the radiation fl ux Q is expected to act a di ff usion term

Then the energy equation(1.1)3is approximated by
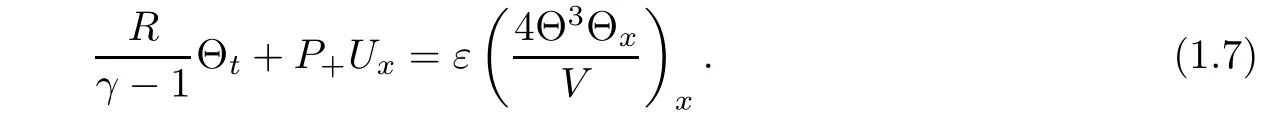
Using equations(1.6),(1.7)and Vt=Ux,we get a nonlinear di ff usion equation

which has a unique self-similarity solutiondue to[10,11,34].Furthermore,Θ(ξ)is a monotone function,increasing if θ+>θ−and decreasing if θ+<θ−.On the other hand,there exists some positive constant,such that for δ=|θ+−θ−|≤,Θ satisfies
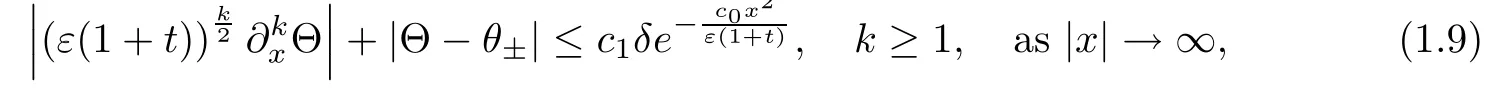
where c0and c1are two positive constants depending only on θ−andOnce Θ is determined,the viscous contact wave profileis defined as follows:

It is easy to check that the viscous contact wavesatisfies
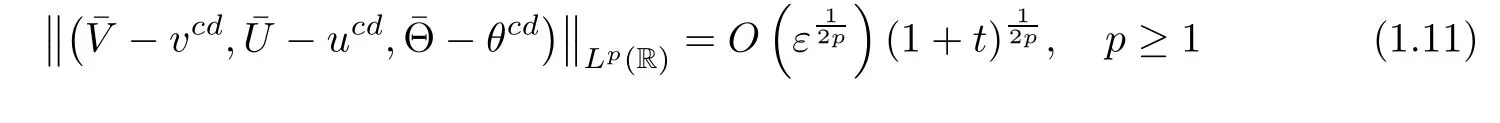
and
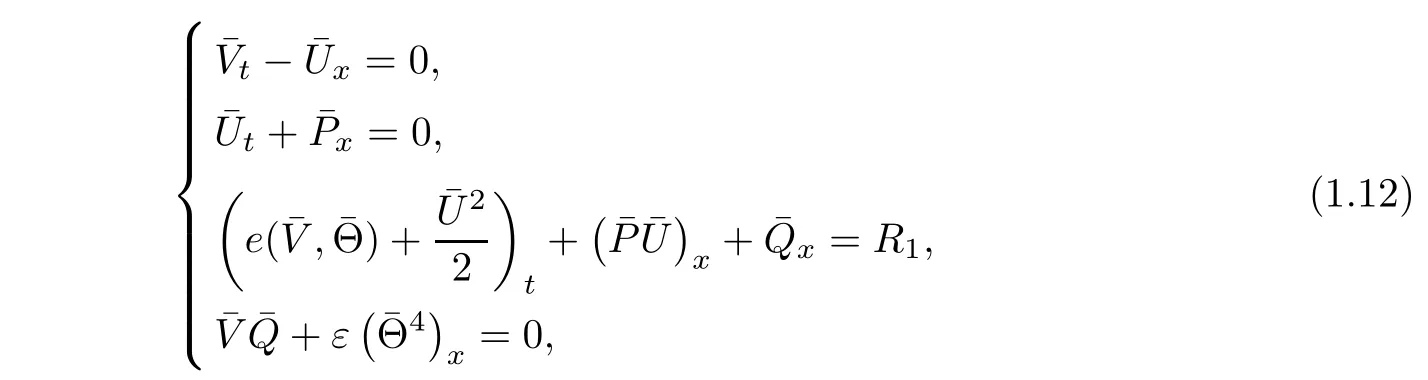

Our main result is stated as follows.
Theorem 1.1For any given(v−,u−,θ−),suppose that(v+,u+,θ+)satisfies(1.5).Let(vcd,ucd,θcd)be the contact discontinuity solution de fined in(1.4)for the Riemann problem(1.2)-(1.3).Then for any given large time T>0 and small constant σ>0,there exists a small constant ε0>0 such that for any ε∈(0,ε0),system(1.1)with the same initial data as those of(¯V,¯U,¯Θ)admits a unique smooth solution(vε,uε,θε,qε)in[0,T]×R,still denoted by(v,u,θ,q).Moreover,it holds that

where C>0 is a constant independent of ε.
Remark 1.2In Theorem 1.1,we only require the strength of the contact discontinuity to be finite and have no need to restrict it to be small.
Remark 1.3Although the convergence rate in(1.14)is the same as that in[12],we can show in(4.3)below that

Notice that(1.17)and(1.15)obviously improve the corresponding ones obtained in[12].Moreover,(1.16)is essentially new compared with the former results.
Remark 1.4A similar argument can be applied to study the singular limit for the 1-D compressible radiation hydrodynamics model to the superposition of rarefaction waves and contact discontinuity,and thus improves the main result of[13].
Now we outline the main ideas used in proving our main result.The faster convergence rateobtained in(1.15)is essentially due to two factors.One is the ansatzde fined(1.10),which was first used in[13]for the study of the singular limit for the 1-D compressible radiation hydrodynamics model to the superposition of rarefaction waves and contact discontinuity.This ansatz satisfies the mass equation and the momentum equationexactly,while the error terms occur only in the energy and radiation equations.Notice that the error term R1is higher order in ε than the corresponding one de fined in[12]and thus leads the convergence to become faster.The other one,which is also the main novelty of this paper,is the new a priori assumption de fined in(2.6)below.To state our argument clearly,let’s recall that the analysis in[12]is to perform some energy estimates based on the a priori assumption that


We observe that the first termin the right hand of(1.20)can be improved to Cε by some more elaborate energy estimates.Moreover,if we drive the energy estimates under the a priori assumption that
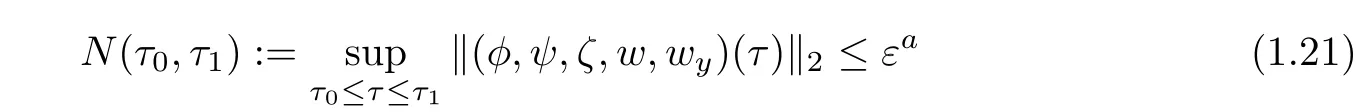
with a>0 being a positive constant to be determined later,then the estimates(1.19),(1.20)with the termreplaced by Cε andstill hold by the smallness of ε,thus we obtain thatwithrespectively.Then by the Sobolev inequality,the convergence rate for‖(φ,ψ,ζ)(τ)‖L∝is improved toFurthermore,one can prove that‖(φyy,ψyy,ζyy)(τ)‖2≤ Cεθwithand consequently,the norm N(τ0,τ1)de fined in(1.18)can be bounded byand thus the a priori assumption(1.21)is indeed true by choosing a to be some positive constant smaller thanand ε>0 sufficiently small.
Based on the above observations,we choose the new a priori assumption(2.6)in this paper.Such type a priori assumption is first used in[26]for the study of vanishing viscosity limit torarefaction wave with vacuum for the 1-D compressible Navier-Stokes equations.However,unlike the case of the zero dissipation limit to rarefaction wave[26,27,35],the a priori assumption(2.6)can indeed improve the convergence rate for solutions of the 1-D compressible radiation hydrodynamics model toward the contact discontinuity.We remark that the method of this paper can also be applied to study the zero dissipation limit to contact discontinuity for the 1-D compressible Navier-Stokes equations and thus improves the main results obtained in[17,18].
Before concluding this section,we point out that there have been extensive studies on the compressible radiation hydrodynamics model and related models.Kawashima and Nishibata[6]studied a singular limit for a certain class of hyperbolic-elliptic coupled systems which contains a compressible radiation hydrodynamic system as a typical example.They shown that the solution to the hyperbolic-elliptic coupled system converges to the solution of the corresponding hyperbolic-parabolic coupled system with a convergence rate.In[24],Lattanzio and Marcati considered both the hyperbolic-parabolic and the hyperbolic-hyperbolic relaxation limits for the scalar Hamer model[7],which is the third order approximation of system(1.1).The results in[24]were later generalized by Francesco[33]to multidimensional case.For more interesting results on the Hamer model,we refer to[19-23,28,29]and the references therein.We should note that the existence and nonlinear stability of the basic waves for the compressible radiation hydrodynamics model has been studied extensively,we refer to[1,2,25,32]for the existence and nonlinear stability of shock profiles,[14-16]for the stability of contact discontinuity wave,and[30,31]for the stability of rarefaction wave.
The reminder of this paper is organized as follows.After stating some notations,in Section 2,we will reformulate our problem into a perturbation one near the viscous contact wavede fined in(1.10).Section 3 is devoted to deducing the a priori estimates for solutions to the Cauchy problem(2.4).Finally,the proof of our main Theorem 1.1 is given in Section 4.
NotationsThroughout this paper,for simplicity,we will omit the variables t,x of functions if it does not cause any confusion.C denotes a generic constant which may vary in different estimates.If the dependence need to be explicitly pointed out,the notations Ci(i∈N)are used.Hl(R)denotes the usual l-th order Sobolev space with its norm
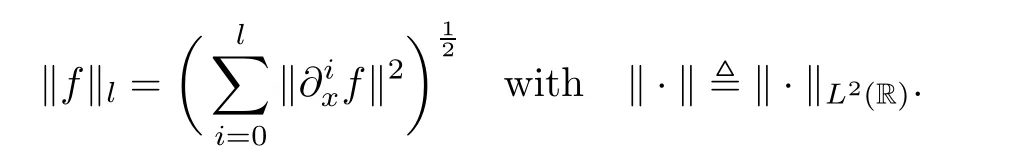
2 Reformulation of the Problem
This section is devoted to reformulating our original problem.Due to estimates(1.9)and(1.11),to prove the main theorem,it suffices to show that there exists a solution to(1.1)in a neighborhood of the viscous contact waveand the asymptotic behavior of the solution to(1.1)is given byfor small parameter ε.Suppose that(v,u,θ,q)is the solution of system(1.1)with the following initial data:

De fi ne
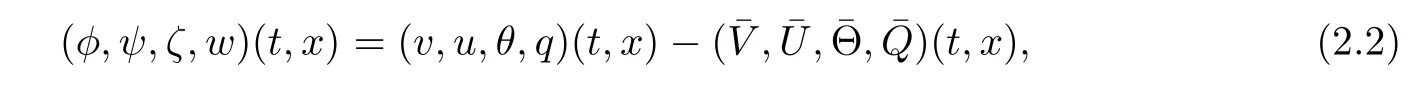
then we deduce from(1.1),(1.12)and(2.1)that

Using the following scalings:
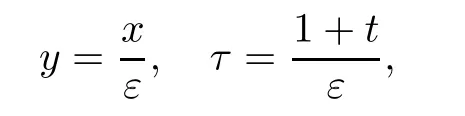
then problem(2.3)is reformulated as
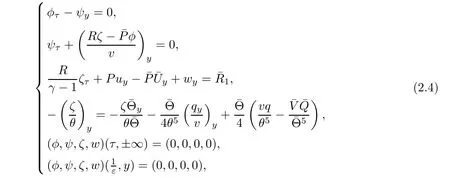

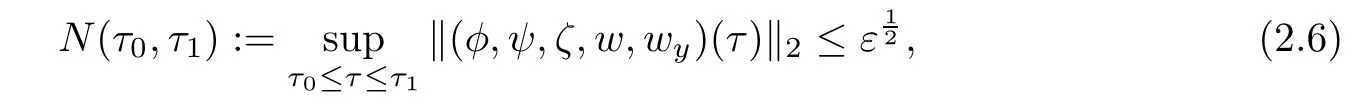
which will be achieved in the sections followed.In what follows,we seek the solutions to problem(2.4)in the following function space:

for some τ∈[τ0,τ1].
3 A Priori Estimates
In this section,we establish the a priori estimates for solutions of the Cauchy problem(2.4).
Proposition 3.1(A priori estimates)Under the assumptions of Theorem 1.1,suppose that(φ,ψ,ζ,w)∈X[τ0,τ2]is a solution of the Cauchy problem(2.4)for some τ0<τ2≤τ1,and satisfies the a priori assumption(2.6),then there exist positive constants ε0≪1 and C0which are independent of ε and τ2,such that for 0<ε<ε0,it holds that
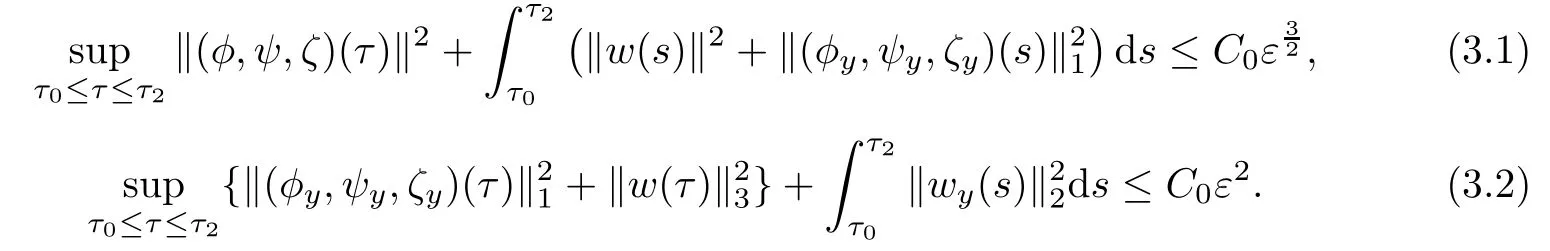
Proposition 3.1 can be obtained by a series of lemma below.Before proving the a priori estimates(3.1)-(3.2),we have from the a priori assumption(2.6)and the Sobolev inequality

that
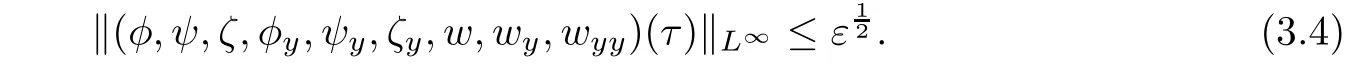
Furthermore,by the smallness of ε,we have
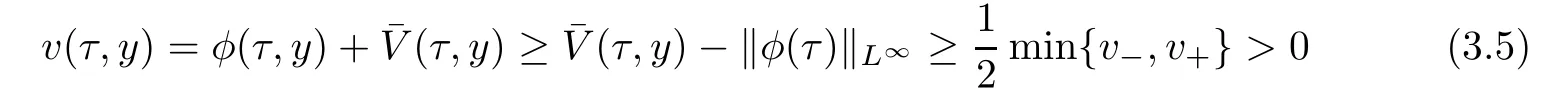
and
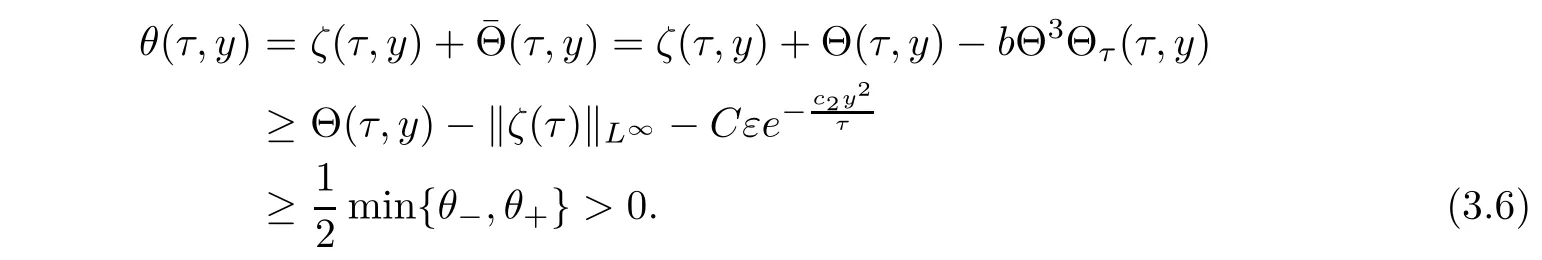
With(3.5)-(3.6)in hand,we now give the L2-estimates on(φ,ψ,ζ)(τ,y).
Lemma 3.2Under the assumptions of Proposition 3.1,if ε is suitably small,then there exists a positive constant C>0 such that
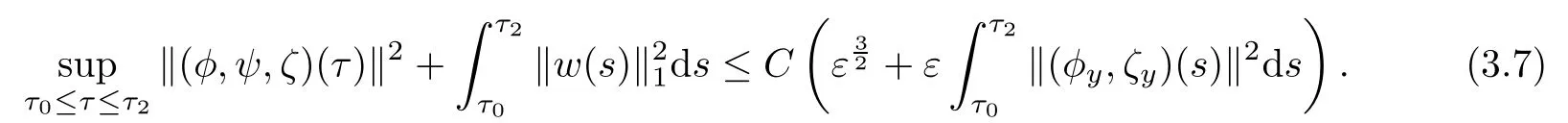
ProofSimilar to[12],we have
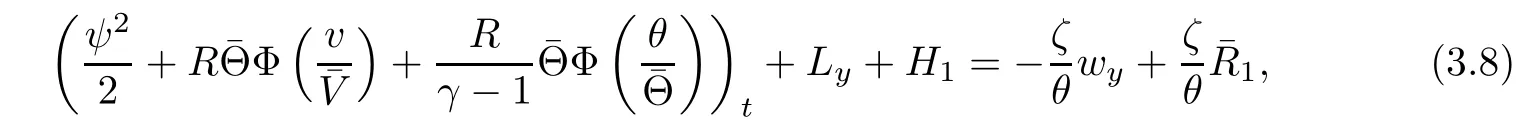
where

On the other hand,multiplying(2.4)4by w,we get by a direct computation that
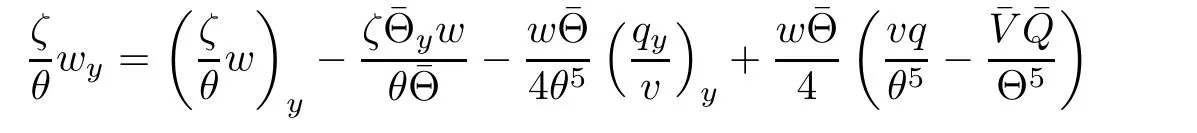
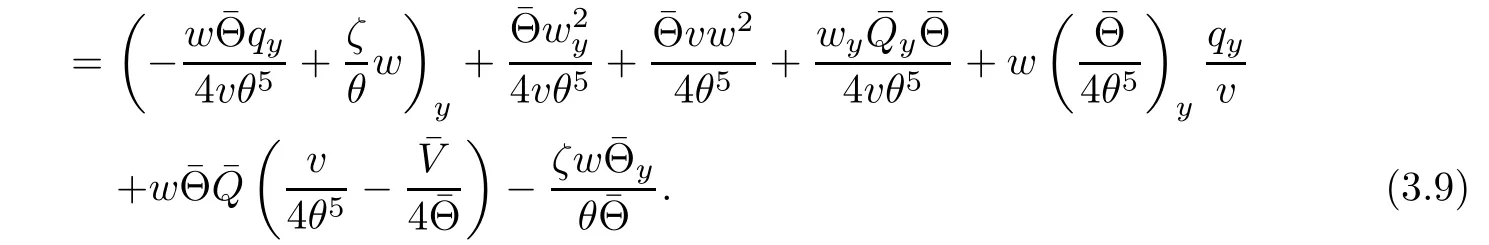
Notice that Φ(1)=Φ′(1)=0 and Φ′′(s)>0,there exists positive constants C1and C2such that
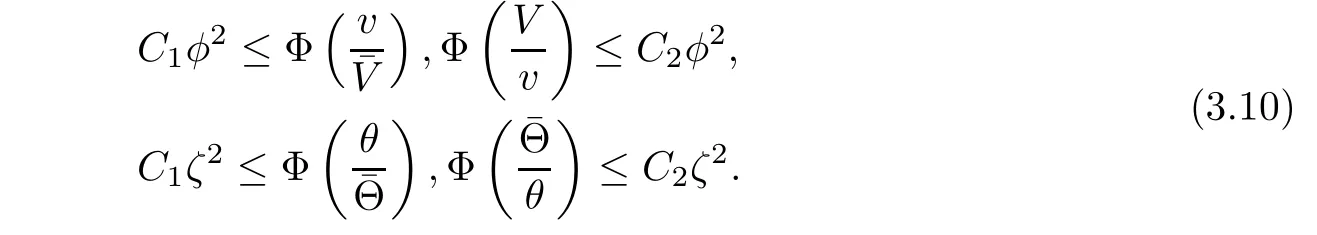
Putting(3.9)into(3.8)and integrating the resultant equation in τ and y over[τ0,τ]×R,we have from(3.10)that
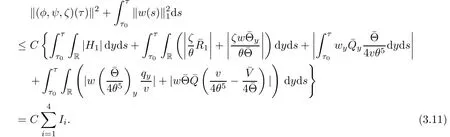
Now we estimate the terms Ii,i=1,2,3,4 one by one.It follows from(2.5)1and the Cauchy inequality that
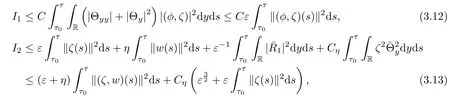
here and hereafter,η>0 denotes a suitably small constant and Cη>0 denotes a constant depending on η.
Using integration by parts,(1.10),(2.5)1,(3.4)and the Cauchy inequality,we have
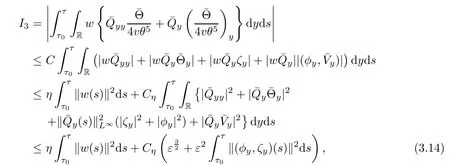
and

Combining(3.11)-(3.15),we get by the smallness of ε and η that
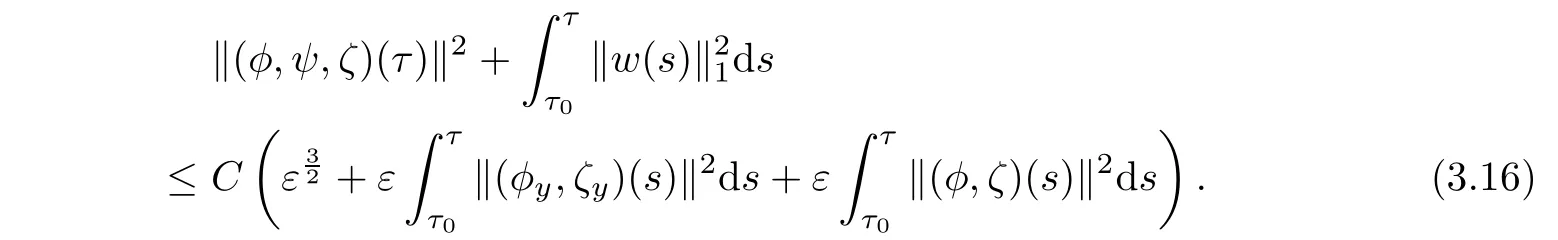
Then Gronwall’s inequality implies that
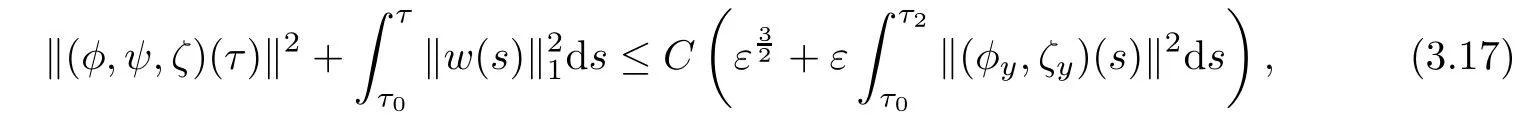
which yields(3.7)immediately.This completes the proof of Lemma 3.2.
Next,we estimate‖(φy,ψy,ζy)(τ)‖2.
Lemma 3.3Under the assumptions of Proposition 3.1,there exists a positive constant C>0 such that
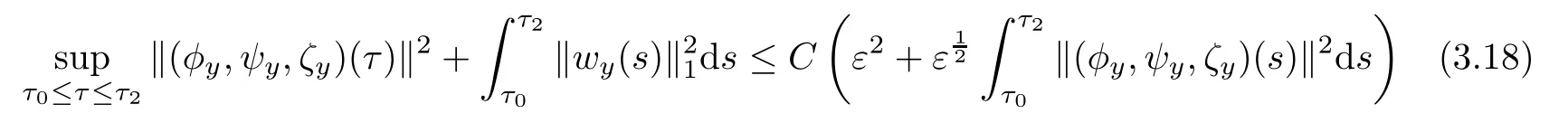
provided that ε is suitably small.
ProofLet S=(v,u,θ),then system(1.1)1,2,3can be rewritten in the following symmetric form
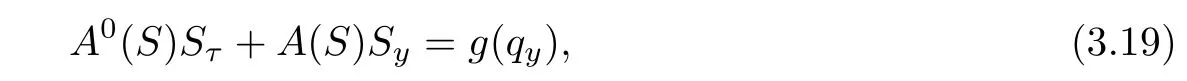
where g(qy)=(0,0,−qy)⊤and

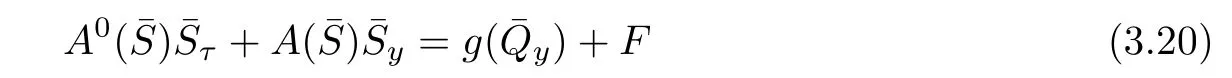
Set W=S−¯S=(φ,ψ,ζ)(τ,y),it follows from(3.19)and(3.20)that
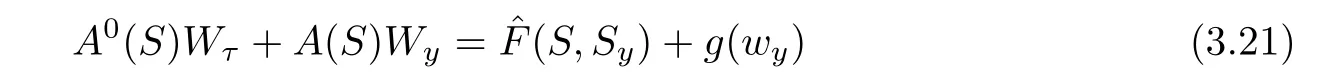
with
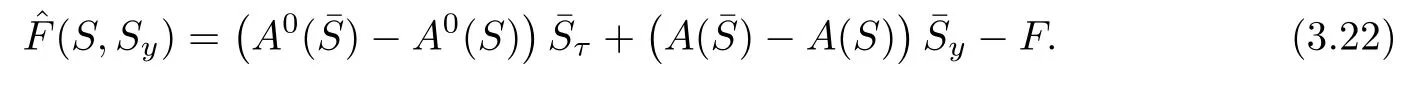
Multiplying(3.21)by A0(S)−1and differentiating the resulting equation with respect to y,then multiplying the resultant equation by(Wy)⊤A0(S),we obtain by a direct calculation that
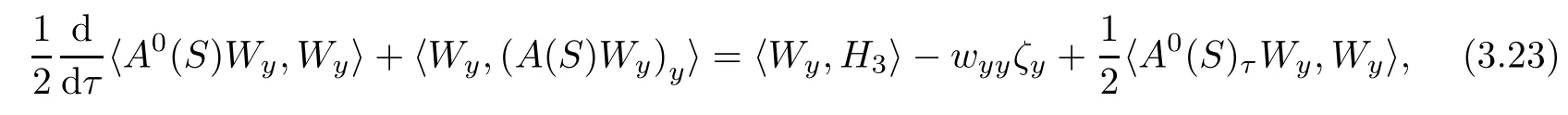
here〈·,·〉denotes the usual inner product on R3and
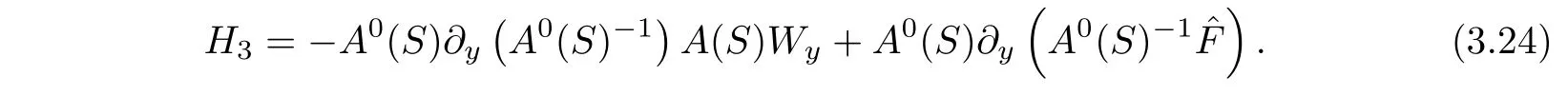
On the other hand,we rewrite equation(2.4)4as

Multiplying(3.25)by wyyyields
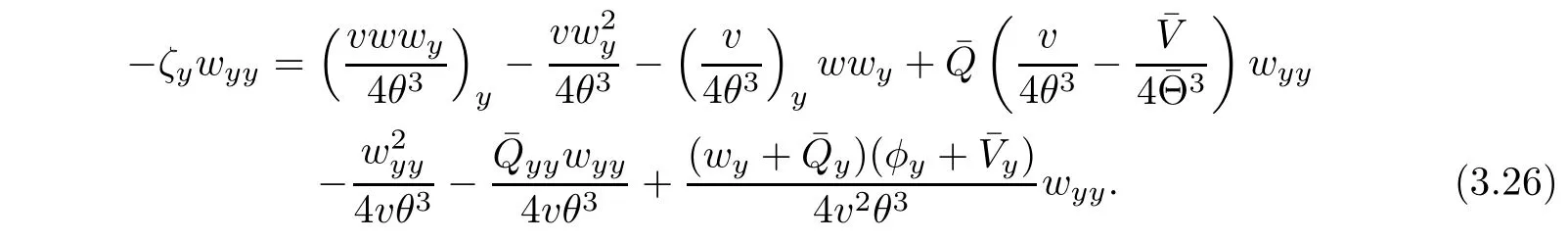
Combining(3.23)with(3.26),and integrating the resulting equation in τ and y over[τ0,τ]× R,we have

Now we estimate Ii,i=6,7,8 term by term.It follows from integration by parts,(2.5)1and(3.4)that
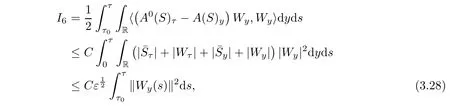
where we have used the fact that

due to(3.20)and(3.21),respectively.
For I7,we have
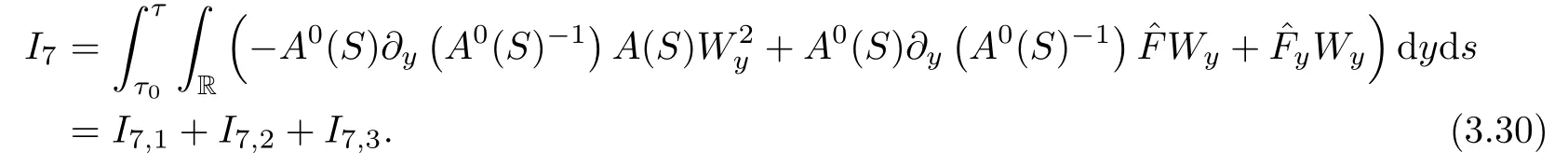
Similar to the estimate of I6,we have
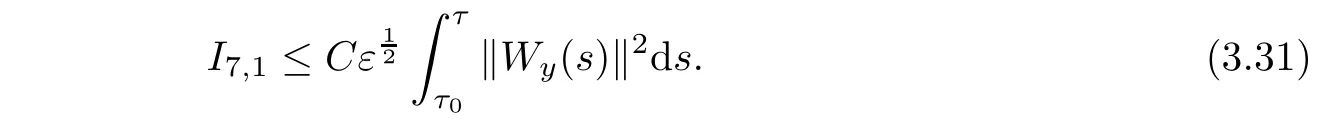
We deduce from(2.5)1,(3.22)and(3.29)that
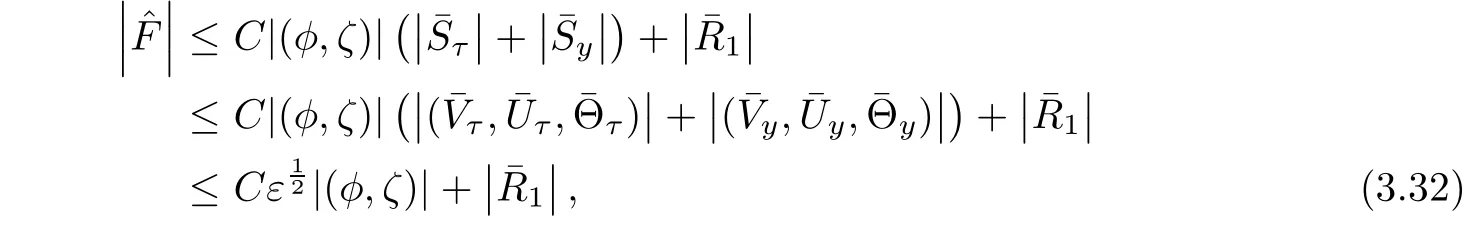
thus

Similarly,
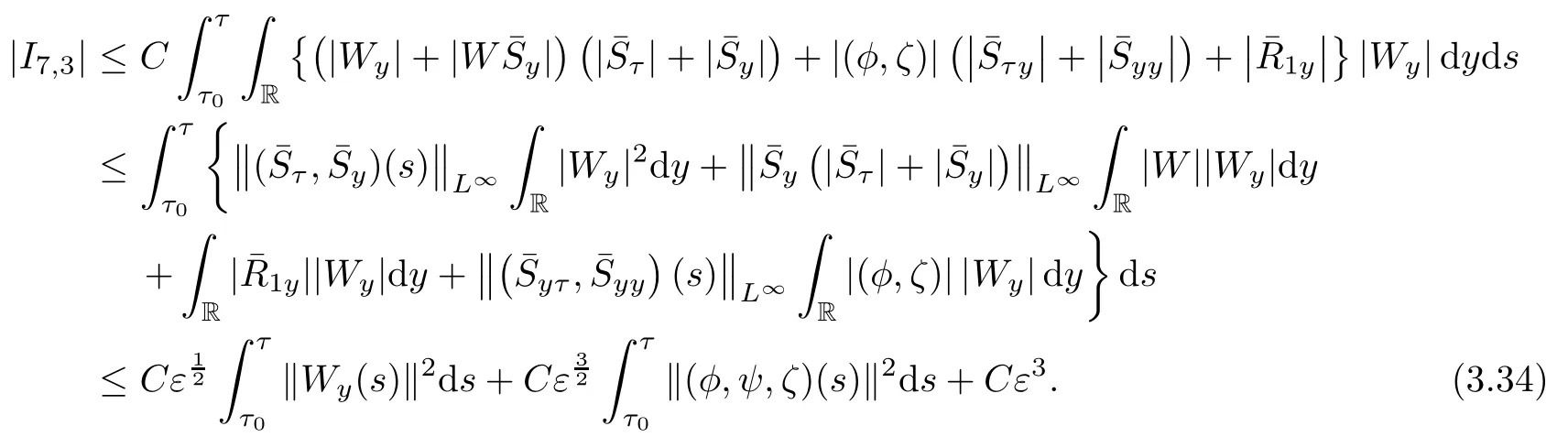
Combining(3.31),(3.33)and(3.34),we obtain
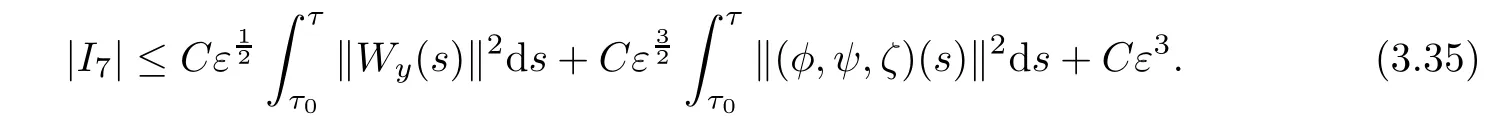
For I8,we deduce from integration by parts that

Similar to the estimates as above,can be estimated as follows
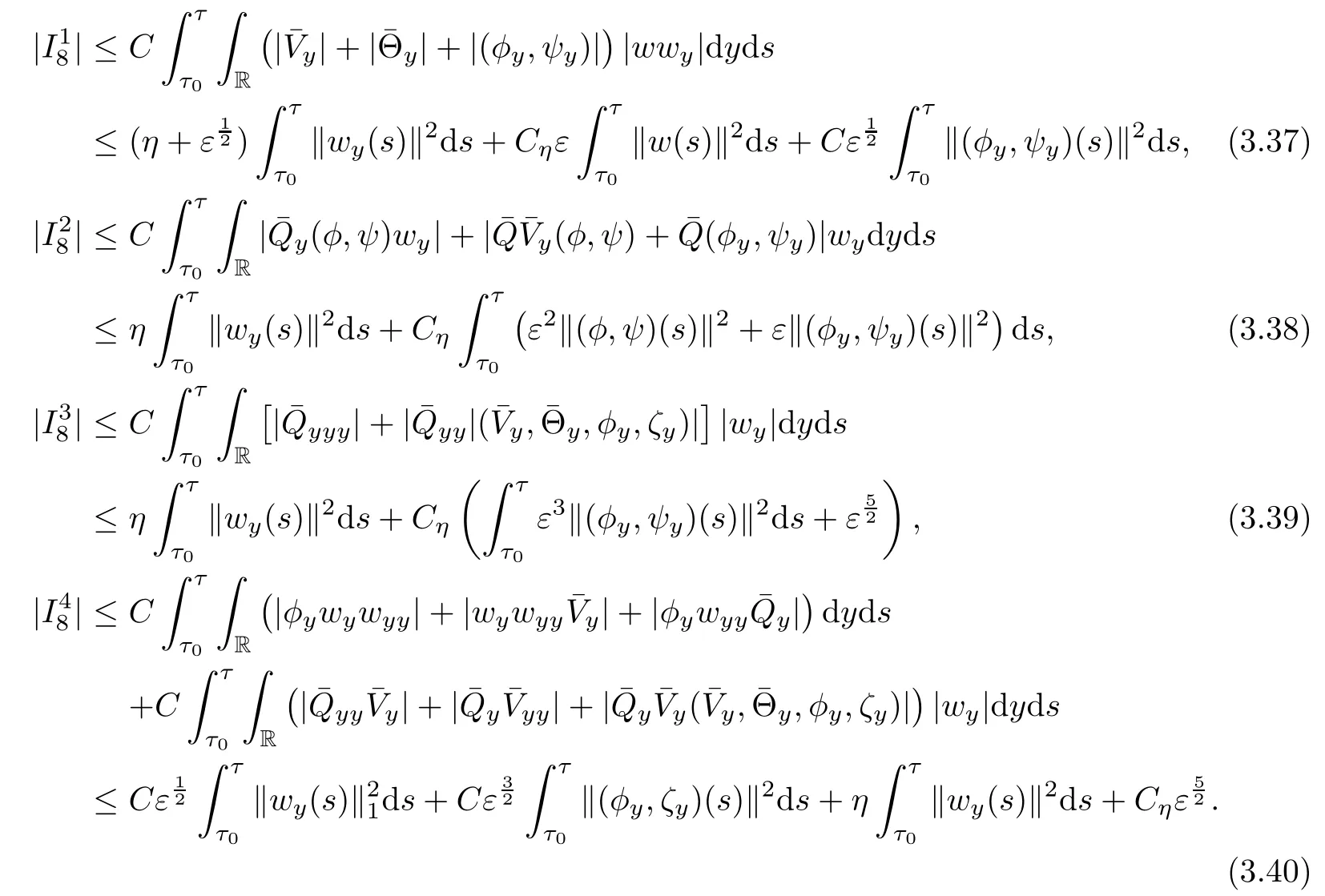
Thus it follows from(3.36)-(3.40)that
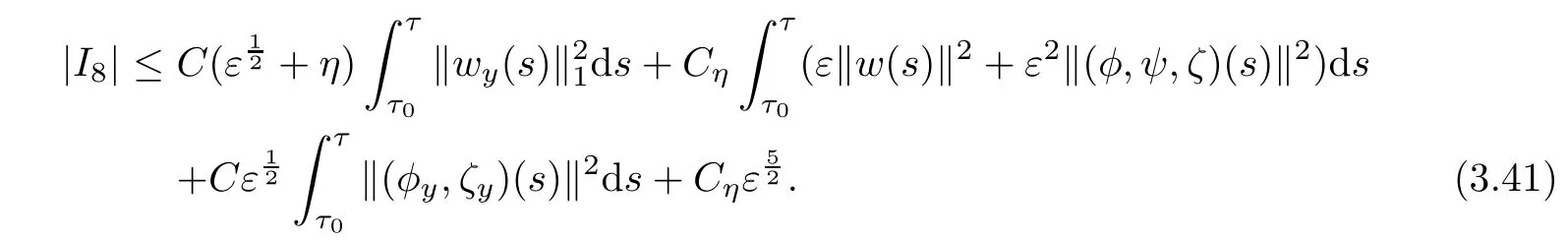
Substituting(3.28),(3.35)and(3.41)into(3.27),we have by(3.5)-(3.6),Lemma 3.2 and the smallness of ε and η that
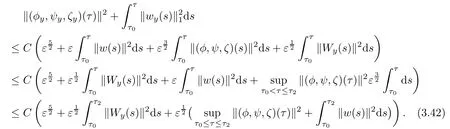
Then(3.18)follows immediately by combining(3.42)and(3.7).This completes the proof of Lemma 3.3.
To close the a priori estimates,we control the termin the following
Lemma 3.4Under the assumptions of Proposition 3.1,there exists a positive constant C>0 such that

provided that ε is suitably small.
ProofWe rewrite equations(2.4)2and(2.4)3as

Linearizing(3.44)around the viscous contact waveyields
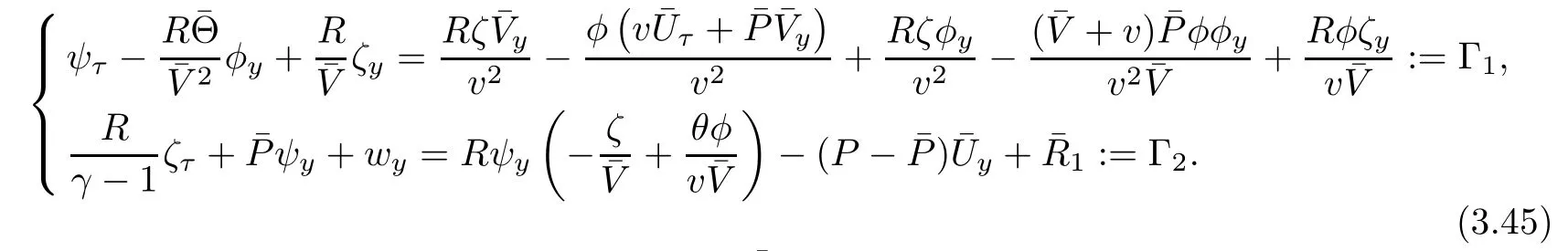
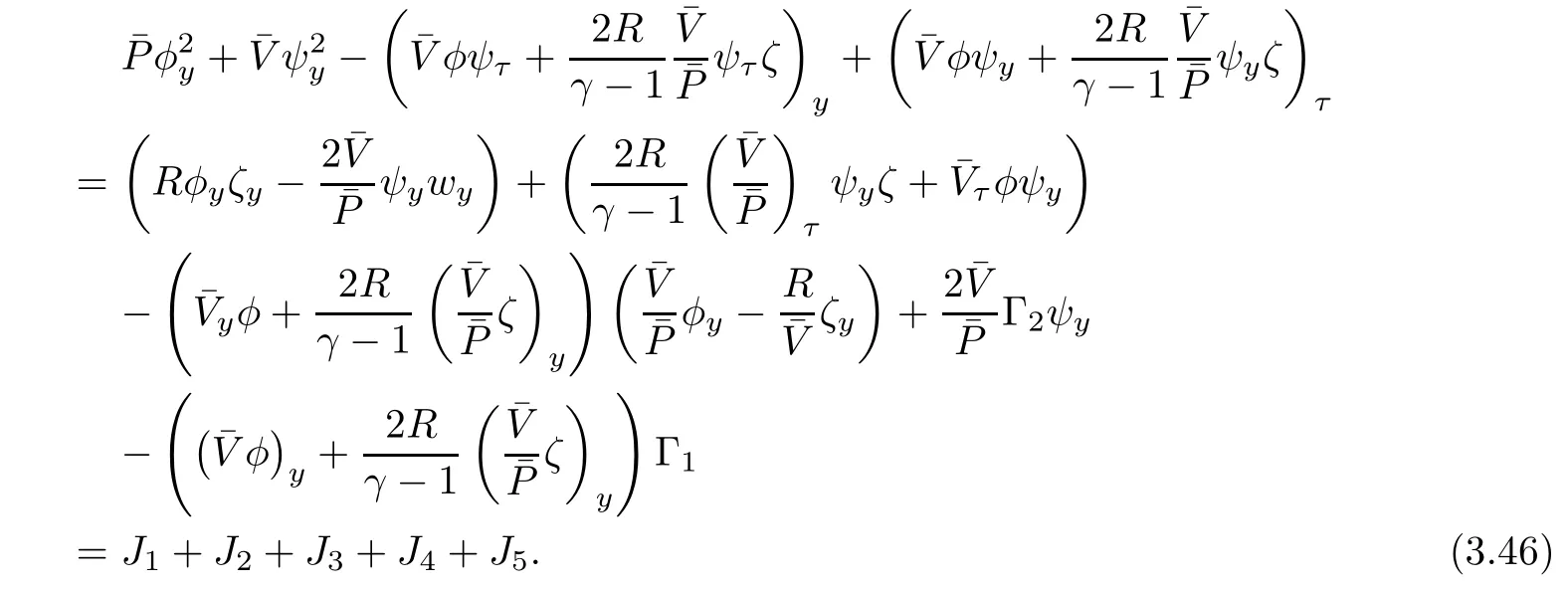
Integrating(3.46)in τ and y over[τ0,τ2]×R gives rise to
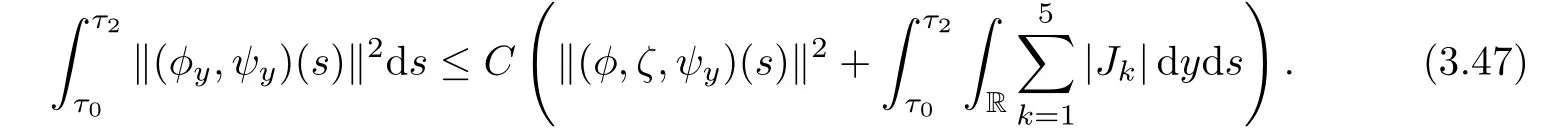
Now we estimate Ji,i=1,2,3,4,5 respectively.First,we deduce from(2.5)1and the Cauchy inequality that
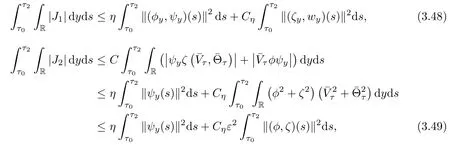
where in the last inequality of(3.49),we have used the fact that
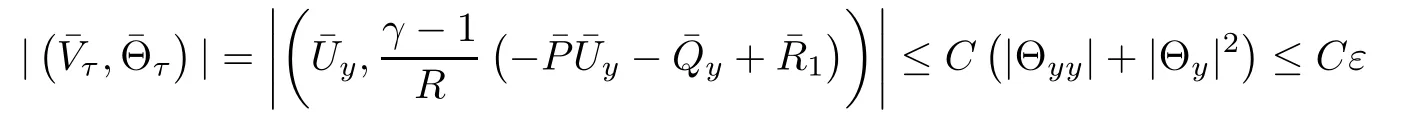
due to(2.5)1.Using the Cauchy inequality,(2.5)1and Lemma 3.2,we obtain
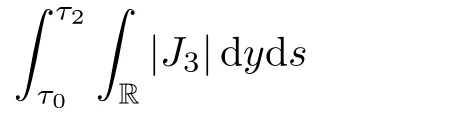
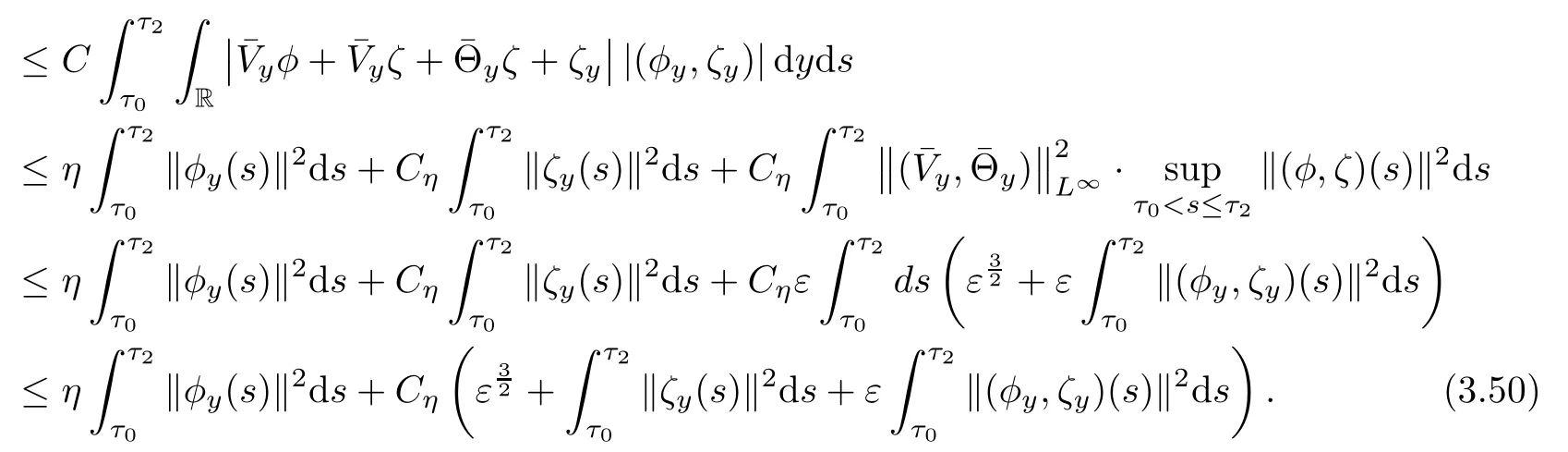
Similarly,it holds
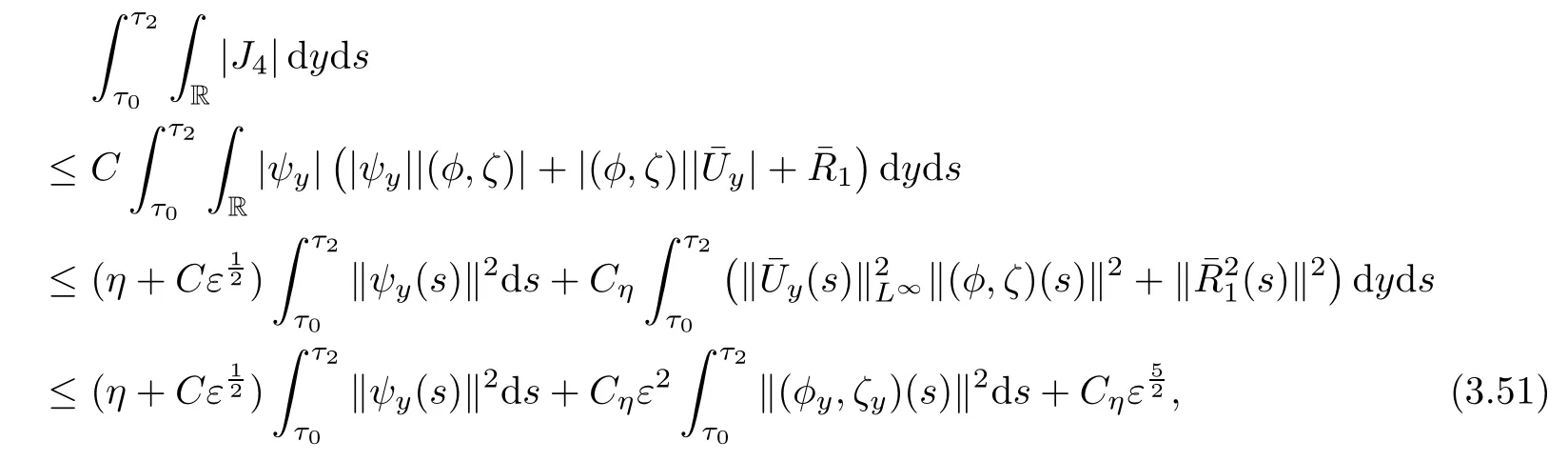
and
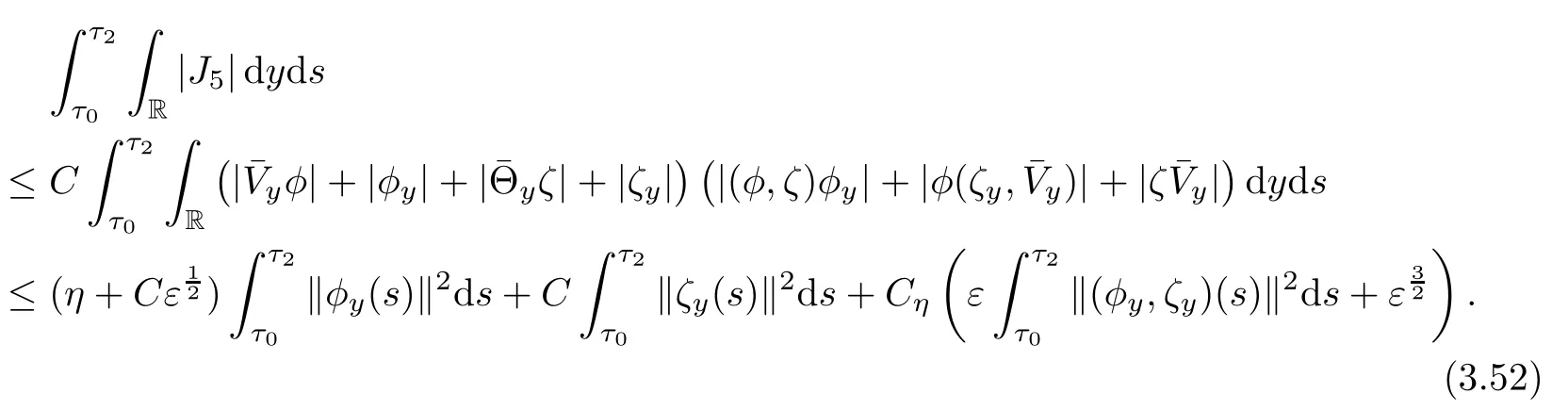
Combining(3.47)-(3.52),using Lemmas 3.2-3.3 and the smallness ε and η,we get
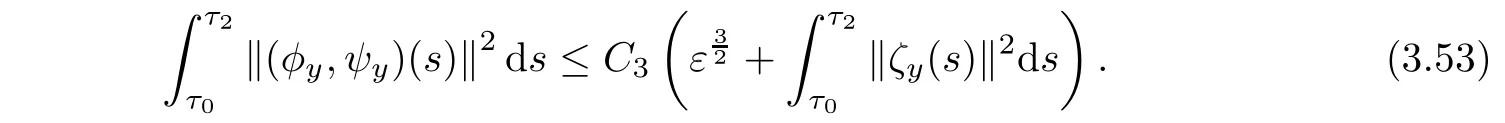
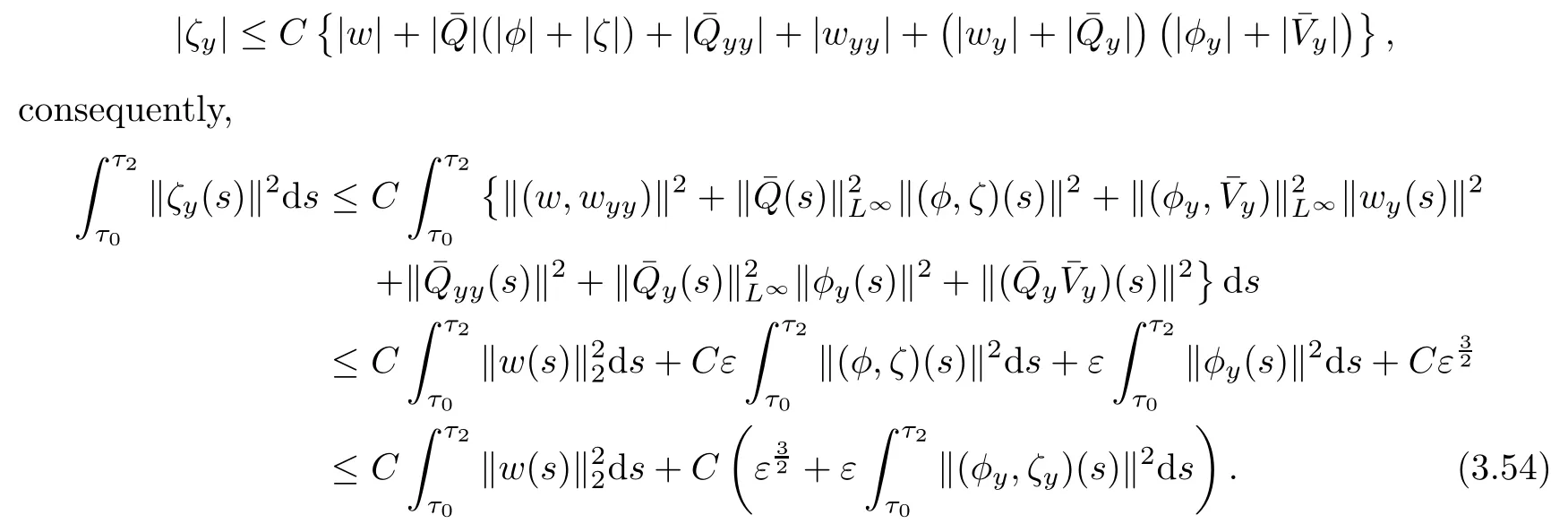
Multiplying(3.54)by 2C3and adding the resultant equation to(3.53),using Lemmas 3.2-3.3 and the smallness ε,we can get(3.43).This completes the proof of Lemma 3.4.
As a consequence of Lemmas 3.2-3.4,we have
Corollary 3.5Under the assumptions of Proposition 3.1,there exists a positive constant C>0 such that
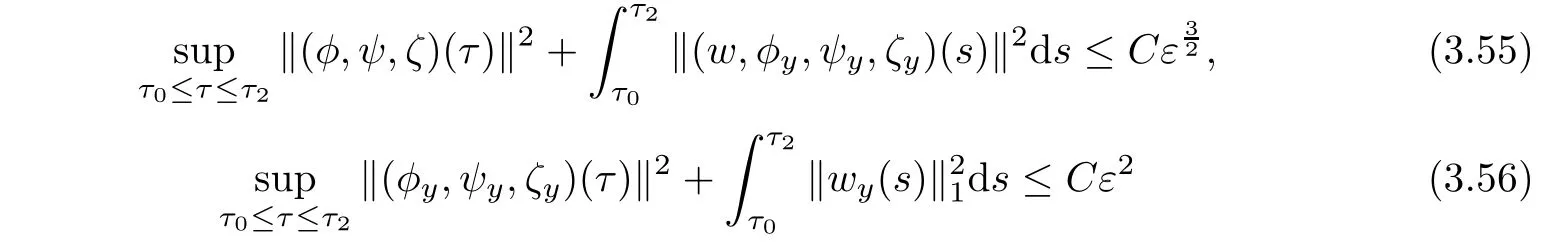
provided that ε is suitably small.
Lemma 3.6Under the assumptions of Proposition 3.1,there exists a positive constant C>0 such that for all τ∈[τ0,τ2],

provided that ε is suitably small.
ProofWe rewrite equation(2.4)4as
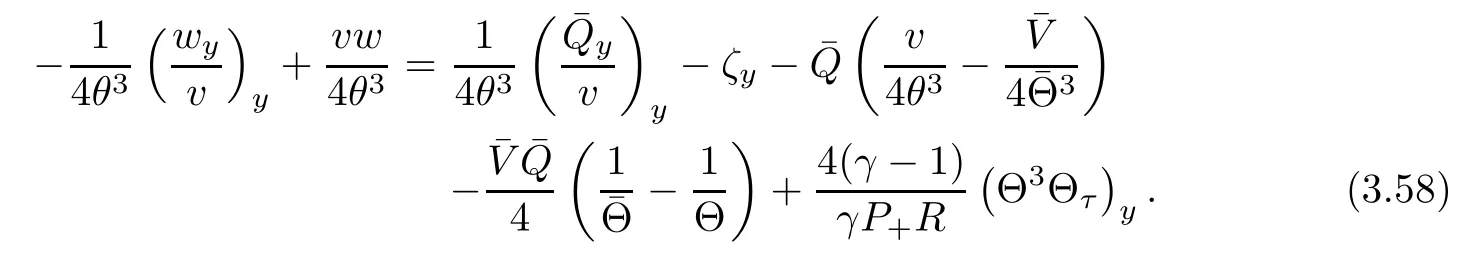
Multiplying(3.58)by w and integrating the resultant equation in y over R,we have from integration by parts that

Using the smallness of η and ε,and Corollary 3.5,we obtain
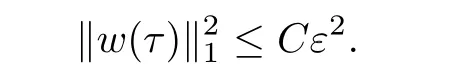
Then it follows from(3.58)that
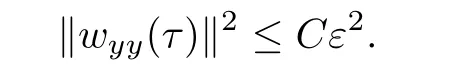
Therefore we have(3.57)holds.This completes the proof of Lemma 3.6.
By repeating the same argument,we can also obtain
Lemma 3.7Under the assumptions of Proposition 3.1,there exists a positive constant C>0 such that

provided that ε is suitably small.
Proof of Proposition 3.1Proposition 3.1 follows immediately from Corollary 3.5 and Lemmas 3.6-3.7.
4 Proof of Main Result
Now,we are ready to prove our main result as follows.
Proof of Theorem 1.1Since Proposition 3.1 is proved,we can close the a priori assumption(2.6)by choosing ε in(3.1)-(3.2)sufficiently small.Then by the standard continuity argument,one can extend the local-in-time solution to the time τ=τ1.Moreover,estimates(3.1)-(3.2)hold for τ2=τ1,that is
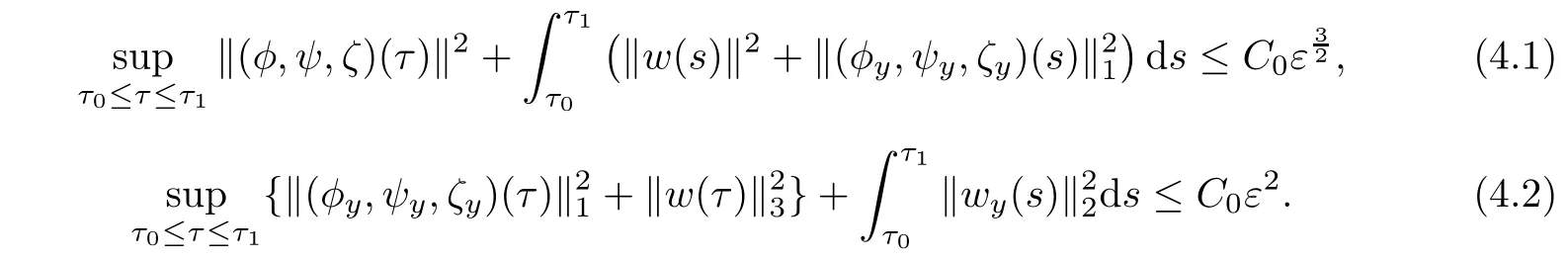
Thus
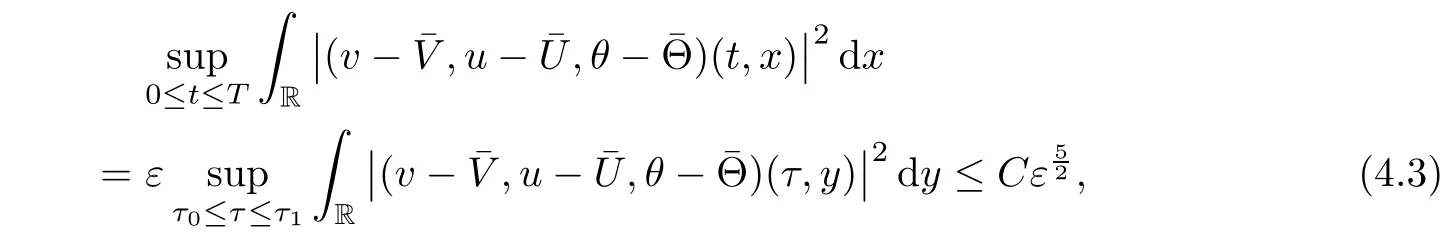
which together with(1.11)gives(1.14).Moreover,by the Sobolev inequality(3.3)and(4.1)-(4.2),we have
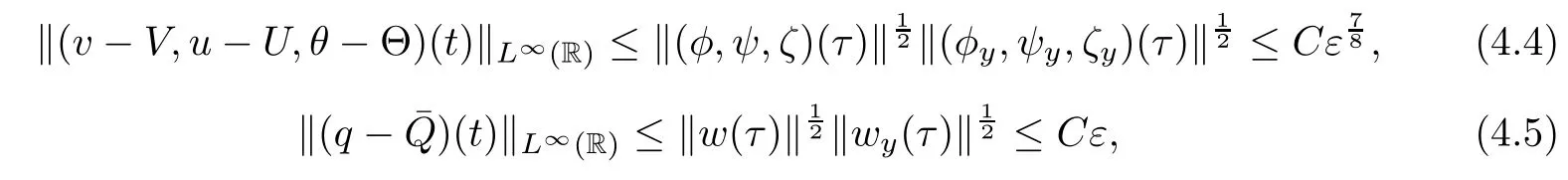
then(1.15)and(1.16)follows from(4.4),(1.9)and(4.5),(1.9),respectively.This completes the proof of Theorem 1.1.
References
[1]Lin C J,Coulombel J F,Goudon T.Shock pro fl ies for non-equilibrium radiating gases.Phys D,2006,218:83-94
[2]Lin C J,Coulombel J F,Goudon T.Asymptotic stability of shock pro fl ies in radiative hydrodynamics.C R Math Acad Sci Paris,2007,345:625-628
[3]Mihalas D,Mihalas B.Foundation of Radiation Hydrodynamics.London:Oxford University Press,1984
[4]Pomraning G C.The Equations of Radiation Hydrodynamics.New York:Pergamon Press,1973
[5]Vincenti W,Kruger C.Introduction to Physical Gas Dynamics.New York:Wiley,1965
[6]Kawashima S,Nishibata S.A singular limit for hyperbolic-parabolic coupled systems in radiation hydrodynamics.Indiana Univ Math J,2001,50:567-589
[7]Hamer K.Nonlinear effects on the propagation of sound waves in a radiating gas.Quart J Mech Appl Math,1971,24:155-168
[8]Serre D.Systems of Conservation Laws,Vol 1.Cambridge:Cambridge University Press,1999
[9]Smoller J.Shock Waves and Reaction-Di ff usion Equations.New York:Springer-Verlag,1994
[10]Atkinson F V,Peletier L A.Similarity solutions of the nonlinear di ff usion equation.Arch Rational Meth Anal,1974,54:373-392
[11]Duyn C J,Peletier L A.A class of similarity solutions of the nonlinear di ff usion equation.Nonlinear Anal,1976/77,1(3):223-233
[12]Wang J,Xie F.Singular limit to strong contact discontinuity for a 1D compressible radiation hydrodynamics model.SIAM J Math Anal,2011,43:1189-1204
[13]Rohde C,Wang W J,Xie F.Hyperbolic-Hyperbolic relaxation limit for a 1D compreesible radiation hydrodynamics model:superposition of rarefaction wave and contact wave.Commun Pure Appl Anal,2013,12:2145-2171
[14]Wang J,Xie F.Asymptotic stability of viscous contact wave for the 1D radiation hydrodynamics system,J Di ff er Equ,2011,251:1030-1055
[15]Xie F.Nonlinear stability of combination of viscous contact wave with rarefaction waves for a 1D radiation hydrodynamics model.Discrete Contin Dyn Syst Ser B,2012,17:1075-1100
[16]Rohde C,Xie F.Decay rates to viscous contact wave for a 1D compressible radiation hydrodynamics model.Math Models Methods Appl Sci,2013,23:441-469
[17]Ma S X.Zero dissipation limit to strong contact discontinuity for the 1-D compressible Navier-Stokes equations.J Di ff er Equ,2010,48:95-110
[18]Ma S X.Viscous limit to contact discontinuity for the 1-D compressible Navier-Stokes equations.J Math Anal Appl,2012,387:1033-1043
[19]Kawashima S,Nikkuni Y,Nishibata S.Larger-time behavior of solutions to hyperbolic-elliptic coupled systems.Arch Ration Mech Anal,2003,170:297-329
[20]Kawashima S,Nikkuni Y,Nishibata S.The initial value problem for hyperbolic-elliptic coupled systems and applications to radiation hydrodynamics//Analysis of Systems of Conservation Laws.Chapman and Hall/CRC,1997:87-127
[21]Kawashima S,Nishibata S.Weak solutions with a shock to a model system of the radiating gas.Sci Bull Josai Univ,1998,5:119-130
[22]Kawashima S,Nishibata S.Cauchy problem for a model system of the radiating gas:weak solutions with a jump and classical solutions.Math Models Methods Appl Sci,1999,9:69-91
[23]Kawashima S,Nishibata S.Shock waves for a model system of a radiating gas.SIAM J Math Anal,1999,30:95-117
[24]Lattanzio C,Marcati P.Golobal well-posedness and relaxation limits of a model for radiating gas.J Di ff er Equ,2003,190:439-465
[25]Lattanzio C,Mascia C,Serre D.Shock waves for radiative hyperbolic-elliptic systems.Indiana Univ Math J,2007,56:2601-2640
[26]Huang F M,Li M J,Wang Y.Zero dissipation limit to rarefaction wave with vacuum for the 1-D compressible Navier-Stokes equations.SIAM J Math Anal,2012,44:1742-1759
[27]Huang F M,Li X.Zero dissipation limit to rarefaction waves for the 1-D compressible Navier-Stokes equations.Chin Ann Math Ser B,2012,33:385-394
[28]Gao W L,Zhu C J.Asymptotic decay toward the planar rarefaction waves for a model system of the radiating gas in two dimensions.Math Models Methods Appl Sci,2008,18:511-541
[29]Gao W L,Ruan L Z,Zhu C J.Decay rates to the planar rarefaction waves for a model system of the radiating gas in n dimensions.J Di ff er Equ,2008,244:2614-2640
[30]Lin C J.Asymptotic stability of rarefaction waves in radiative hydrodynamics.Commun Math Sci,2011,9:207-223
[31]Xiao Q H,Liu Y N,Kim J S.Asymptotic behavior of rarefaction waves for a model system of a radiating gas.J Inequal Appl,2012,Art ID:81
[32]Nguyen T,Plaza R G,Zumbrun K.Stability of radiative shock profiles for hyperbolic-elliptic coupled systems.Phys D,2010,239:428-453
[33]Francesco M Di.Initial value problem and relaxation limits of the Hamer model for radiating gases in several space variables.NoDEA Nonlinear Di ff erential Equations Appl,2007,13:531-562
[34]Hong H,Huang F M.Asymptotic behavior of solutions toward the superposition of contout discontinuity and shock wave for compressible Navier-Stokes equations with free boundary.Acta Math Sci,2012,32B(1):389-412
[35]Xin Z P.Zero dissipation limit to rarefaction waves for the one-dimensional Navier-Stokes equations of compressible isentropic gases.Comm Pure Appl Math,1993,46:621-665
 Acta Mathematica Scientia(English Series)2016年1期
Acta Mathematica Scientia(English Series)2016年1期
- Acta Mathematica Scientia(English Series)的其它文章
- SOME STABILITY RESULTS FOR TIMOSHENKO SYSTEMS WITH COOPERATIVE FRICTIONAL AND INFINITE-MEMORY DAMPINGS IN THE DISPLACEMENT∗
- STABILITY OF VISCOUS SHOCK WAVES FOR THE ONE-DIMENSIONAL COMPRESSIBLE NAVIER-STOKES E QUATIONS WITH DENSITY-DEPENDENT VISCOSITY∗
- STABILITY ANALYSIS OF A COMPUTER VIRUS PROPAGATION MODEL WITH ANTIDOTE IN VULNERABLE SYSTEM∗
- STABILITY OF A PREDATOR-PREY SYSTEM WITH PREY TAXIS IN A GENERAL CLASS OF FUNCTIONAL RESPONSES∗
- NONSMOOTH CRITICAL POINT THEOREMS AND ITS APPLICATIONS TO QUASILINEAR SCHRÖDINGER EQUATIONS∗
- NORMAL FAMILIES OF MEROMORPHIC FUNCTIONS WITH SHARED VALUES∗
